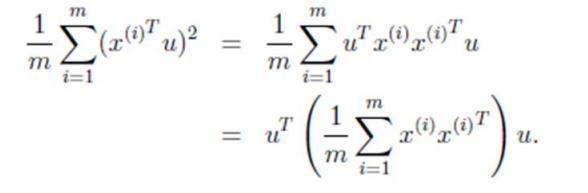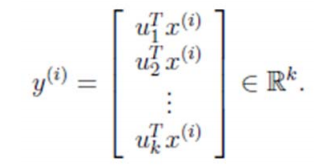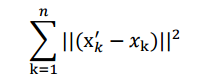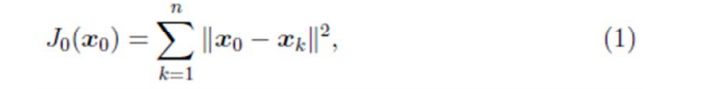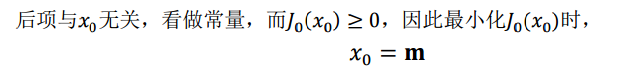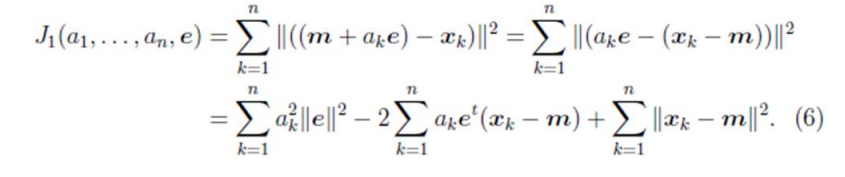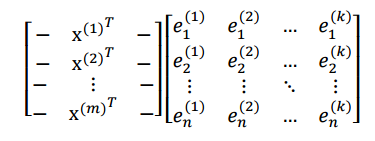要解釋為什麼協方差矩陣的特徵向量可以將原始特徵對映到 k 維理想特徵，我看到的有三個理論：分別是最大方差理論、最小錯誤理論和座標軸相關度理論。這裡簡單探討前兩種，最後一種在討論PCA 意義時簡單概述。

最大方差理論

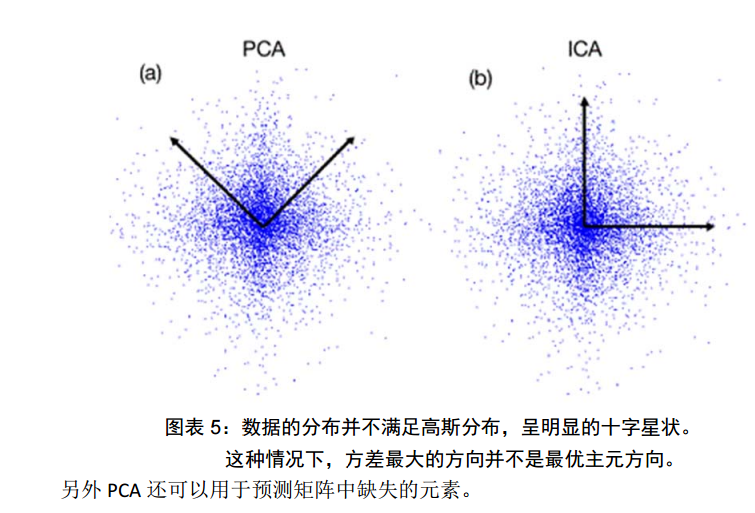
在訊號處理中認為訊號具有較大的方差，噪聲有較小的方差，信噪比就是訊號與噪聲的方差比，越大越好。如前面的圖，樣本在橫軸上的投影方差較大，在縱軸上的投影方差較小，那麼認為縱軸上的投影是由噪聲引起的。

因此我們認為，最好的 k 維特徵是將 n 維樣本點轉換為 k 維後，每一維上的樣本方差都很大。

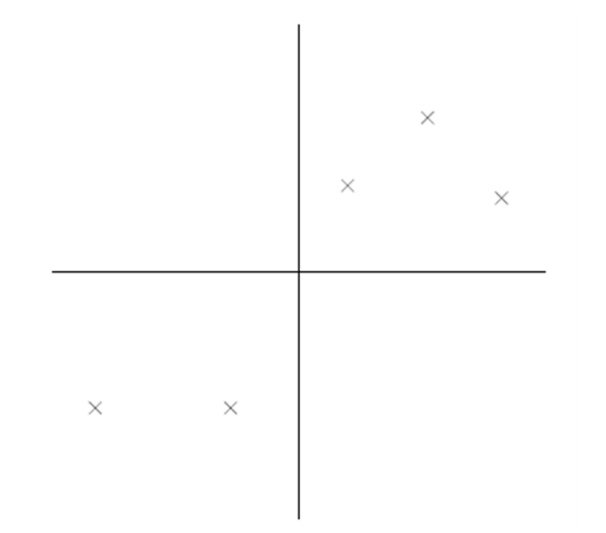
比如下圖有 5 個樣本點：（已經做過預處理，均值為 0，特徵方差歸一）

下面將樣本投影到某一維上，這裡用一條過原點的直線表示（之前預處理的過程實質是將原點移到樣本點的中心點）。

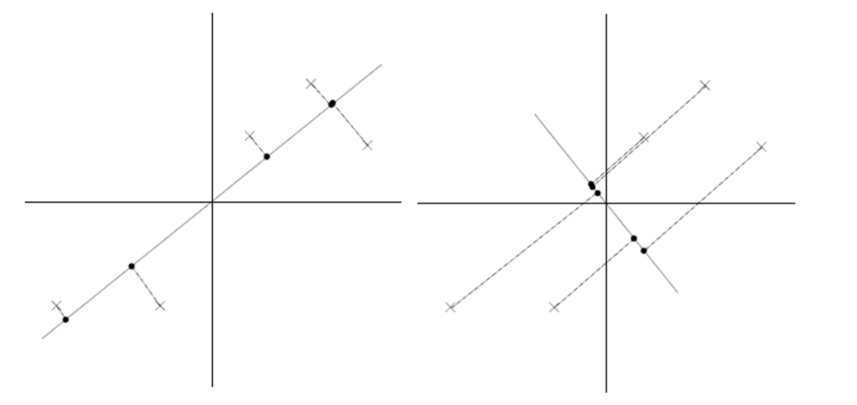
假設我們選擇兩條不同的直線做投影，那麼左右兩條中哪個好呢？根據我們之前的方差最大化理論，左邊的好，因為投影后的樣本點之間方差最大。

這裡先解釋一下投影的概念：

紅色點表示樣例x(i),藍色點表示x(i)在u上的投影，u是直線的斜率也是直線的方向向量，而且是單位向量。藍色點是x(i)在u上的投影點，離原點的距離是<x(i),u>（即x(i)Tu或uTx(i)）由於這些樣本點（樣例）的每一維特徵均值都為 0，因此投影到 u 上的樣本點（只有一個到原點的距離值）的均值仍然是 0。

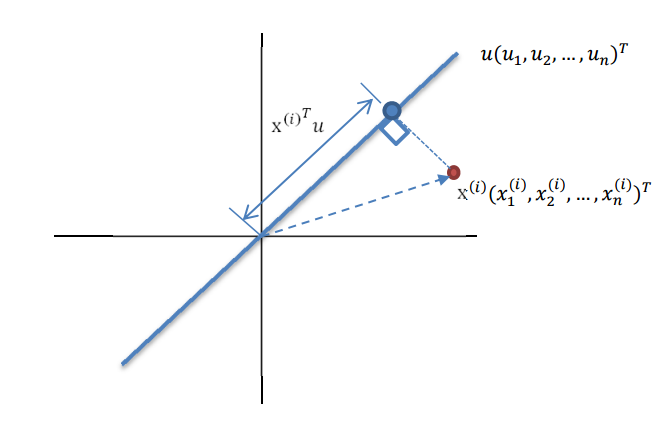
回到上面左右圖中的左圖，我們要求的是最佳的 u，使得投影后的樣本點方差最大。

由於投影后均值為 0，因此方差為：

中間那部分很熟悉啊，不就是樣本特徵的協方差矩陣麼(x(i)的均值為 0，一般協方差矩陣都除以 m‐1，這裡用 m）。

We got it！λ就是Σ的特徵值，u 是特徵向量。最佳的投影直線是特徵值λ最大時對應的特徵向量，其次是λ第二大對應的特徵向量，依次類推。

因此，我們只需要對協方差矩陣進行特徵值分解，得到的前 k 大特徵值對應的特徵向量就是最佳的 k 維新特徵，而且這 k 維新特徵是正交的。得到前 k 個 u 以後，樣例x(i)通過以下變換可以得到新的樣本:

通過選取最大的 k 個 u，使得方差較小的特徵（如噪聲）被丟棄。
這是其中一種對 PCA 的解釋，第二種是錯誤最小化。

最小平方誤差理論

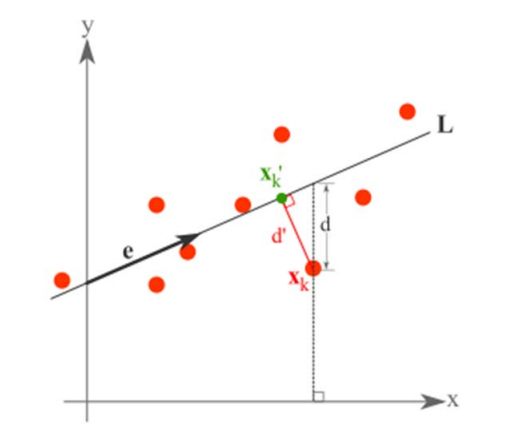
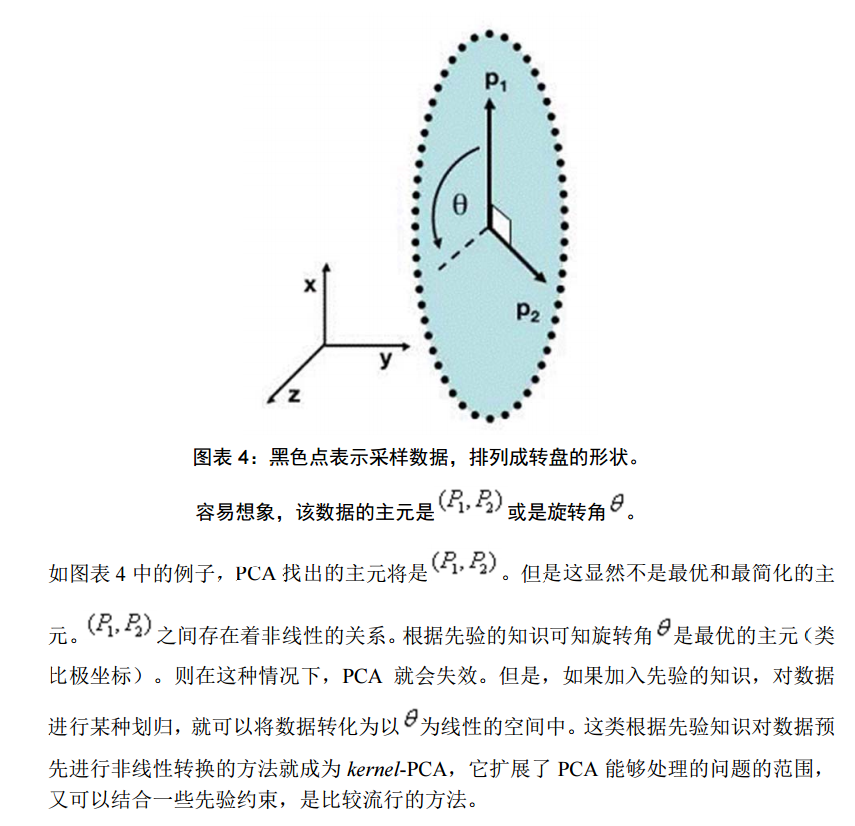
假設有這樣的二維樣本點（紅色點），回顧我們前面探討的是求一條直線，使得樣本點投影到直線上的點的方差最大。本質是求直線，那麼度量直線求的好不好，不僅僅只有方差最大化的方法。再回想我們最開始學習的線性迴歸等，目的也是求一個線性函式使得直線能夠最佳擬合樣本點，那麼我們能不能認為最佳的直線就是迴歸後的直線呢？迴歸時我們的最小二乘法度量的是樣本點到直線的座標軸距離。比如這個問題中，特徵是 x，類標籤是 y。迴歸時最小二乘法度量的是距離 d。如果使用迴歸方法來度量最佳直線，那麼就是直接在原始樣本上做迴歸了，跟特徵選擇就沒什麼關係了。

因此，我們打算選用另外一種評價直線好壞的方法，使用點到直線的距離 d’來度量。
現在有 n 個樣本點(x1,...,xn)，每個樣本點為 m 維（這節內容中使用的符號與上面的不太一致，需要重新理解符號的意義）。將樣本點xk在直線上的投影記為x′k，那麼我們就是要最小化

這個公式稱作最小平方誤差（Least Squared Error）。
而確定一條直線，一般只需要確定一個點以及方向即可。

第一步確定點：

假設要在空間中找一點x0來代表這 n 個樣本點，“代表”這個詞不是量化的，因此要量化成，我們就是要找一個 m 維的點x0，使得:

最小。其中J0(x0)是平方錯誤評價函式（squared‐error criterion function），假設 m 為 n個樣本點的均值：

那麼平方錯誤可以寫作：

第一行就類似座標系移動到以m為中心。

因此我們選取x0為樣本的均值m。

第二步確定方向：

我們首先固定 e，將其看做是常量，||e||=1，然後對ak進行求導，得:

這個結果意思是說，如果知道了 e，那麼將x′k−m與e做內積，就可以得到xk在e上的投影到m的距離。

兩邊除以 n‐1 就變成了，對協方差矩陣求特徵值向量了。

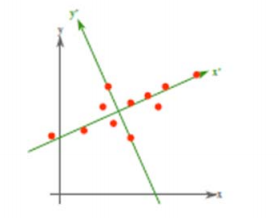
從不同的思路出發，最後得到同一個結果，對協方差矩陣求特徵向量，求得後特徵向量上就成為了新的座標，如下圖：

這時候點都聚集在新的座標軸周圍，因為我們使用的最小平方誤差的意義就在此。

PCA 理論意義

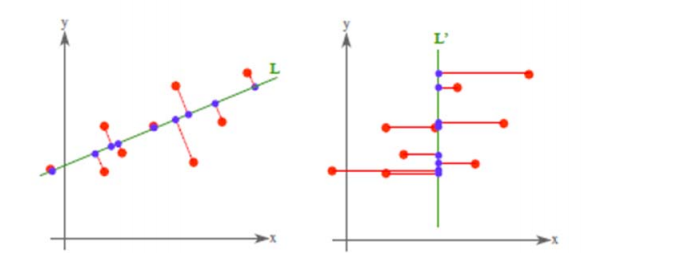
PCA 將 n 個特徵降維到 k 個，可以用來進行資料壓縮，如果 100 維的向量最後可以用10 維來表示，那麼壓縮率為 90%。同樣影象處理領域的 KL 變換使用 PCA 做影象壓縮。但PCA 要保證降維後，還要保證資料的特性損失最小。再看回顧一下 PCA 的效果。經過 PCA處理後，二維資料投影到一維上可以有以下幾種情況：

我們認為左圖好，一方面是投影后方差最大，一方面是點到直線的距離平方和最小，而且直線過樣本點的中心點。為什麼右邊的投影效果比較差？直覺是因為座標軸之間相關，以至於去掉一個座標軸，就會使得座標點無法被單獨一個座標軸確定。

PCA 得到的 k 個座標軸實際上是 k 個特徵向量，由於協方差矩陣對稱，因此 k 個特徵向量正交。看下面的計算過程。

我們最後得到的投影結果是AE，E 是 k 個特徵向量組成的矩陣，展開如下：

得到的新的樣例矩陣就是 m 個樣例到 k 個特徵向量的投影，也是這 k 個特徵向量的線性組合。。e 之間是正交的。從矩陣乘法中可以看出，PCA 所做的變換是將原始樣本點（n 維），投影到 k 個正交的座標系中去，丟棄其他維度的資訊。
舉個例子，假設宇宙是 n 維的（霍金說是 13 維的），我們得到銀河系中每個星星的座標（相對於銀河系中心的 n 維向量），然而我們想用二維座標去逼近這些樣本點，假設算出來的協方差矩陣的特徵向量分別是圖中的水平和豎直方向，那麼我們建議以銀河系中心為原點的 x 和 y 座標軸，所有的星星都投影到 x和 y 上，得到下面的圖片。然而我們丟棄了每個星星離我們的遠近距離等資訊。

總結與討論

∙PCA 技術的一大好處是對資料進行降維的處理。我們可以對新求出的“主元”向量的重要性進行排序，根據需要取前面最重要的部分，將後面的維數省去，可以達到降維從而簡化模型或是對資料進行壓縮的效果。同時最大程度的保持了原有資料的資訊。
∙PCA 技術的一個很大的優點是，它是完全無引數限制的。在 PCA 的計算過程中完全不需要人為的設定引數或是根據任何經驗模型對計算進行干預，最後的結果只與資料相關，與使用者是獨立的。
但是，這一點同時也可以看作是缺點。如果使用者對觀測物件有一定的先驗知識，掌握了資料的一些特徵，卻無法通過引數化等方法對處理過程進行干預，可能會得不到預期的效果，效率也不高。

其他參考文獻

下面的練習來自UFLDL
pca2d

close all

%%================================================================
%% Step 0: Load data
%  We have provided the code to load data from pcaData.txt into x.
%  x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to
%  the kth data point.Here we provide the code to load natural image data into x.
%  You do not need to change the code below.

x = load('pcaData.txt','-ascii');
figure(1);
scatter(x(1, :), x(2, :));
title('Raw data');


%%================================================================
%% Step 1a: Implement PCA to obtain U 
%  Implement PCA to obtain the rotation matrix U, which is the eigenbasis
%  sigma. 

% -------------------- YOUR CODE HERE -------------------- 
u = zeros(size(x, 1)); % You need to compute this
avg = mean(x,2);
x = x - repmat(avg,1,size(x,2));
sigma = x * x' /size(x,2);
[U,S,V] = svd(sigma);
u = U;
% -------------------------------------------------------- 
hold on
plot([0 u(1,1)], [0 u(2,1)]);
plot([0 u(1,2)], [0 u(2,2)]);
scatter(x(1, :), x(2, :));
hold off

%%================================================================
%% Step 1b: Compute xRot, the projection on to the eigenbasis
%  Now, compute xRot by projecting the data on to the basis defined
%  by U. Visualize the points by performing a scatter plot.

% -------------------- YOUR CODE HERE -------------------- 
xRot = zeros(size(x)); % You need to compute this
xRot = u'*x;

% -------------------------------------------------------- 

% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure(2);
scatter(xRot(1, :), xRot(2, :));
title('xRot');

%%================================================================
%% Step 2: Reduce the number of dimensions from 2 to 1. 
%  Compute xRot again (this time projecting to 1 dimension).
%  Then, compute xHat by projecting the xRot back onto the original axes 
%  to see the effect of dimension reduction

% -------------------- YOUR CODE HERE -------------------- 
k = 1; % Use k = 1 and project the data onto the first eigenbasis
xHat = zeros(size(x)); % You need to compute this
x_pca = u(:,1)' * x;
xHat = U*[x_pca;zeros(1,size(x,2))];


% -------------------------------------------------------- 
figure(3);
scatter(xHat(1, :), xHat(2, :));
title('xHat');


%%================================================================
%% Step 3: PCA Whitening
%  Complute xPCAWhite and plot the results.

epsilon = 1e-5;
% -------------------- YOUR CODE HERE -------------------- 
xPCAWhite = zeros(size(x)); % You need to compute this

xPCAWhite = diag( 1./sqrt(diag(S)+epsilon) ) * xRot;


% -------------------------------------------------------- 
figure(4);
scatter(xPCAWhite(1, :), xPCAWhite(2, :));
title('xPCAWhite');

%%================================================================
%% Step 3: ZCA Whitening
%  Complute xZCAWhite and plot the results.

% -------------------- YOUR CODE HERE -------------------- 
xZCAWhite = zeros(size(x)); % You need to compute this
xZCAWhite = U * xPCAWhite;

% -------------------------------------------------------- 
figure(5);
scatter(xZCAWhite(1, :), xZCAWhite(2, :));
title('xZCAWhite');

%% Congratulations! When you have reached this point, you are done!
%  You can now move onto the next PCA exercise. :)

pca_gen

%%================================================================
%% Step 0a: Load data
%  Here we provide the code to load natural image data into x.
%  x will be a 144 * 10000 matrix, where the kth column x(:, k) corresponds to
%  the raw image data from the kth 12x12 image patch sampled.
%  You do not need to change the code below.

x = sampleIMAGESRAW();
figure('name','Raw images');
randsel = randi(size(x,2),200,1); % A random selection of samples for visualization
display_network(x(:,randsel));%這裡只顯示了部分子樣本

%%================================================================
%% Step 0b: Zero-mean the data (by row)
%  You can make use of the mean and repmat/bsxfun functions.

% -------------------- YOUR CODE HERE -------------------- 
[n,m] = size(x)  %n是屬性，m是樣本數
avg_features = mean(x,2) %求得每一維特徵的均值  2代表按行求均值
x = x - repmat(avg_features, 1, size(x,2));
display_network(x(:,randsel));%做0均值前後的對比

%%================================================================
%% Step 1a: Implement PCA to obtain xRot
%  Implement PCA to obtain xRot, the matrix in which the data is expressed
%  with respect to the eigenbasis of sigma, which is the matrix U.


% -------------------- YOUR CODE HERE -------------------- 
xRot = zeros(size(x)); % You need to compute this
sigma = x*x'/size(x,2);
[U,S,V] = svd(sigma)%計算特徵向量 U特徵向量構成的矩陣，特徵向量數與屬性數相同，第一個特徵向量與某個樣本相乘解a1*x1得xRot中樣本x1的第一個屬性，S特徵值
xRot = U' * x; 
%%================================================================
%% Step 1b: Check your implementation of PCA
%  The covariance matrix for the data expressed with respect to the basis U
%  should be a diagonal matrix with non-zero entries only along the main
%  diagonal. We will verify this here.
%  Write code to compute the covariance matrix, covar. 
%  When visualised as an image, you should see a straight line across the
%  diagonal (non-zero entries) against a blue background (zero entries).

% -------------------- YOUR CODE HERE -------------------- 
covar = zeros(size(x, 1)); % You need to compute this
covar = xRot*xRot';%協方差是屬性間的協方差，不是每個樣本的協方差
% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure('name','Visualisation of covariance matrix');
imagesc(covar);

%%================================================================
%% Step 2: Find k, the number of components to retain
%  Write code to determine k, the number of components to retain in order
%  to retain at least 99% of the variance.

% -------------------- YOUR CODE HERE -------------------- 
k = 0; % Set k accordingly
var_sum = sum(diag(covar));%covar主對角線上就是特徵值
curr_var_sum = 0;
for i = 1:length(covar)
   curr_var_sum = curr_var_sum + covar(i,i); 
   if curr_var_sum / var_sum >= 0.99
       k=i;
       break;
   end
end

%%================================================================
%% Step 3: Implement PCA with dimension reduction
%  Now that you have found k, you can reduce the dimension of the data by
%  discarding the remaining dimensions. In this way, you can represent the
%  data in k dimensions instead of the original 144, which will save you
%  computational time when running learning algorithms on the reduced
%  representation.
% 
%  Following the dimension reduction, invert the PCA transformation to produce 
%  the matrix xHat, the dimension-reduced data with respect to the original basis.
%  Visualise the data and compare it to the raw data. You will observe that
%  there is little loss due to throwing away the principal components that
%  correspond to dimensions with low variation.

% -------------------- YOUR CODE HERE -------------------- 
xHat = zeros(size(x));  % You need to compute this
xTitle = U(:,1:k)' * x; %這個是pca降維後的結果
xHat = U*[xTitle;zeros(n-k,m)];%由pca後的資料恢復原圖

% Visualise the data, and compare it to the raw data
% You should observe that the raw and processed data are of comparable quality.
% For comparison, you may wish to generate a PCA reduced image which
% retains only 90% of the variance.

figure('name',['PCA processed images ',sprintf('(%d / %d dimensions)', k, size(x, 1)),'']);
display_network(xHat(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));

%%================================================================
%% Step 4a: Implement PCA with whitening and regularisation
%  Implement PCA with whitening and regularisation to produce the matrix
%  xPCAWhite. 

epsilon = 0.1;
xPCAWhite = zeros(size(x));

% -------------------- YOUR CODE HERE -------------------- 
xPCAWhite = diag(1./sqrt(diag(S) + epsilon)) * xRot;
%%================================================================
%% Step 4b: Check your implementation of PCA whitening 
%  Check your implementation of PCA whitening with and without regularisation. 
%  PCA whitening without regularisation results a covariance matrix 
%  that is equal to the identity matrix. PCA whitening with regularisation
%  results in a covariance matrix with diagonal entries starting close to 
%  1 and gradually becoming smaller. We will verify these properties here.
%  Write code to compute the covariance matrix, covar. 
%
%  Without regularisation (set epsilon to 0 or close to 0), 
%  when visualised as an image, you should see a red line across the
%  diagonal (one entries) against a blue background (zero entries).
%  With regularisation, you should see a red line that slowly turns
%  blue across the diagonal, corresponding to the one entries slowly
%  becoming smaller.

% -------------------- YOUR CODE HERE -------------------- 
covar = xPCAWhite * xPCAWhite';
% Visualise the covariance matrix. You should see a red line across the
% diagonal against a blue background.
figure('name','Visualisation of covariance matrix');
imagesc(covar);

%%================================================================
%% Step 5: Implement ZCA whitening
%  Now implement ZCA whitening to produce the matrix xZCAWhite. 
%  Visualise the data and compare it to the raw data. You should observe
%  that whitening results in, among other things, enhanced edges.

xZCAWhite = zeros(size(x));%ZCA白化一般都作用於所有維度，資料不降維
xZCAWhite = U * xPCAWhite; %ZCA其實就是做了PCA白化後再復原原圖---增強邊緣
% -------------------- YOUR CODE HERE -------------------- 

% Visualise the data, and compare it to the raw data.
% You should observe that the whitened images have enhanced edges.
figure('name','ZCA whitened images');
display_network(xZCAWhite(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));

使用pca的基本步驟是
輸入x—對x做零均值—計算x的協方差矩陣—計算特徵值特徵向量—-白化（可選，它可消除樣本間的相關性）—-選取前k個特徵向量