主成分分析（Principal components analysis，以下簡稱PCA）是最重要的降維方法之一。在資料壓縮消除冗餘和資料噪音消除等領域都有廣泛的應用。一般我們提到降維最容易想到的演算法就是PCA，下面我們就對PCA的原理做一個總結。

1. PCA的思想

　　　　PCA顧名思義，就是找出資料裡最主要的方面，用資料裡最主要的方面來代替原始資料。具體的，假如我們的資料集是n維的，共有m個數據$(x^{(1)},x^{(2)},...,x^{(m)})$。我們希望將這m個數據的維度從n維降到n'維，希望這m個n'維的資料集儘可能的代表原始資料集。我們知道資料從n維降到n'維肯定會有損失，但是我們希望損失儘可能的小。那麼如何讓這n'維的資料儘可能表示原來的資料呢？

　　　　我們先看看最簡單的情況，也就是n=2，n'=1,也就是將資料從二維降維到一維。資料如下圖。我們希望找到某一個維度方向，它可以代表這兩個維度的資料。圖中列了兩個向量方向，$u_1$和$u_2$，那麼哪個向量可以更好的代表原始資料集呢？從直觀上也可以看出，$u_1$比$u_2$好。

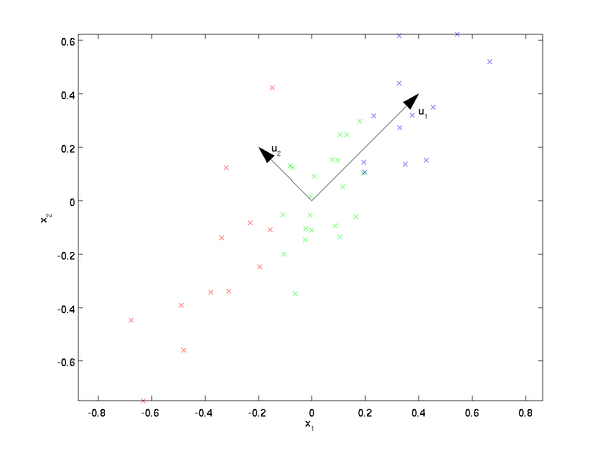
　　　　為什麼$u_1$比$u_2$好呢？可以有兩種解釋，第一種解釋是樣本點到這個直線的距離足夠近，第二種解釋是樣本點在這個直線上的投影能儘可能的分開。

　　　　假如我們把n'從1維推廣到任意維，則我們的希望降維的標準為：樣本點到這個超平面的距離足夠近,或者說樣本點在這個超平面上的投影能儘可能的分開。

　　　　基於上面的兩種標準，我們可以得到PCA的兩種等價推導。

2. PCA的推導:基於最小投影距離

　　　　我們首先看第一種解釋的推導，即樣本點到這個超平面的距離足夠近。

　　　　假設m個n維資料$(x^{(1)}, x^{(2)},...,x^{(m)})$都已經進行了中心化，即$\sum\limits_{i=1}^{m}x^{(i)}=0$。經過投影變換後得到的新座標系為$\{w_1,w_2,...,w_n\}$,其中$w$是標準正交基，即$||w||_2=1, w_i^Tw_j=0$。

　　　　如果我們將資料從n維降到n'維，即丟棄新座標系中的部分座標，則新的座標系為$\{w_1,w_2,...,w_{n'}\}$,樣本點$x^{(i)}$在n'維座標系中的投影為：$z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})^T$.其中，$z_j^{(i)} = w_j^Tx^{(i)}$是$x^{(i)}$在低維座標系裡第j維的座標。

　　　　如果我們用$z^{(i)}$來恢復原始資料$x^{(i)}$,則得到的恢復資料$\overline{x}^{(i)} = \sum\limits_{j=1}^{n'}z_j^{(i)}w_j = Wz^{(i)}$,其中，W為標準正交基組成的矩陣。

　　　　現在我們考慮整個樣本集，我們希望所有的樣本到這個超平面的距離足夠近，即最小化下式：$$\sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2$$

　　　　將這個式子進行整理，可以得到:

$$ \begin{align} \sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 & = \sum\limits_{i=1}^{m}|| Wz^{(i)} - x^{(i)}||_2^2 \\& = \sum\limits_{i=1}^{m}(Wz^{(i)})^T(Wz^{(i)}) - 2\sum\limits_{i=1}^{m}(Wz^{(i)})^Tx^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}W^Tx^{(i)} +\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}z^{(i)}+\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}  \\& = - \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}  \\& =   -tr( W^T（\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T})W)  + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& =  -tr( W^TXX^TW)  + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}  \end{align}$$

　　　　其中第（1）步用到了$\overline{x}^{(i)}=Wz^{(i)} $,第二步用到了平方和展開，第（3）步用到了矩陣轉置公式$(AB)^T =B^TA^T$和$W^TW=I$,第（4）步用到了$z^{(i)}=W^Tx^{(i)}$，第（5）步合併同類項，第（6）步用到了$z^{(i)}=W^Tx^{(i)}$和矩陣的跡,第7步將代數和表達為矩陣形式。

　　　　注意到$\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}$是資料集的協方差矩陣，W的每一個向量$w_j$是標準正交基。而$\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}$是一個常量。最小化上式等價於：$$\underbrace{arg\;min}_{W}\;-tr( W^TXX^TW) \;\;s.t. W^TW=I$$

　　　　這個最小化不難，直接觀察也可以發現最小值對應的W由協方差矩陣$XX^T$最大的n'個特徵值對應的特徵向量組成。當然用數學推導也很容易。利用拉格朗日函式可以得到$$J(W) = -tr( W^TXX^TW + \lambda(W^TW-I))$$

　　　　對W求導有$-XX^TW+\lambda W=0$, 整理下即為：$$XX^TW=\lambda W$$

　　　　這樣可以更清楚的看出，W為$XX^T$的n'個特徵向量組成的矩陣，而$\lambda$為$XX^T$的若干特徵值組成的矩陣，特徵值在主對角線上，其餘位置為0。當我們將資料集從n維降到n'維時，需要找到最大的n'個特徵值對應的特徵向量。這n'個特徵向量組成的矩陣W即為我們需要的矩陣。對於原始資料集，我們只需要用$z^{(i)}=W^Tx^{(i)}$,就可以把原始資料集降維到最小投影距離的n'維資料集。

　　　　如果你熟悉譜聚類的優化過程，就會發現和PCA的非常類似，只不過譜聚類是求前k個最小的特徵值對應的特徵向量，而PCA是求前k個最大的特徵值對應的特徵向量。　　

3. PCA的推導:基於最大投影方差

　　　　現在我們再來看看基於最大投影方差的推導。

假設m個n維資料$(x^{(1)}, x^{(2)},...,x^{(m)})$都已經進行了中心化，即$\sum\limits_{i=1}^{m}x^{(i)}=0$。經過投影變換後得到的新座標系為$\{w_1,w_2,...,w_n\}$,其中$w$是標準正交基，即$||w||_2=1, w_i^Tw_j=0$。

　　　　如果我們將資料從n維降到n'維，即丟棄新座標系中的部分座標，則新的座標系為$\{w_1,w_2,...,w_{n'}\}$,樣本點$x^{(i)}$在n'維座標系中的投影為：$z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})^T$.其中，$z_j^{(i)} = w_j^Tx^{(i)}$是$x^{(i)}$在低維座標系裡第j維的座標。

　　　　對於任意一個樣本$x^{(i)}$，在新的座標系中的投影為$W^Tx^{(i)}$,在新座標系中的投影方差為$W^Tx^{(i)}x^{(i)T}W$，要使所有的樣本的投影方差和最大，也就是最大化$ \sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W$的跡,即：$$\underbrace{arg\;max}_{W}\;tr( W^TXX^TW) \;\;s.t. W^TW=I$$

　　　　觀察第二節的基於最小投影距離的優化目標，可以發現完全一樣，只是一個是加負號的最小化，一個是最大化。

　　　　利用拉格朗日函式可以得到$$J(W) = tr( W^TXX^TW + \lambda(W^TW-I))$$

　　　　對W求導有$XX^TW+\lambda W=0$, 整理下即為：$$XX^TW=（-\lambda）W$$

　　　　和上面一樣可以看出，W為$XX^T$的n'個特徵向量組成的矩陣，而$-\lambda$為$XX^T$的若干特徵值組成的矩陣，特徵值在主對角線上，其餘位置為0。當我們將資料集從n維降到n'維時，需要找到最大的n'個特徵值對應的特徵向量。這n'個特徵向量組成的矩陣W即為我們需要的矩陣。對於原始資料集，我們只需要用$z^{(i)}=W^Tx^{(i)}$,就可以把原始資料集降維到最小投影距離的n'維資料集。

4. PCA演算法流程

　　　　從上面兩節我們可以看出，求樣本$x^{(i)}$的n'維的主成分其實就是求樣本集的協方差矩陣$XX^T$的前n'個特徵值對應特徵向量矩陣W，然後對於每個樣本$x^{(i)}$,做如下變換$z^{(i)}=W^Tx^{(i)}$，即達到降維的PCA目的。

　　　　下面我們看看具體的演算法流程。

　　　　輸入：n維樣本集$D=(x^{(1)}, x^{(2)},...,x^{(m)})$，要降維到的維數n'.

　　　　輸出：降維後的樣本集$D'$

　　　　1) 對所有的樣本進行中心化： $x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$

　　　　2) 計算樣本的協方差矩陣$XX^T$

　　　　3) 對矩陣$XX^T$進行特徵值分解

　　　　4）取出最大的n'個特徵值對應的特徵向量$(w_1,w_2,...,w_{n'})$, 將所有的特徵向量標準化後，組成特徵向量矩陣W。

　　　　5）對樣本集中的每一個樣本$x^{(i)}$,轉化為新的樣本$z^{(i)}=W^Tx^{(i)}$

　　　　6) 得到輸出樣本集$D' =(z^{(1)}, z^{(2)},...,z^{(m)})$

　　　　有時候，我們不指定降維後的n'的值，而是換種方式，指定一個降維到的主成分比重閾值t。這個閾值t在（0,1]之間。假如我們的n個特徵值為$\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n$,則n'可以通過下式得到:$$\frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq t $$

5. PCA例項

　　　　下面舉一個簡單的例子，說明PCA的過程。

　　　　假設我們的資料集有10個二維資料(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)，需要用PCA降到1維特徵。

　　　　首先我們對樣本中心化，這裡樣本的均值為(1.81, 1.91),所有的樣本減去這個均值後，即中心化後的資料集為(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。

　　　　現在我們開始求樣本的協方差矩陣，由於我們是二維的，則協方差矩陣為：

$$\mathbf{XX^T} =
\left( \begin{array}{ccc}
cov(x_1,x_1) & cov(x_1,x_2)\\  
cov(x_2,x_1) & cov(x_2,x_2) \end{array} \right)$$

　　　　對於我們的資料，求出協方差矩陣為：

$$\mathbf{XX^T} =
\left( \begin{array}{ccc}
0.616555556 & 0.615444444\\  
0.615444444 & 0.716555556 \end{array} \right)$$

　　　　求出特徵值為（0.490833989， 1.28402771），對應的特徵向量分別為：$(0.735178656, 0.677873399)^T\;\; (-0.677873399, -0.735178656)^T$,由於最大的k=1個特徵值為1.28402771，對於的k=1個特徵向量為$(-0.677873399, -0.735178656)^T$. 則我們的W=$(-0.677873399, -0.735178656)^T$

　　　　我們對所有的資料集進行投影$z^{(i)}=W^Tx^{(i)}$，得到PCA降維後的10個一維資料集為：(-0.827970186， 1.77758033， -0.992197494， -0.274210416， -1.67580142， -0.912949103， 0.0991094375， 1.14457216, 0.438046137， 1.22382056)

6. 核主成分分析KPCA介紹

　　　　在上面的PCA演算法中，我們假設存在一個線性的超平面，可以讓我們對資料進行投影。但是有些時候，資料不是線性的，不能直接進行PCA降維。這裡就需要用到和支援向量機一樣的核函式的思想，先把資料集從n維對映到線性可分的高維N>n,然後再從N維降維到一個低維度n', 這裡的維度之間滿足n'<n<N。

　　　　使用了核函式的主成分分析一般稱之為核主成分分析(Kernelized PCA, 以下簡稱KPCA。假設高維空間的資料是由n維空間的資料通過對映$\phi$產生。

　　　　則對於n維空間的特徵分解：$$ \sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}W=\lambda W$$

　　　　對映為：$$ \sum\limits_{i=1}^{m}\phi(x^{(i)})\phi(x^{(i)})^TW=\lambda W$$

　　　　通過在高維空間進行協方差矩陣的特徵值分解，然後用和PCA一樣的方法進行降維。一般來說，對映$\phi$不用顯式的計算，而是在需要計算的時候通過核函式完成。由於KPCA需要核函式的運算，因此它的計算量要比PCA大很多。

7. PCA演算法總結

　　　　這裡對PCA演算法做一個總結。作為一個非監督學習的降維方法，它只需要特徵值分解，就可以對資料進行壓縮，去噪。因此在實際場景應用很廣泛。為了克服PCA的一些缺點，出現了很多PCA的變種，比如第六節的為解決非線性降維的KPCA，還有解決記憶體限制的增量PCA方法Incremental PCA，以及解決稀疏資料降維的PCA方法Sparse PCA等。

　　　　PCA演算法的主要優點有：

　　　　1）僅僅需要以方差衡量資訊量，不受資料集以外的因素影響。　

　　　　2）各主成分之間正交，可消除原始資料成分間的相互影響的因素。

　　　　3）計算方法簡單，主要運算是特徵值分解，易於實現。

　　　　PCA演算法的主要缺點有：

　　　　1）主成分各個特徵維度的含義具有一定的模糊性，不如原始樣本特徵的解釋性強。

　　　　2）方差小的非主成分也可能含有對樣本差異的重要資訊，因降維丟棄可能對後續資料處理有影響。

祝大家新年快樂！

（歡迎轉載，轉載請註明出處。歡迎溝通交流： [email protected]）