題目：

Garland

Time Limit: 1000MS	Memory Limit: 10000K
Total Submissions: 2778	Accepted: 1170

Description

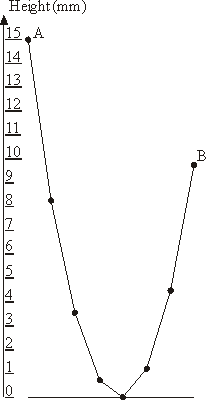The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps. 

The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground. 

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations: 

H1 = A 
Hi = (H_i-1 + H_i+1)/2 - 1, for all 1 < i < N 
HN = B 
Hi >= 0, for all 1 <= i <= N 

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75. 

Input

The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.

Output

Write to the output file the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.

題意：有N個燈，第一個燈的高度是a，第2個到第（n-1）個燈的高度值都滿足：Hi =（H i-1 + H i + 1）/ 2-1 的的關係，求第N個燈的最低高度，使這n個燈的高度都 >= 0。

思路：這題是不能二分答案的，因為這樣無論如何都無法進行遞推，找到最低的位置。

我們將題目給的式子稍加變動得：h（i+1） = 2*h（i）- h（i-1）+ 2 。（1式子）則發現由前兩個燈的高度可以推出第3個燈的高度。

又因為：h（i+2） = 2*h（i+1）- h（i）+ 2  ，    把1式子帶入 得：        h（i+2） = 3*h（i）- 2*h（i-1）+ 6。（2式子）

又因為：h（i+3） = 2*h（i+2）- h（i+1）+ 2 ，把1式子2式子代入 得：h（i+3） = 4*h（i）- 3*h（i-1）+ 12。（3式子）

又因為：h（i+4） = 2*h（i+3）- h（i+2）+ 2 ，把2式子3式子代入 得：h（i+4） = 5*h（i）- 4*h（i-1）+ 20。（4式子）

又因為……

然後我們得到了h（i+n） = （n+1）*h（i）- n*h（i-1）+ n*(n+1)。 令i-1 = 1，則i==2.（同時使i+n == N）我們可以發現，第N個燈的高度(也就是答案)與第2個燈的高度成正相關。

於是我們就可以二分第2個燈的高度，然後遞推判斷是否可行，和求第n個燈的高度了。

程式碼：

#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<set>
#define sd(x) scanf("%d",&x)
#define ss(x) scanf("%s",x)
#define sc(x) scanf("%c",&x)
#define sf(x) scanf("%f",&x)
#define slf(x) scanf("%lf",&x)
#define slld(x) scanf("%lld",&x)
#define me(x,b) memset(x,b,sizeof(x))
#define pd(d) printf("%d\n",d);
#define plld(d) printf("%lld\n",d);
#define eps 1.0E-8
// #define Reast1nPeace

typedef long long ll;

using namespace std;

const int INF = 0x3f3f3f3f;

double a;
int n;
double ans;
double t[1010];

bool judge(double x){
	t[1] = a;
	t[2] = x;
	for(int i = 3 ; i<=n ; i++){
		t[i] = 2*t[i-1] - t[i-2] + 2;
		if(t[i]<0){
			return false;
		}
	}
	ans = t[n];
	return true;
}

int main(){
#ifdef Reast1nPeace
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	ios::sync_with_stdio(false);
	cin>>n>>a;
	
	double l = 0 ; double r = INF;
	for(int i = 0 ; i<100 ; i++){
		double mid = (l+r)/2;
		if(judge(mid)){
			r = mid;
		}
		else{
			l = mid;
		}
	}
	printf("%.2lf\n",ans);
	return 0;
}