資料降維基本原理是將樣本點從輸入空間通過線性或非線性變換對映到一個低維空間，從而獲得一個關於原資料集緊緻的低維表示。

資料降維工具箱drtoolbox中眾多演算法，這裡簡單做個分類。

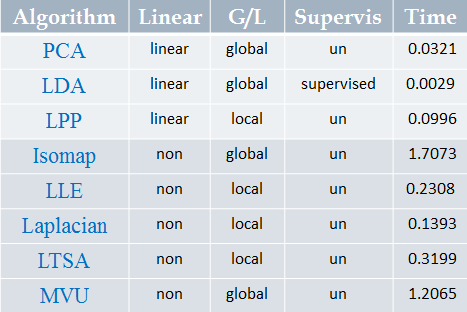
因為很多並沒有仔細瞭解，在此次只對八種方法做分類：主成分分析（Principal Component Analysis,PCA)、線性判別分析（Linear Discriminant Analysis,LDA）、等距對映（Isomap）、區域性線性嵌入（Locally Linear Embedding,LLE）、Laplacian 特徵對映（Laplacian Eigenmaps）、區域性保留投影（Local Preserving Projection,LPP）、區域性切空間排列（Local Tangent Space Alignment,LTSA）、最大方差展開（ Maximum Variance Unfolding,MVU）

線性/非線性

線性降維是指通過降維所得到的低維資料能保持高維資料點之間的線性關係。線性降維方法主要包括PCA、LDA、LPP（LPP其實是Laplacian Eigenmaps的線性表示）；非線性降維一類是基於核的，如KPCA，此處暫不討論；另一類就是通常所說的流形學習：從高維取樣資料中恢復出低維流形結構（假設資料是均勻取樣於一個高維歐式空間中的低維流形），即找到高維空間中的低維流形，並求出相應的嵌入對映。非線性流形學習方法有：Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU 整體來說，線性方法計算塊，複雜度低，但對複雜的資料降維效果較差。

監督/非監督

監督式和非監督式學習的主要區別在於資料樣本是否存在類別資訊。非監督降維方法的目標是在降維時使得資訊的損失最小，如PCA、LPP、Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU；監督式降維方法的目標是最大化類別間的辨別信，如LDA。事實上，對於非監督式降維演算法，都有相應的監督式或半監督式方法的研究。

全域性/區域性

區域性方法僅考慮樣品集合的區域性資訊，即資料點與臨近點之間的關係。區域性方法以LLE為代表，還包括Laplacian Eigenmaps、LPP、LTSA。 全域性方法不僅考慮樣本幾何的區域性資訊，和考慮樣本集合的全域性資訊，及樣本點與非臨近點之間的關係。全域性演算法有PCA、LDA、Isomap、MVU。 由於區域性方法並不考慮資料流形上相距較遠的樣本之間的關係，因此，區域性方法無法達到“使在資料流形上相距較遠的樣本的特徵也相距較遠”的目的。
以下是對一組三維資料（900樣本）降到一維，應用八種演算法的時間對比：