https://kayhan.dbmi.pitt.edu/sites/default/files/lecture2.pdf

 P(sequence) given both dices are fair

             x2    →    x4

      ↗                             ↘

 x1                                        x5

      ↘                     ↗

             x3          

P(x5) = P(X1) P(X2|X1)  P(X3|X1)  P(X4|X2) P(X5|X3,X4)

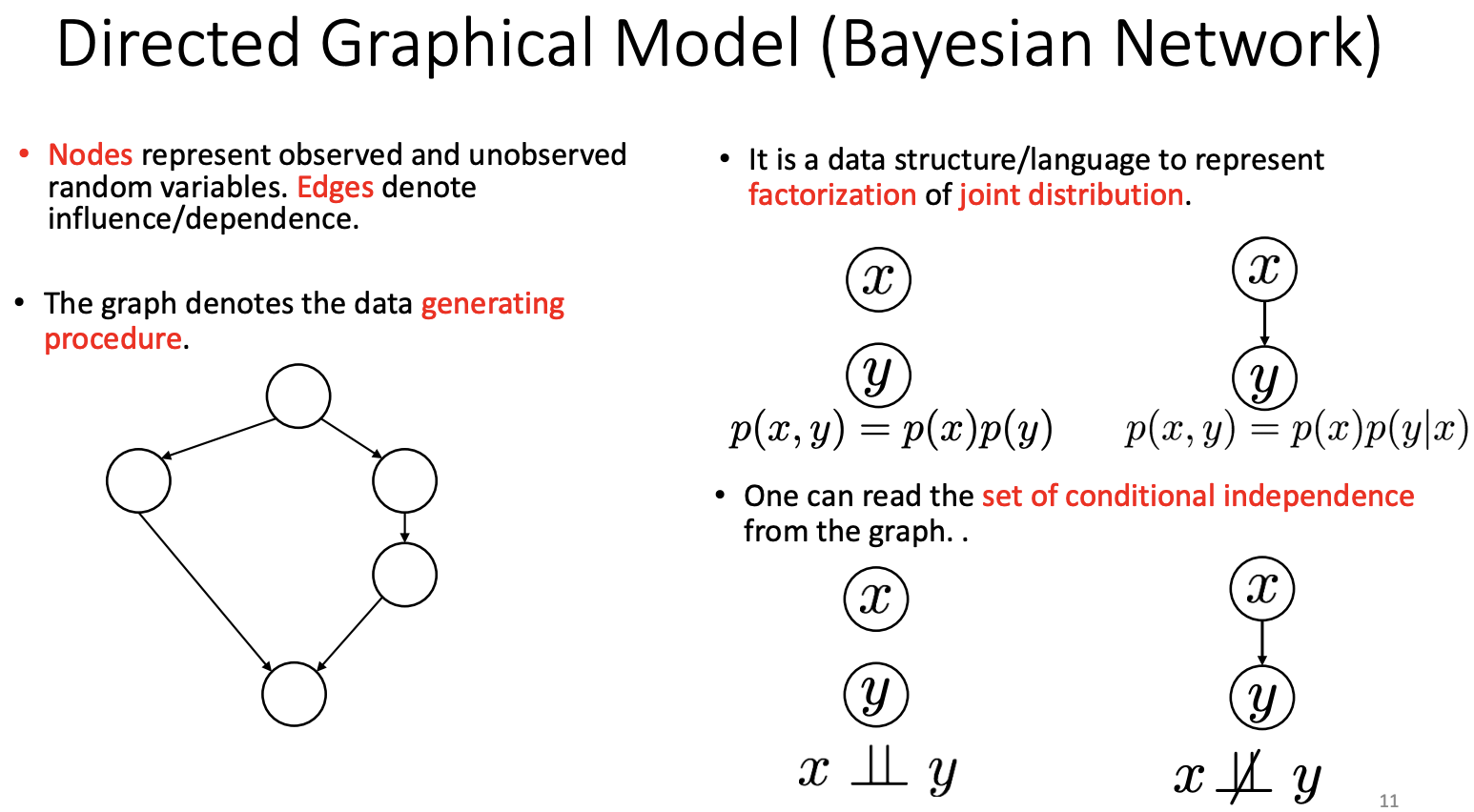
Directed Acyclic Graphical (DAG)

Wrong: I(g) = {A ⊥ C | B} 

A,B,C has 2^N * 2^N * 2^N ($2^(N^3)$) combinations of graph.

I(G) \subset I(P)

G0's I-map: I(G_0) = {X⊥Y}

G1's I-map: I(G_1) = \O

G2's I-map: I(G_2) = \o

https://www.youtube.com/watch?v=yDs_q6jKHb0 

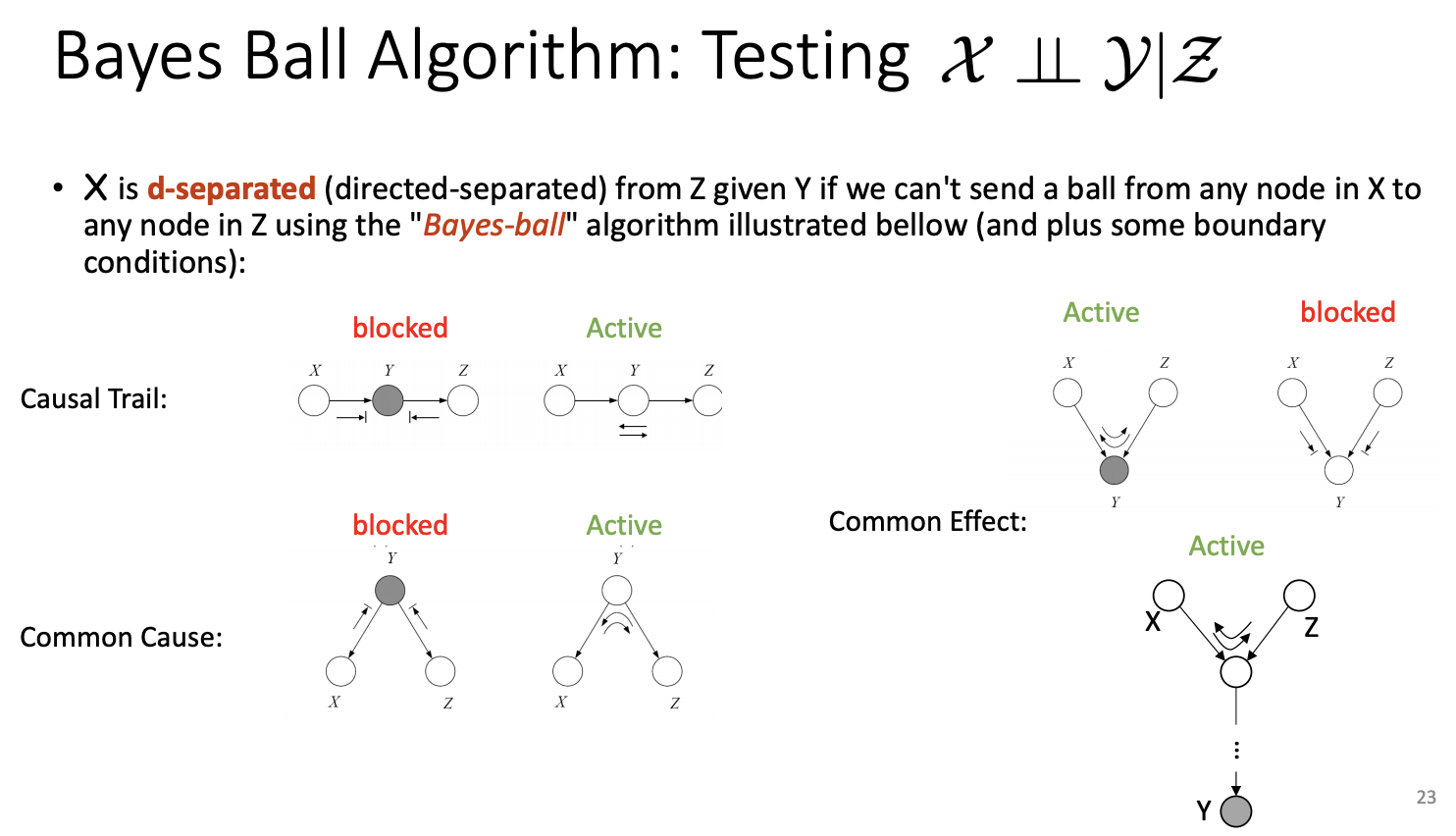
 D-Separation

 

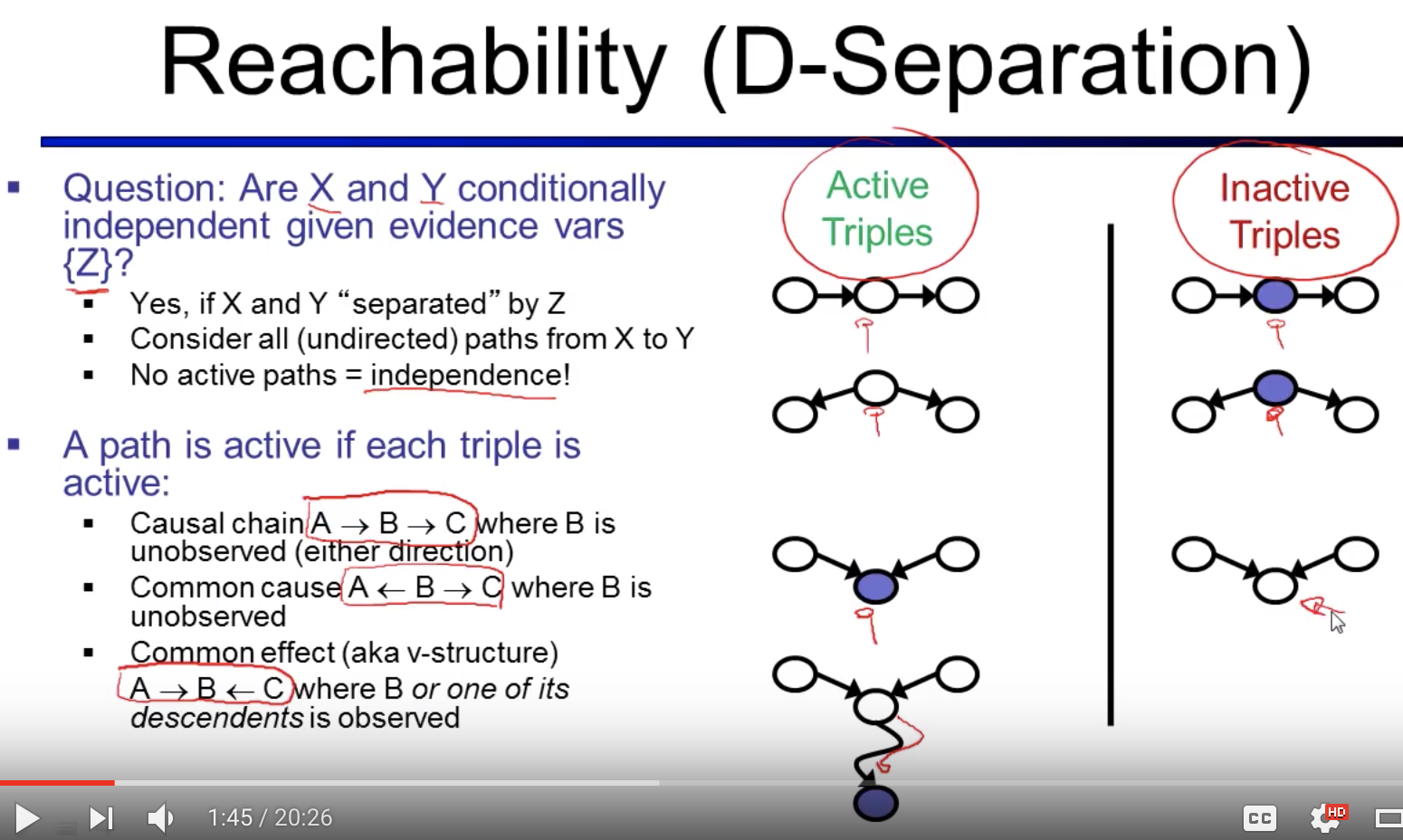
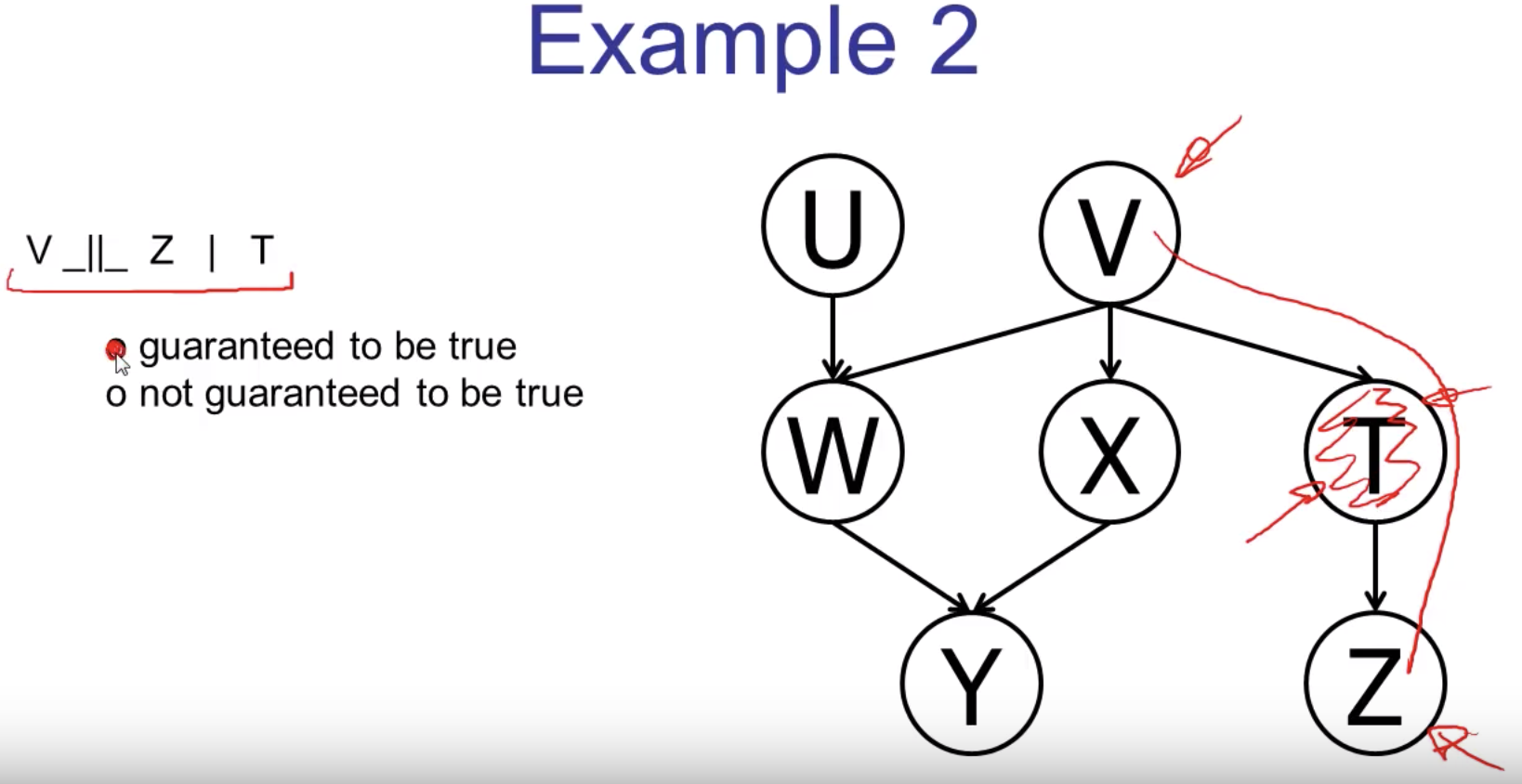
 ... More examples

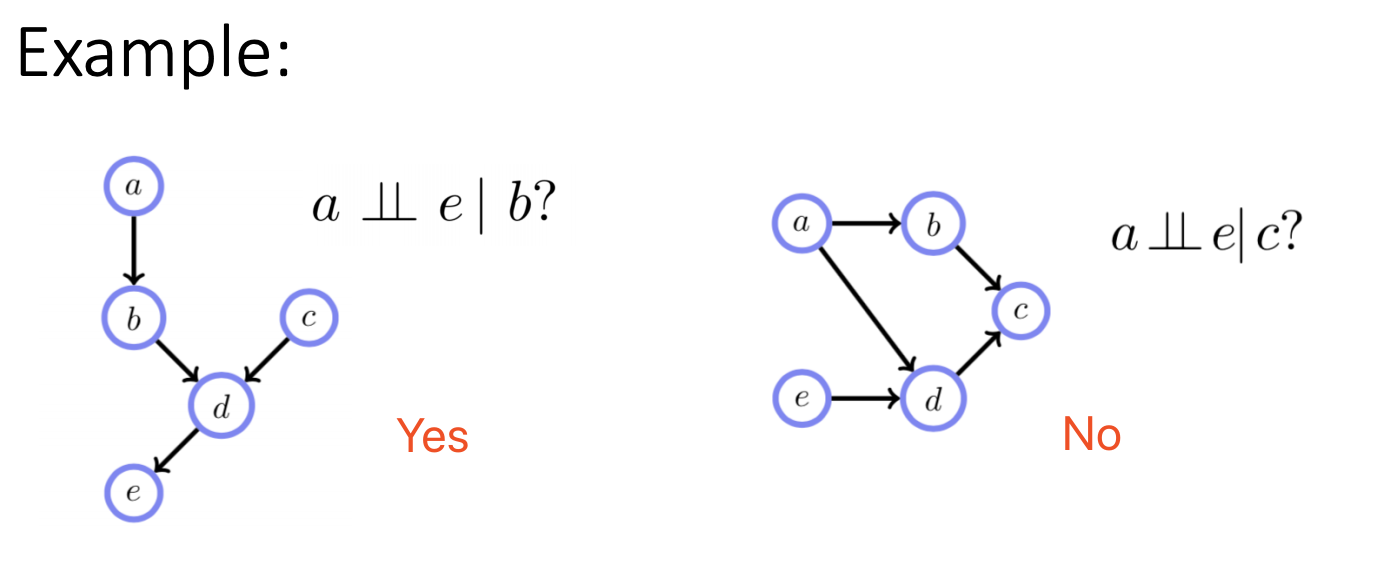
https://stats.stackexchange.com/questions/258012/explanation-of-i-map-in-a-markov-bayesian-network

Explanation of I-map in a Markov/Bayesian network

（a） satisfies

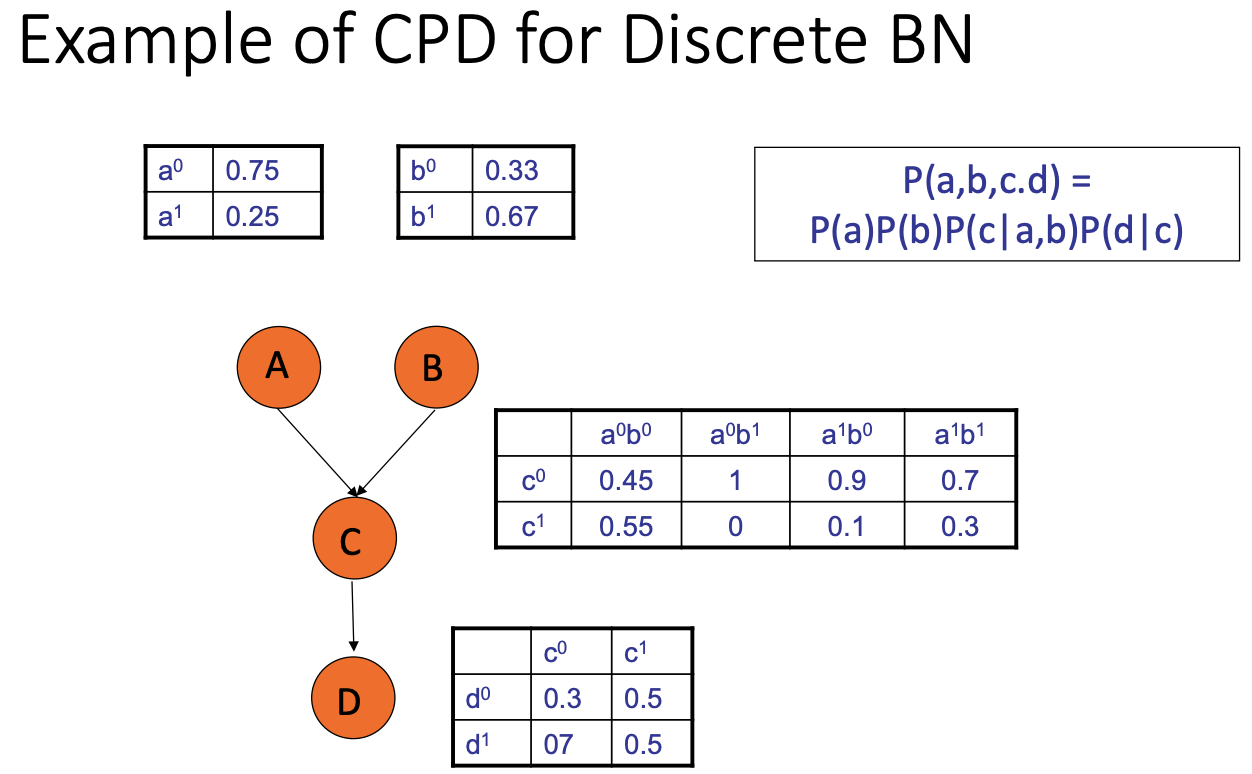
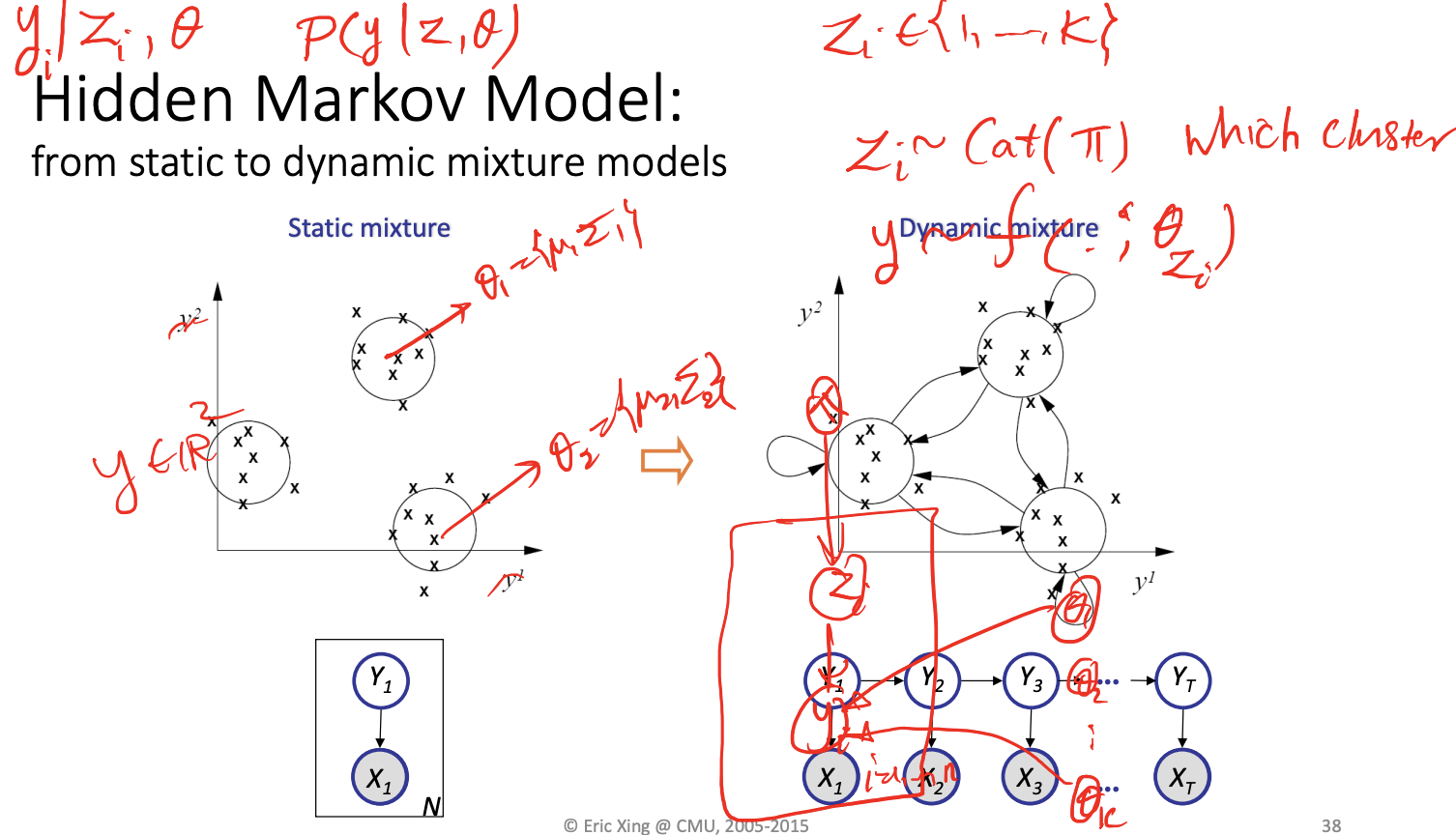
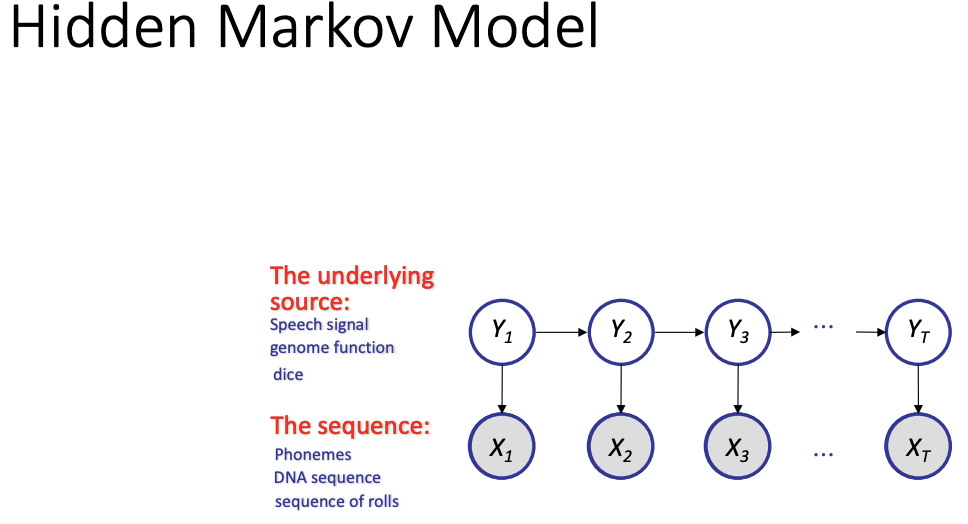
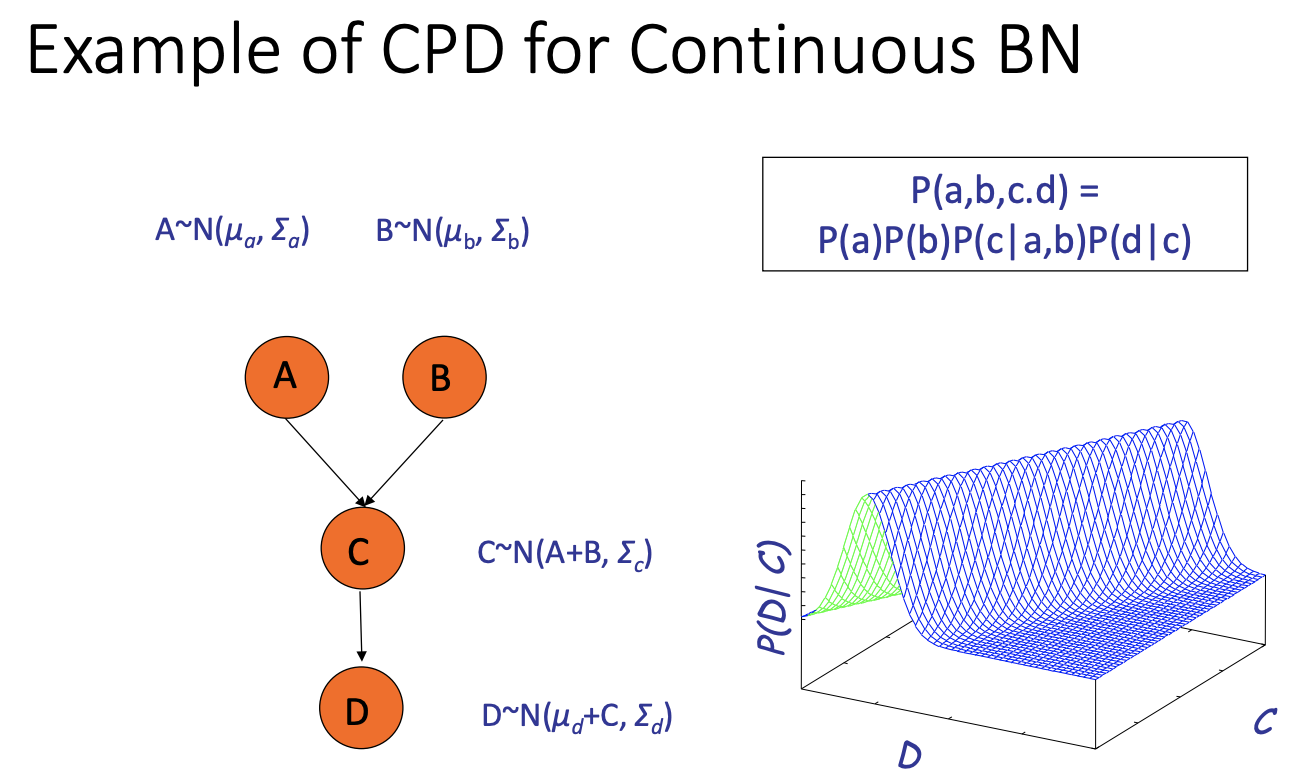
BN: Bayesian Network

CPD: conditional probability distribution 

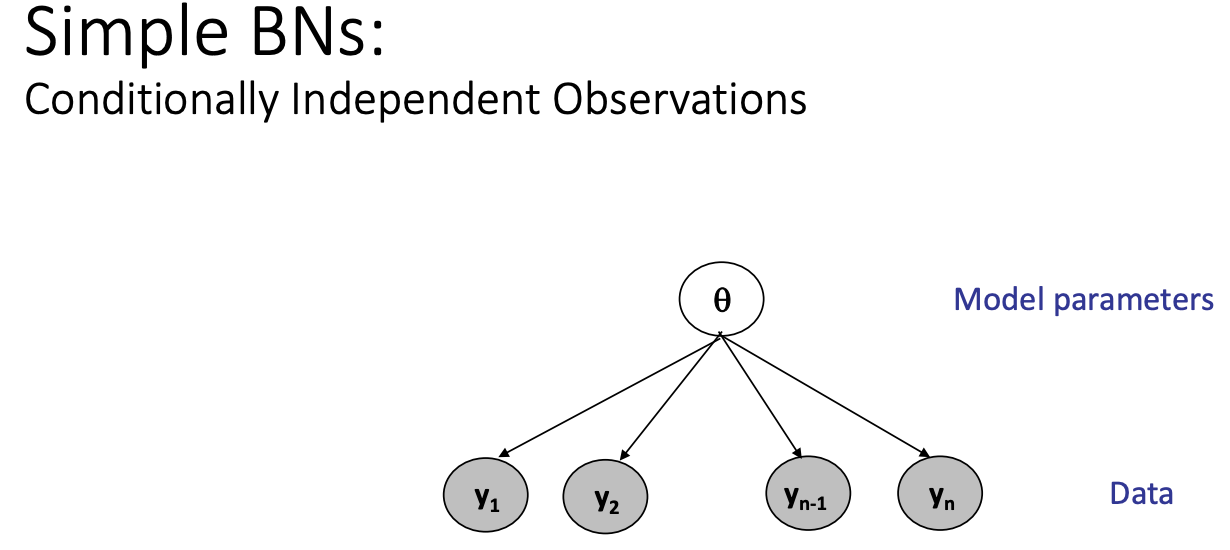
\theta_1 and \theta_k are outside of the box