Not in the frontier of research, but the results are used commonly now.

X_{k+1} - X_n are known,

to calculate the joint probability, we have to do inference

 Recent research: on the approximate inference teches

approx:

1) optimization-based

2) sampling-based

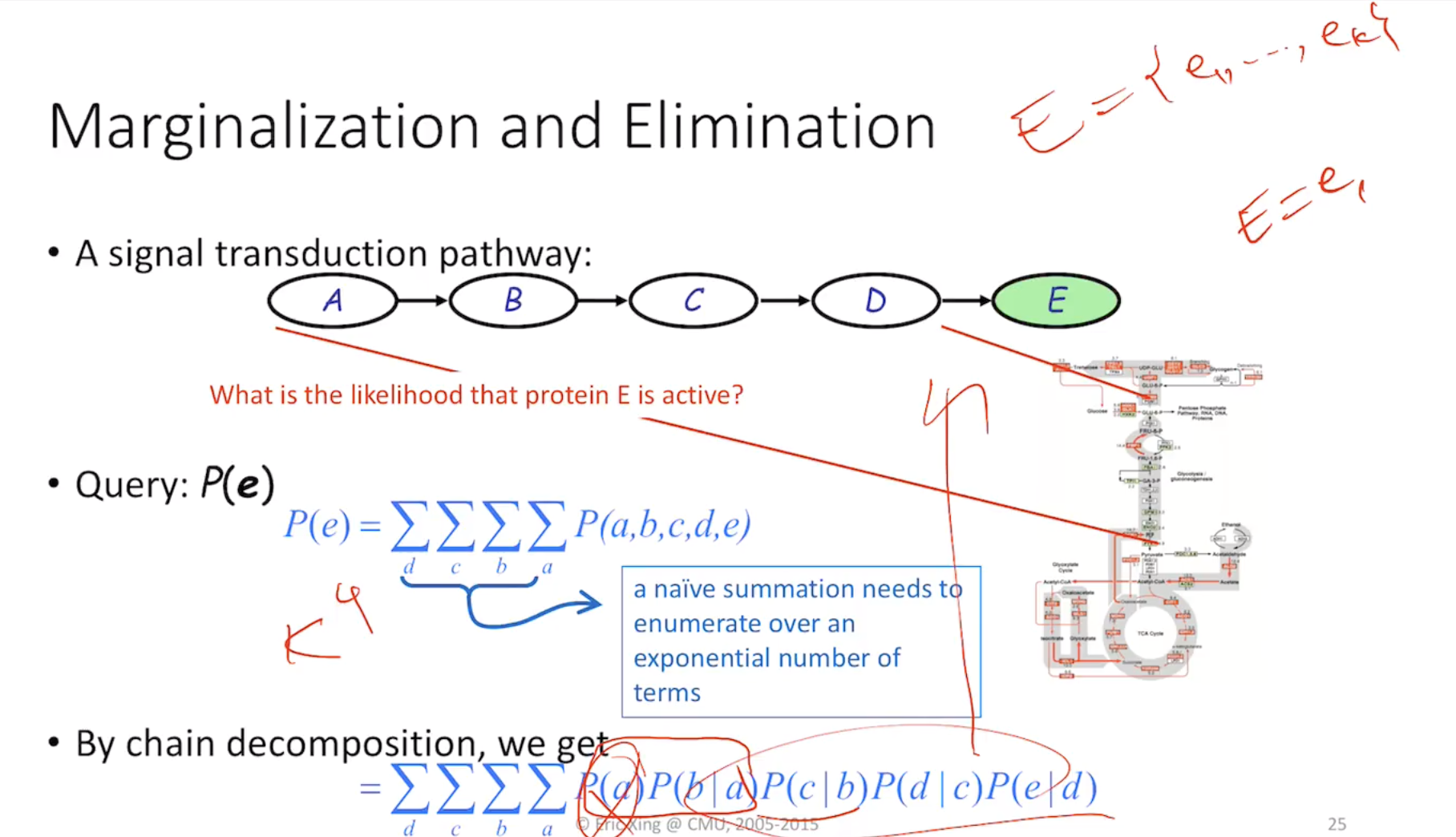
Compare the computational complexity:

    NAIVE way: K^n

    Chain rule:  n*K^2

    n=4

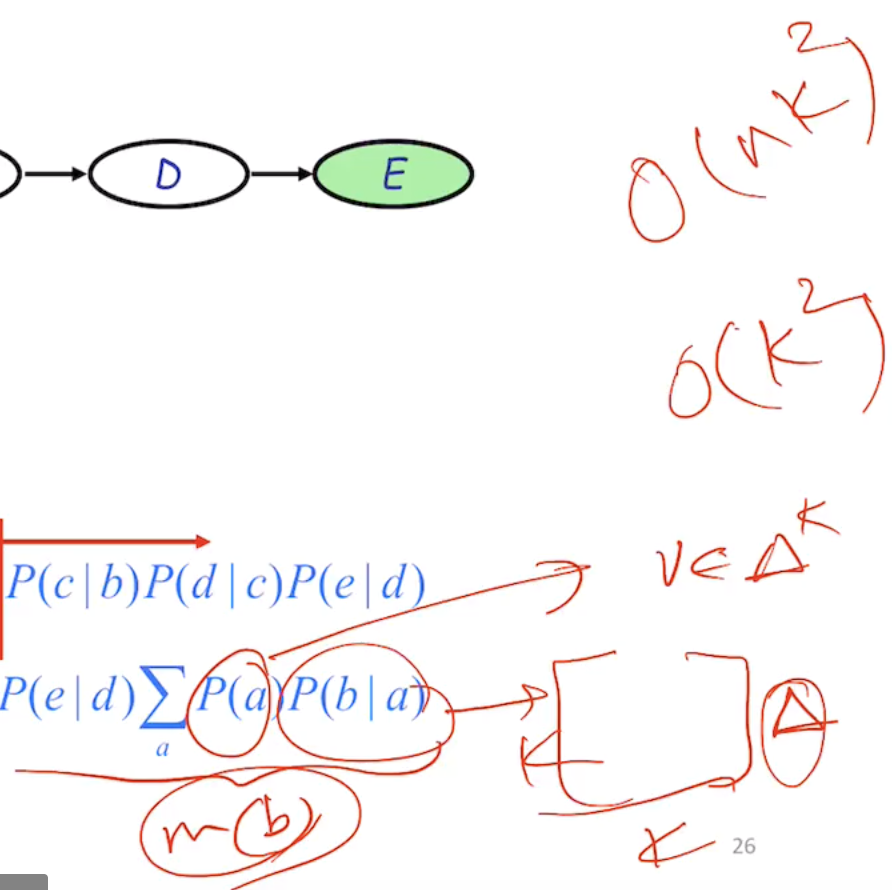
Chain rule derivation:

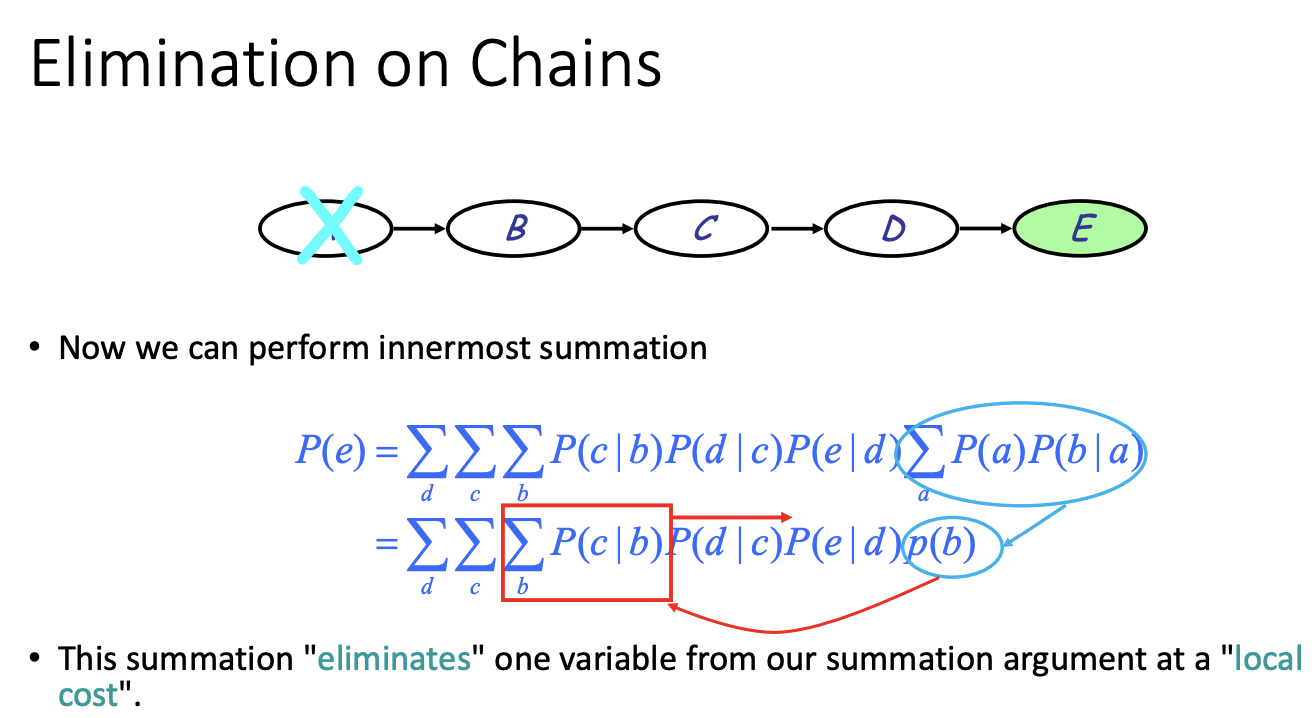
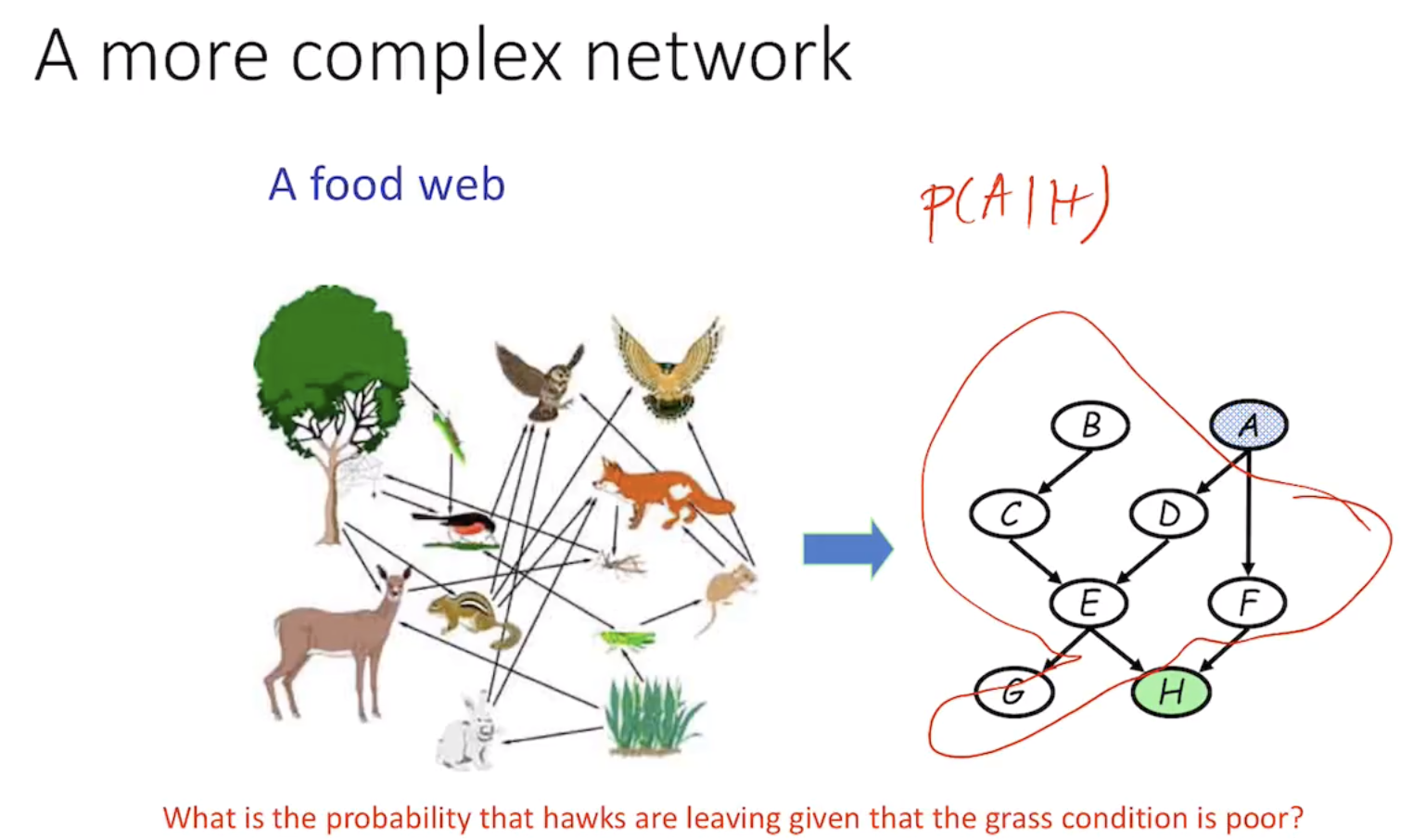
marginalizing out the rest 

 P(a) P(b) P(c|b) ...... P(h|e,f) => a,b,c,d,e,f,g,h (elimation sequence)

introduce a term m_h(e,f) to make e and f dependent

not introducing any dependency here

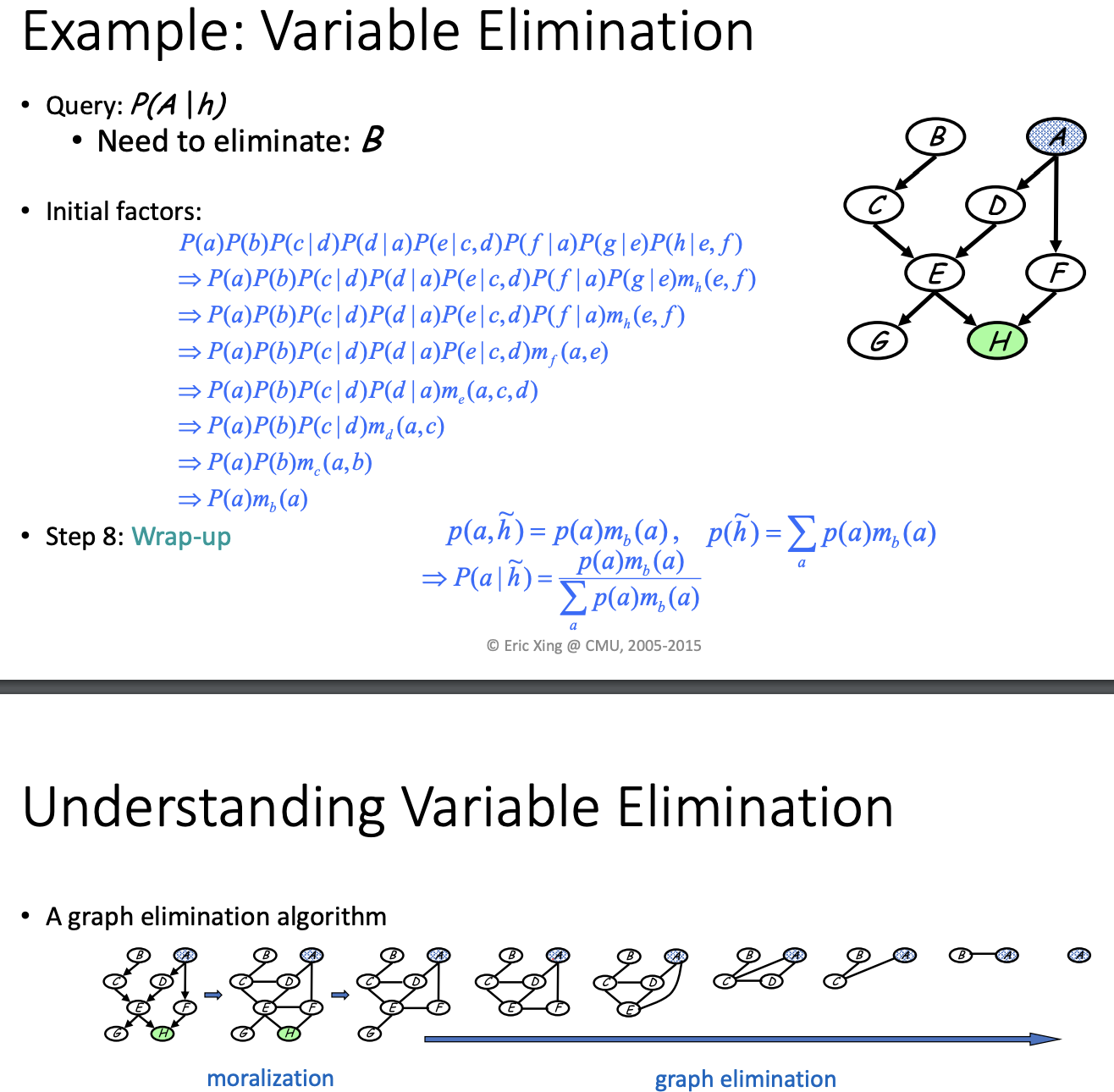
Different elimination sequence will lead to different computational complexity.

It's dependent on how large the new clique is

In one step, if you connect every vertex, then you are in trouble.

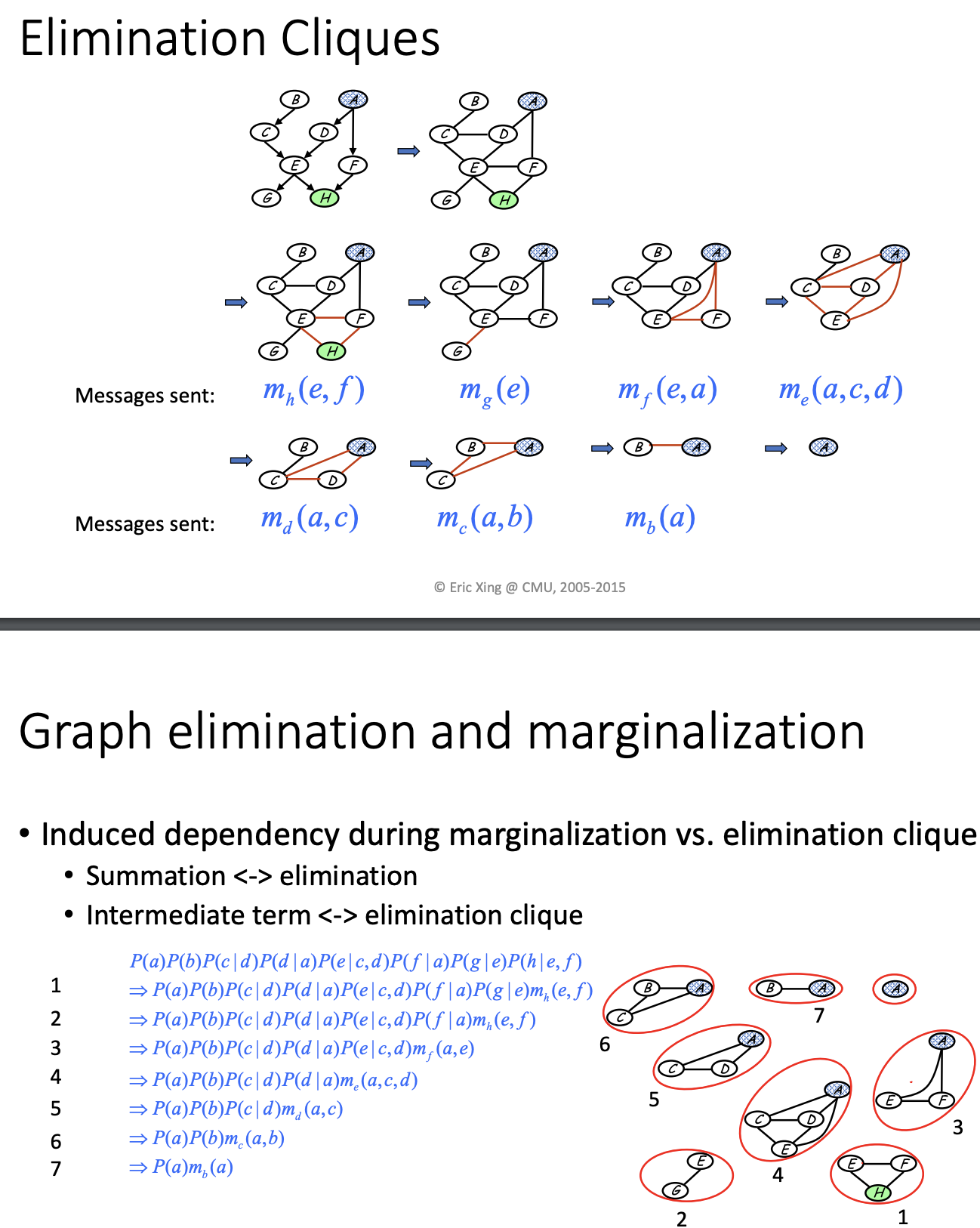
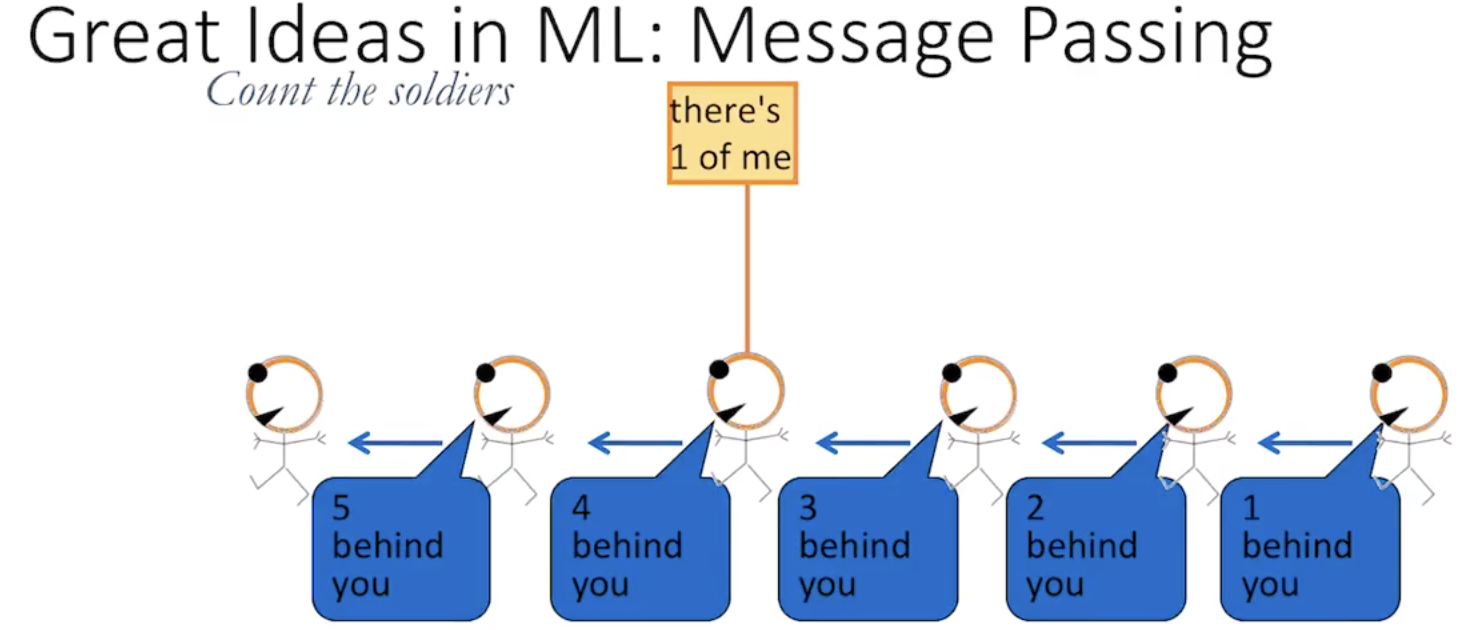
if there's a loop in graph, you can't view message passing as a variable to another variable, but clique to clique.