此處參考《python資料分析和挖掘實戰》這本書

資料質量分析：

主要是對異常值的分析：

1、3σ原則：如果資料符合正態分佈，那麼資料異常定義在一組測定值與平均值的偏差超過3倍標準差的值。在正態分佈的假設下，距離平均值3σ之外的值出現的概率為P(|x-μ|>3σ)≤0.003，屬於極個別的小概率事件。但面對不服從正態分佈的資料，應該怎麼辦呢？

2、箱型圖法：該方法具有很大的魯棒性：多達25%的資料可以離得非常遠而不影響四分位數。異常值被定義為>Q_u+1.5IQR或者<Q_L-1.5IQR。首先將資料從小到大排序，設定位於25%的值Q_L為下四分位數(1/4分位數)，設定位於75%的值Q_u為上四分位數(3/4分位數)，其中IQR稱為四分位間距數，等於Q_u-Q_L，包括了觀察值的一半。

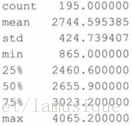
在python中，data.describe()方法可獲得箱型圖法的大部分資料。直接給出樣本資料的一些基本統計量，包括均值、標準差、最大值、最小值、分位數等，如下輸出。

其他資料質量分析還包括對缺失值分析、一致性分析。

資料特徵分析：

分佈分析：極差分組、頻率分佈直方圖(餅狀圖)

統計量分析：平均水平的指標(個體集中趨勢):均值、中位數；變異程度(個體離開平均水平度量):標準差(方差)、四分位間距

週期性分析：週期性規律

貢獻度分析：二八原則—20%的人決定80%的價值

相關性分析：散點圖、計算相關係數

偷點懶直接截圖了。

相對於統計函式則簡單得多，pandas內部含有計算資料樣本的Spearman(pearson)相關係數矩陣的函式corr()，D.corr(method=’pearson’),其中樣本D可為DataFrame，返回相關係數矩陣，method引數為計算方法，支援pearson(default)、kendall、spearman。

還包括D.sum()按列求和、D.std()、D.mean()、D.var()方差、D.cov()其中D均可為DataFrame或Series

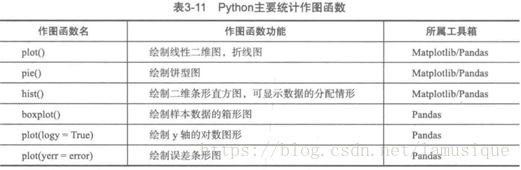
視覺化函式：

主要是matplotlib和pandas函式。

函式plot：需要注意plt.plot(x,y,S)這是matplotlib裡面的，D.plot(kind=’box’)這是pandas裡面的，kind還可以為line(線)、bar(條形)、barh、hist(直方圖)、box(箱線圖)、kde(密度圖)、area、pie(餅圖)。

函式pie：plt.pie(size) 其中size為所佔比例

函式hist：plt.hist(x,y) x為待繪製直方圖的一維陣列，y可以為整數表示均勻分為n組

其他對於pandas呼叫均採用D.xxx()，D可為DataFrame或者Series。