FP-Tree頻繁模式樹演算法
介紹
FP-Tree演算法全稱是FrequentPattern Tree演算法,就是頻繁模式樹演算法,他與Apriori演算法一樣也是用來挖掘頻繁項集的,不過不同的是,FP-Tree演算法是Apriori演算法的優化處理,他解決了Apriori演算法在過程中會產生大量的候選集的問題,而FP-Tree演算法則是發現頻繁模式而不產生候選集。但是頻繁模式挖掘出來後,產生關聯規則的步驟還是和Apriori是一樣的。
演算法原理
FP樹,FP樹,那他當然是最終被構造成一個樹的形狀了。所以步驟如下:
1、建立根節點,用NULL標記。
2、統計所有的事務資料,統計事務中各個型別項的總支援度(在下面的例子中就是各個商品ID的總個數)
3、依次讀取每條事務,比如T1, 1, 2, 5,因為按照總支援度計數數量降序排列,輸入的資料順序就是2, 1, 5,然後掛到根節點上。
4、依次讀取後面的事務,並以同樣的方式加入的FP樹中,順著根節點路徑新增,並更新節點上的支援度計數。
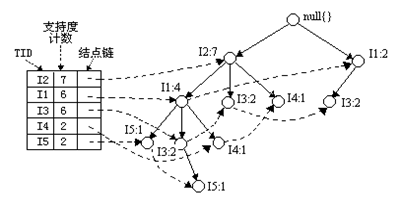
最後就會形成這樣的一棵樹:
然後還要新建一個項頭表,代表所有節點的型別和支援度計數。這個東西在後面會有大用處。如果你以為FP樹的演算法過程到這裡就結束了,你就大錯特錯了,演算法的終結過程為最後的FP樹只包括但路徑,就是樹呈現直線形式,也就是節點都只有1個孩子或沒有孩子,順著一條線下來,沒有其他的分支。這就算是一條挖掘出的頻繁模式。所以上面的演算法還要繼續遞迴的構造FP樹,遞迴構造FP樹的過程:
1、這時我們從最下面的I5開始取出。把I5加入到字尾模式中。字尾模式到時會於頻繁模式組合出現構成最終的頻繁模式。
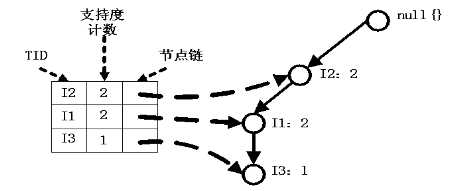
2、獲取頻繁模式基,<I2, Ii>,<I2, I1, I3>,計數為I5節點的count值,然後以這2條件模式基為輸入的事務,繼續構造一個新的FP樹
3、這就是我們要達到的FP樹單路徑的目標了,不過這裡個要求,要把支援度計數不夠的點排除,這裡的I3:1就不符號,所以最後I5字尾模式下的<I2, I1>與I5的組合模式了,就為<I2, I5>, <I1, I5>,<I1, I2, I5>。
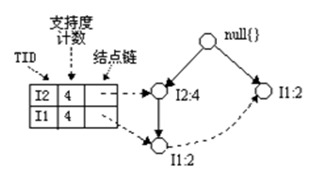
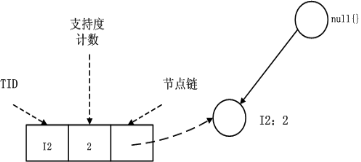
I5下的挖掘頻繁模式是比較簡單的,沒有出現遞迴,看一下I3下的遞迴構造,這就不簡單了,同樣的操作,最後就會出現下面這幅圖的樣子:發現還不是單條路徑,繼續遞迴構造,此時的字尾模式硬臥I3+I1,就是<I3, I1>,然後就來到了下面這幅圖的情形了。
後面的例子會有更詳細的說明。
演算法的實現
輸入資料如下:
|
交易ID |
商品ID列表 |
|
T100 |
I1,I2,I5 |
|
T200 |
I2,I4 |
|
T300 |
I2,I3 |
|
T400 |
I1,I2,I4 |
|
T500 |
I1,I3 |
|
T600 |
I2,I3 |
|
T700 |
I1,I3 |
|
T800 |
I1,I2,I3,I5 |
|
T900 |
I1,I2,I3 |
T1 1 2 5
T2 2 4
T3 2 3
T4 1 2 4
T5 1 3
T6 2 3
T7 1 3
T8 1 2 3 5
T9 1 2 3 /**
* FP樹節點
*
* @author lyq
*
*/
public class TreeNode implements Comparable<TreeNode>, Cloneable{
// 節點類別名稱
private String name;
// 計數數量
private Integer count;
// 父親節點
private TreeNode parentNode;
// 孩子節點,可以為多個
private ArrayList<TreeNode> childNodes;
public TreeNode(String name, int count){
this.name = name;
this.count = count;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getCount() {
return count;
}
public void setCount(Integer count) {
this.count = count;
}
public TreeNode getParentNode() {
return parentNode;
}
public void setParentNode(TreeNode parentNode) {
this.parentNode = parentNode;
}
public ArrayList<TreeNode> getChildNodes() {
return childNodes;
}
public void setChildNodes(ArrayList<TreeNode> childNodes) {
this.childNodes = childNodes;
}
@Override
public int compareTo(TreeNode o) {
// TODO Auto-generated method stub
return o.getCount().compareTo(this.getCount());
}
@Override
protected Object clone() throws CloneNotSupportedException {
// TODO Auto-generated method stub
//因為物件內部有引用,需要採用深拷貝
TreeNode node = (TreeNode)super.clone();
if(this.getParentNode() != null){
node.setParentNode((TreeNode) this.getParentNode().clone());
}
if(this.getChildNodes() != null){
node.setChildNodes((ArrayList<TreeNode>) this.getChildNodes().clone());
}
return node;
}
}
package DataMining_FPTree;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.Map;
/**
* FPTree演算法工具類
*
* @author lyq
*
*/
public class FPTreeTool {
// 輸入資料檔案位置
private String filePath;
// 最小支援度閾值
private int minSupportCount;
// 所有事物ID記錄
private ArrayList<String[]> totalGoodsID;
// 各個ID的統計數目對映表項,計數用於排序使用
private HashMap<String, Integer> itemCountMap;
public FPTreeTool(String filePath, int minSupportCount) {
this.filePath = filePath;
this.minSupportCount = minSupportCount;
readDataFile();
}
/**
* 從檔案中讀取資料
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
String[] temp;
int count = 0;
itemCountMap = new HashMap<>();
totalGoodsID = new ArrayList<>();
for (String[] a : dataArray) {
temp = new String[a.length - 1];
System.arraycopy(a, 1, temp, 0, a.length - 1);
totalGoodsID.add(temp);
for (String s : temp) {
if (!itemCountMap.containsKey(s)) {
count = 1;
} else {
count = ((int) itemCountMap.get(s));
// 支援度計數加1
count++;
}
// 更新表項
itemCountMap.put(s, count);
}
}
}
/**
* 根據事物記錄構造FP樹
*/
private void buildFPTree(ArrayList<String> suffixPattern,
ArrayList<ArrayList<TreeNode>> transctionList) {
// 設定一個空根節點
TreeNode rootNode = new TreeNode(null, 0);
int count = 0;
// 節點是否存在
boolean isExist = false;
ArrayList<TreeNode> childNodes;
ArrayList<TreeNode> pathList;
// 相同型別節點連結串列,用於構造的新的FP樹
HashMap<String, ArrayList<TreeNode>> linkedNode = new HashMap<>();
HashMap<String, Integer> countNode = new HashMap<>();
// 根據事物記錄,一步步構建FP樹
for (ArrayList<TreeNode> array : transctionList) {
TreeNode searchedNode;
pathList = new ArrayList<>();
for (TreeNode node : array) {
pathList.add(node);
nodeCounted(node, countNode);
searchedNode = searchNode(rootNode, pathList);
childNodes = searchedNode.getChildNodes();
if (childNodes == null) {
childNodes = new ArrayList<>();
childNodes.add(node);
searchedNode.setChildNodes(childNodes);
node.setParentNode(searchedNode);
nodeAddToLinkedList(node, linkedNode);
} else {
isExist = false;
for (TreeNode node2 : childNodes) {
// 如果找到名稱相同,則更新支援度計數
if (node.getName().equals(node2.getName())) {
count = node2.getCount() + node.getCount();
node2.setCount(count);
// 標識已找到節點位置
isExist = true;
break;
}
}
if (!isExist) {
// 如果沒有找到,需新增子節點
childNodes.add(node);
node.setParentNode(searchedNode);
nodeAddToLinkedList(node, linkedNode);
}
}
}
}
// 如果FP樹已經是單條路徑,則輸出此時的頻繁模式
if (isSinglePath(rootNode)) {
printFrequentPattern(suffixPattern, rootNode);
System.out.println("-------");
} else {
ArrayList<ArrayList<TreeNode>> tList;
ArrayList<String> sPattern;
if (suffixPattern == null) {
sPattern = new ArrayList<>();
} else {
// 進行一個拷貝,避免互相引用的影響
sPattern = (ArrayList<String>) suffixPattern.clone();
}
// 利用節點連結串列構造新的事務
for (Map.Entry entry : countNode.entrySet()) {
// 新增到字尾模式中
sPattern.add((String) entry.getKey());
//獲取到了條件模式機,作為新的事務
tList = getTransactionList((String) entry.getKey(), linkedNode);
System.out.print("[字尾模式]:{");
for(String s: sPattern){
System.out.print(s + ", ");
}
System.out.print("}, 此時的條件模式基:");
for(ArrayList<TreeNode> tnList: tList){
System.out.print("{");
for(TreeNode n: tnList){
System.out.print(n.getName() + ", ");
}
System.out.print("}, ");
}
System.out.println();
// 遞迴構造FP樹
buildFPTree(sPattern, tList);
// 再次移除此項,構造不同的字尾模式,防止對後面造成干擾
sPattern.remove((String) entry.getKey());
}
}
}
/**
* 將節點加入到同類型節點的連結串列中
*
* @param node
* 待加入節點
* @param linkedList
* 連結串列圖
*/
private void nodeAddToLinkedList(TreeNode node,
HashMap<String, ArrayList<TreeNode>> linkedList) {
String name = node.getName();
ArrayList<TreeNode> list;
if (linkedList.containsKey(name)) {
list = linkedList.get(name);
// 將node新增到此佇列中
list.add(node);
} else {
list = new ArrayList<>();
list.add(node);
linkedList.put(name, list);
}
}
/**
* 根據連結串列構造出新的事務
*
* @param name
* 節點名稱
* @param linkedList
* 連結串列
* @return
*/
private ArrayList<ArrayList<TreeNode>> getTransactionList(String name,
HashMap<String, ArrayList<TreeNode>> linkedList) {
ArrayList<ArrayList<TreeNode>> tList = new ArrayList<>();
ArrayList<TreeNode> targetNode = linkedList.get(name);
ArrayList<TreeNode> singleTansaction;
TreeNode temp;
for (TreeNode node : targetNode) {
singleTansaction = new ArrayList<>();
temp = node;
while (temp.getParentNode().getName() != null) {
temp = temp.getParentNode();
singleTansaction.add(new TreeNode(temp.getName(), 1));
}
// 按照支援度計數得反轉一下
Collections.reverse(singleTansaction);
for (TreeNode node2 : singleTansaction) {
// 支援度計數調成與模式字尾一樣
node2.setCount(node.getCount());
}
if (singleTansaction.size() > 0) {
tList.add(singleTansaction);
}
}
return tList;
}
/**
* 節點計數
*
* @param node
* 待加入節點
* @param nodeCount
* 計數對映圖
*/
private void nodeCounted(TreeNode node, HashMap<String, Integer> nodeCount) {
int count = 0;
String name = node.getName();
if (nodeCount.containsKey(name)) {
count = nodeCount.get(name);
count++;
} else {
count = 1;
}
nodeCount.put(name, count);
}
/**
* 顯示決策樹
*
* @param node
* 待顯示的節點
* @param blankNum
* 行空格符,用於顯示樹型結構
*/
private void showFPTree(TreeNode node, int blankNum) {
System.out.println();
for (int i = 0; i < blankNum; i++) {
System.out.print("\t");
}
System.out.print("--");
System.out.print("--");
if (node.getChildNodes() == null) {
System.out.print("[");
System.out.print("I" + node.getName() + ":" + node.getCount());
System.out.print("]");
} else {
// 遞迴顯示子節點
// System.out.print("【" + node.getName() + "】");
for (TreeNode childNode : node.getChildNodes()) {
showFPTree(childNode, 2 * blankNum);
}
}
}
/**
* 待插入節點的抵達位置節點,從根節點開始向下尋找待插入節點的位置
*
* @param root
* @param list
* @return
*/
private TreeNode searchNode(TreeNode node, ArrayList<TreeNode> list) {
ArrayList<TreeNode> pathList = new ArrayList<>();
TreeNode tempNode = null;
TreeNode firstNode = list.get(0);
boolean isExist = false;
// 重新轉一遍,避免出現同一引用
for (TreeNode node2 : list) {
pathList.add(node2);
}
// 如果沒有孩子節點,則直接返回,在此節點下新增子節點
if (node.getChildNodes() == null) {
return node;
}
for (TreeNode n : node.getChildNodes()) {
if (n.getName().equals(firstNode.getName()) && list.size() == 1) {
tempNode = node;
isExist = true;
break;
} else if (n.getName().equals(firstNode.getName())) {
// 還沒有找到最後的位置,繼續找
pathList.remove(firstNode);
tempNode = searchNode(n, pathList);
return tempNode;
}
}
// 如果沒有找到,則新新增到孩子節點中
if (!isExist) {
tempNode = node;
}
return tempNode;
}
/**
* 判斷目前構造的FP樹是否是單條路徑的
*
* @param rootNode
* 當前FP樹的根節點
* @return
*/
private boolean isSinglePath(TreeNode rootNode) {
// 預設是單條路徑
boolean isSinglePath = true;
ArrayList<TreeNode> childList;
TreeNode node;
node = rootNode;
while (node.getChildNodes() != null) {
childList = node.getChildNodes();
if (childList.size() == 1) {
node = childList.get(0);
} else {
isSinglePath = false;
break;
}
}
return isSinglePath;
}
/**
* 開始構建FP樹
*/
public void startBuildingTree() {
ArrayList<TreeNode> singleTransaction;
ArrayList<ArrayList<TreeNode>> transactionList = new ArrayList<>();
TreeNode tempNode;
int count = 0;
for (String[] idArray : totalGoodsID) {
singleTransaction = new ArrayList<>();
for (String id : idArray) {
count = itemCountMap.get(id);
tempNode = new TreeNode(id, count);
singleTransaction.add(tempNode);
}
// 根據支援度數的多少進行排序
Collections.sort(singleTransaction);
for (TreeNode node : singleTransaction) {
// 支援度計數重新歸為1
node.setCount(1);
}
transactionList.add(singleTransaction);
}
buildFPTree(null, transactionList);
}
/**
* 輸出此單條路徑下的頻繁模式
*
* @param suffixPattern
* 字尾模式
* @param rootNode
* 單條路徑FP樹根節點
*/
private void printFrequentPattern(ArrayList<String> suffixPattern,
TreeNode rootNode) {
ArrayList<String> idArray = new ArrayList<>();
TreeNode temp;
temp = rootNode;
// 用於輸出組合模式
int length = 0;
int num = 0;
int[] binaryArray;
while (temp.getChildNodes() != null) {
temp = temp.getChildNodes().get(0);
// 篩選支援度係數大於最小閾值的值
if (temp.getCount() >= minSupportCount) {
idArray.add(temp.getName());
}
}
length = idArray.size();
num = (int) Math.pow(2, length);
for (int i = 0; i < num; i++) {
binaryArray = new int[length];
numToBinaryArray(binaryArray, i);
// 如果字尾模式只有1個,不能輸出自身
if (suffixPattern.size() == 1 && i == 0) {
continue;
}
System.out.print("頻繁模式:{【字尾模式:");
// 先輸出固有的字尾模式
if (suffixPattern.size() > 1
|| (suffixPattern.size() == 1 && idArray.size() > 0)) {
for (String s : suffixPattern) {
System.out.print(s + ", ");
}
}
System.out.print("】");
// 輸出路徑上的組合模式
for (int j = 0; j < length; j++) {
if (binaryArray[j] == 1) {
System.out.print(idArray.get(j) + ", ");
}
}
System.out.println("}");
}
}
/**
* 數字轉為二進位制形式
*
* @param binaryArray
* 轉化後的二進位制陣列形式
* @param num
* 待轉化數字
*/
private void numToBinaryArray(int[] binaryArray, int num) {
int index = 0;
while (num != 0) {
binaryArray[index] = num % 2;
index++;
num /= 2;
}
}
}
/**
* FPTree頻繁模式樹演算法
* @author lyq
*
*/
public class Client {
public static void main(String[] args){
String filePath = "C:\\Users\\lyq\\Desktop\\icon\\testInput.txt";
//最小支援度閾值
int minSupportCount = 2;
FPTreeTool tool = new FPTreeTool(filePath, minSupportCount);
tool.startBuildingTree();
}
}
[字尾模式]:{3, }, 此時的條件模式基:{2, }, {1, }, {2, 1, },
[字尾模式]:{3, 2, }, 此時的條件模式基:
頻繁模式:{【字尾模式:3, 2, 】}
-------
[字尾模式]:{3, 1, }, 此時的條件模式基:{2, },
頻繁模式:{【字尾模式:3, 1, 】}
頻繁模式:{【字尾模式:3, 1, 】2, }
-------
[字尾模式]:{2, }, 此時的條件模式基:
-------
[字尾模式]:{1, }, 此時的條件模式基:{2, },
頻繁模式:{【字尾模式:1, 】2, }
-------
[字尾模式]:{5, }, 此時的條件模式基:{2, 1, }, {2, 1, 3, },
頻繁模式:{【字尾模式:5, 】2, }
頻繁模式:{【字尾模式:5, 】1, }
頻繁模式:{【字尾模式:5, 】2, 1, }
-------
[字尾模式]:{4, }, 此時的條件模式基:{2, }, {2, 1, },
頻繁模式:{【字尾模式:4, 】2, }
-------演算法編碼時的難點
1、在構造樹的時候要重新構建一棵樹的時候,要不能對原來的樹做更改,在此期間用了老的樹的物件,又造成了重複引用的問題了,於是果斷又new了一個TreeNode,只把原樹的name,和count值拿了過來,父子節點關係完全重新構造。
2、在事務生產樹的過程中,把事務對映到TreeNode陣列中,然後過程就是加Node節點或者更新Node節點的count值,過程簡單許多,也許會讓人很難理解,應該個人感覺這樣比較方便,如果是死板的String[]字串陣列的形式,中間還要與TreeNode各種轉化非常麻煩。
3、在計算條件模式基的時候,我是存在了HashMap<String, ArrayList<TreeNode>>map中,並並沒有搞成連結串列的形式,直接在生成樹的時候就全部統計好。
4、此處演算法用了2處遞迴,一個地方是在新增樹節點的時候,搜尋要在哪個node上做新增的方法,searchNode(TreeNode node, ArrayList<TreeNode> list),還有一個是整個的buildFPTree()演算法,都不是能夠一眼就能看明白的地方。希望大家能夠理解我的用意。
FP-Tree演算法的缺點
儘管FP-Tree演算法在挖掘頻繁模式的過程中相較Apriori演算法裡沒有產生候選集了,比Apriori也快了一個數量級上了,但是整體上FP-Tree演算法的時間,空間消耗開銷上還是挺大的。