相關概念：

二分圖：一個圖被分成兩部分，相同的部分沒有邊

匹配：兩兩不含公共端點的邊的集合M稱為匹配

最大匹配：元素最多的M則稱為最大匹配

完美匹配：最大匹配數M滿足：2*M=V

對於二分圖的最大匹配問題，可以加上一個s，一個t，轉為求最大s-t流

二分圖的最小頂點覆蓋

定義：假如選了一個點就相當於覆蓋了以它為端點的所有邊。最小頂點覆蓋就是選擇最少的點（左右兩邊都可選）來覆蓋所有的邊。

方法：最小頂點覆蓋等於二分圖的最大匹配。

我們用二分圖來構造最小頂點覆蓋。

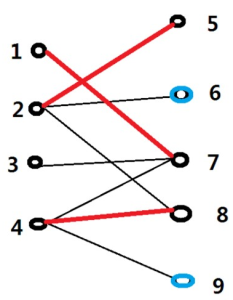
對於上面這個二分圖，頂點分為左右兩個集合，X集合包含1,2,3,4，Y集合包含5,6,7,8,9.假如現在我們已經找到一個最大匹配M，就是上面的紅線所標註的M={(1,7),(2,5),(4,8)}。我們作如下定義：（1）定義1、2、4、5、7、8為已經匹配過的點，其他點為未匹配的點；（2）定義(4,8)、(1,7)、(2,5)為已匹配的邊，其他邊為未匹配的邊。

下面我們從Y集合中找出未匹配的點，就是上面標記的6和9。每次我們從右邊選出一個未匹配的點，從該點出發， 做一條未匹配邊->匹配邊->未匹配邊->……->匹配邊（注意最後以匹配邊結尾），並且標記用到的點，得到下圖：

其中紫色的邊為我們剛才畫的邊，其中標記的點有2、4、5、6、8、9。 上圖的兩條路為：（1）9->4->8->2->5 （2）6->2->5。這兩條路都是未匹配邊->匹配邊->未匹配邊->……->匹配邊。（注意如果一個右側未匹配點有多條邊，那麼這樣的從該點開始的路徑就有多條，上面的6和9都只有一條邊，所以從每個點開始的這樣的路徑只有一條）。

現在我們將左側標記的點2、4和右側未標記的點7選出組成集合S， 那個S就是一個最小頂點覆蓋集，就是S集合可以覆蓋所有的邊。下面證明：

（1）|S|=M，即最小頂點覆蓋等於二分圖最大匹配：左邊標記的點全都為匹配邊的頂點，因為我們構造路徑的時候左邊的點向右找的邊都是最大匹配的邊；右邊未標記的點也為二分圖最大匹配邊的頂點。而且左邊標記的加上有邊未標記的正好是最大匹配的數目。

（2）S能覆蓋所有的邊。所有的邊可以分為下面三種情況：a、左端點標記、右端點標記；這些邊一定被左側標記的點覆蓋，比如上面的2,4；b、右端點未標記；這些邊一定被右側未標記的點覆蓋，比如上面的7；c、左端點未標記、右端點標記。

下面我們證明c這種邊壓根就不會存在：若c是最大匹配中的邊，由於右端點不可能是一條路徑的起點（因為我們的起點都是從Y集合中未匹配的點開始的），於是右端點的標記只能是在構造中從左邊連過來，這是左端點必定被標記了，這時c就轉化成了a；若c屬於未匹配邊，那麼左端點必定是一個匹配點，那麼c的右端點必定是一條路徑的起始點，因此c的左端點也會成為一條路徑的第二個點而被標記，這時c也就成了a。所以c這種邊肯定是不存在的。

（3）S是最小的頂點集：因為最大匹配為M，而|S|=M，所以如果S中的點再少，那麼連M個匹配的邊都不能覆蓋。

二分圖的最大獨立集

定義：選出一些頂點使得這些頂點兩兩不相鄰，則這些點構成的集合稱為獨立集。找出一個包含頂點數最多的獨立集稱為最大獨立集。

方法：最大獨立集=所有頂點數-最小頂點覆蓋

在上面這個圖中最小頂點覆蓋=3，即2,4,7構成最小頂點覆蓋，則其他點6個構成最大獨立集。且其他點不可能相連。假設其他點相連則這條邊必定沒有被2,4,7 覆蓋，與2,4,7是最小頂點覆蓋矛盾。因此其他點之間必定沒有邊。而2,4,7是最小頂點覆蓋，所謂最小就是不能再小了，因此我們的獨立集就是最大了。

二分圖的最大團

定義：對於一般圖來說，團是一個頂點集合，且由該頂點集合誘導的子圖是一個完全圖，簡單說，就是選出一些頂點，這些頂點兩兩之間都有邊。最大團就是使得選出的這個頂點集合最大。對於二分圖來說，我們預設為左邊的所有點之間都有邊，右邊的所有頂點之間都有邊。那麼，實際上，我們是要在左邊找到一個頂點子集X，在右邊找到一個頂點子集Y，使得X中每個頂點和Y中每個頂點之間都有邊。

方法：二分圖的最大團=補圖的最大獨立集。

補圖的定義是：對於二分圖中左邊一點x和右邊一點y，若x和y之間有邊，那麼在補圖中沒有，否則有。

這個方法很好理解，因為最大獨立集是兩兩不相鄰，所以最大獨立集的補圖兩兩相鄰。

二分圖求最大匹配模板：

poj 3041 - Asteroid

思路：

把光束當成頂點，行星當成連線對應光束的邊，這樣轉換後，求的是二分圖最小頂點覆蓋問題，也就是最大匹配問題。

程式碼一：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue> 
 
using namespace std;

struct Edge{
	int from,to,cap,flow;
	Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
const int INF=99999999,maxn=1100;
int n,k,s,t;
vector<Edge> edges;//存正邊和反向邊，邊數的兩倍 
vector<int> G[maxn];//鄰接表，G[i][j]表示節點i的第j條邊在edges陣列中的序號 
int a[maxn];//a[i]表示源點s到節點i的路徑上的最小殘留量 
int p[maxn];//p[i]記錄i的前驅，是用在edges數組裡的序號表示的 

/*void init(int n){
	for(int i=0;i<n;i++){
		G[i].clear();
	}
    edges.clear();
}*/

void AddEdge(int from,int to,int cap){
	edges.push_back(Edge(from,to,cap,0));
	edges.push_back(Edge(to,from,0,0));//反向弧 
	int m=edges.size();
	G[from].push_back(m-2);
	G[to].push_back(m-1);
}

int Maxflow(int s,int t){
	int flow=0;
	for(;;){
		memset(a,0,sizeof(a));
		queue<int> q;
		q.push(s);
		a[s]=INF;
		while(!q.empty()){
			int x=q.front();q.pop();
			
			for(int i=0;i<G[x].size();i++){//x點對應的所有正向弧和反向弧 
				Edge& e=edges[G[x][i]];
				if(!a[e.to]&&e.cap>e.flow){
					p[e.to]=G[x][i];
					a[e.to]=min(a[x],e.cap-e.flow);
					q.push(e.to);
				}
			}
			
			if(a[t])break;
		}
		if(!a[t])break;//如果找不到增廣路，則當前流已經是最大流
		for(int u=t;u!=s;u=edges[p[u]].from){
			edges[p[u]].flow+=a[t];//更新正向流量 
			edges[p[u]^1].flow-=a[t];//更新反向流量 
		} 
		flow+=a[t];//流加上 
	} 
	return flow;
} 

int main(){
	int r,c;
	scanf("%d%d",&n,&k);
	s=0,t=2*n+1;
	for(int i=1;i<=n;i++){
	    AddEdge(s,i,1);	
	}
	for(int i=n+1;i<=2*n;i++){
	    AddEdge(i,t,1);	
	}
	for(int i=0;i<k;i++){
		scanf("%d%d",&r,&c);
		AddEdge(r,n+c,1);
	}
	printf("%d\n",Maxflow(s,t));
}

程式碼二：

利用所有邊的容量都是1以及二分圖的性質，我們還可像下面這樣將二分圖的最大匹配演算法更簡單地實現

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue> 
 
using namespace std;

const int INF=99999999,maxv=1100;
int V;
vector<int> G[maxv];
int match[maxv];
bool used[maxv];
//向圖中增加一條連線u、v的邊 
void add_edge(int u,int v){
	G[u].push_back(v);
	G[v].push_back(u);
}
//dfs找增廣路 
bool dfs(int v){
	used[v]=true;
	for(int i=0;i<G[v].size();i++){
		int u=G[v][i],w=match[u];
		if(w<0||!used[w]&&dfs(w)){
			match[v]=u;
			match[u]=v;
			return true;
		}
	}
	return false;
}
//求解二分圖的最大匹配 
int bipartite_matching(){
	int res=0;
	memset(match,-1,sizeof(match));
	for(int v=0;v<V;v++){
		if(match[v]<0){
			memset(used,0,sizeof(used));
			if(dfs(v)){
				res++;
			}
		}
	}
	return res;
}
int main(){
	int n,k,r,c;
	scanf("%d%d",&n,&k);
	V=n*2;
	for(int i=0;i<k;i++){
		scanf("%d%d",&r,&c);
		add_edge(r-1,n+c-1);
	}
	printf("%d\n",bipartite_matching());
}