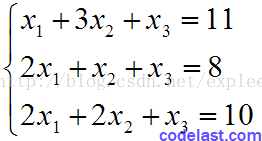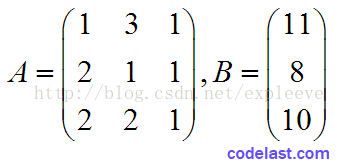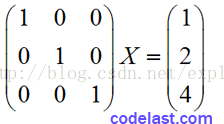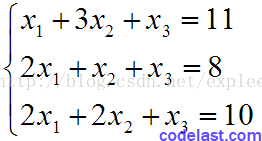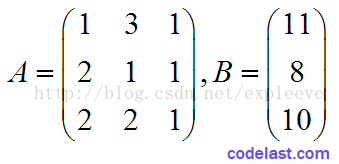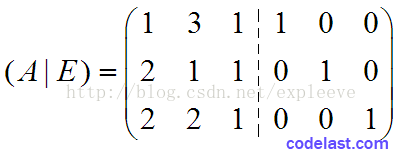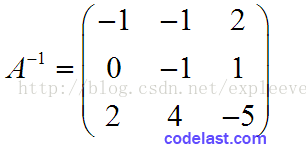高斯-約當消元法（轉）
高斯-約當消元法（轉）
選主元的高斯-約當（Gauss-Jordan）消元法在很多地方都會用到，例如求一個矩陣的逆矩陣、解線性方程組（插一句：LM演算法求解的一個步驟），等等。它的速度不是最快的，但是它非常穩定（來自網上的定義：一個計算方法，如果在使用此方法的計算過程中，舍入誤差得到控制，對計算結果影響較小，稱此方法為數值穩定的），同時它的求解過程也比較清晰明瞭，因而人們使用較多。下面我就用一個例子來告訴你Gauss-Jordan法的求解過程吧。順便再提及一些注意事項以及擴充套件話題。
對本文中所提到的“主元”等概念的解釋，可以參考此連結。
假設有如下的方程組：
寫成矩陣形式就是：AX=B，其中：
且X=(X1, X2, X3)T。
現對矩陣A作初等變換，同時矩陣B也作同樣的初等變換，則當A化為單位矩陣的時候，有：
顯而易見，我們得到了方程組的解X=(1, 2, 4)T。
所以，我們要以一定的策略，對A和B施以一系列的初等變換，當A化為單位矩陣的時候，B就為方程組的解。
選主元的G-J消元法通過這樣的方法來進行初等變換：在每一個迴圈過程中，先尋找到主元，並將主元通過行變換（無需列變換）移動到矩陣的主對角線上，然後將主元所在的行內的所有元素除以主元，使得主元化為1；然後觀察主元所在的列上的其他元素，將它們所在的行減去主元所在的行乘以一定的倍數，使得主元所在的列內、除主元外的其他元素化為0，這樣就使得主元所在的列化為了單位矩陣的形式。這就是一個迴圈內做的工作。然後，在第二輪迴圈的過程中，不考慮上一輪計算過程中主元所在的行和列內的元素，在剩下的矩陣範圍內尋找主元，然後（如果其不在主對角線上的話）將其移動到主對角線上，並再次進行列的處理，將列化為單位矩陣的形式。餘下的步驟依此類推。具體的計算過程的一個例子，請看下面我舉的求逆矩陣的過程。
如果要解係數矩陣相同、右端向量不同的N個方程組，在設計程式的時候，沒有必要”解N次方程組“，我們完全可以在程式中，將所有的右端向量以矩陣的資料結構（類似於二維陣列）來表示，在係數矩陣作行變換的時候，矩陣裡的每一個右端向量也做同樣的變換，這樣，我們在一次求解運算的過程中，實際上就是同時在解N個方程組了，這是要注意的地方。
那麼，G-J法為什麼可以用來求逆矩陣？
假設AX=E，其中，A為n階係數矩陣（與上面的解線性方程組對照）；E為單位矩陣，即E=(e1,e2,…,en)，其中ei (i=1,2,…,n) 為單位列向量；X為n個列向量構成的矩陣，即X=(x1
求逆矩陣時，係數矩陣A和單位矩陣E可以共用一塊儲存區，在每一次約化過程中，係數矩陣逐漸被其逆矩陣替代。
在這裡，我用一個實際的例子來說明G-J法求逆矩陣的過程：
有如下的方程組：
顯而易見，該方程組對應的係數矩陣A和右端向量矩陣B（此處只有一個右端向量）分別為：
其實在求逆矩陣的過程中，矩陣B無關緊要，可以忽略，不過此處還是把它寫出來了。下面，把單位矩陣E附在A的右邊，構成另一個矩陣（A|E）：
下面，我們就通過矩陣的初等變換，將A化為單位矩陣E，而E則化為了A的逆矩陣。以下是轉化步驟：
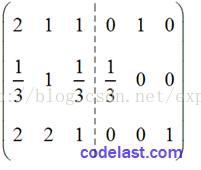
- 【Step 01】主元選為3，所以將Row1（第一行）與Row2（第二行）交換：
- 【Step 02】主元所在行的所有元素除以主元：
- 【Step 03】Row1 - Row2，Row3 - 2 × Row2：
現在，原來的矩陣A有一列被化為了單位陣的形式。
- 【Step 04】重新選主元，這一次主元選為5/3，於是Row1 ÷ 5/3（主元所在行的所有元素除以主元）：
- 【Step 05】Row2 - (1/3) × Row1，Row3 - (4/3) × Row1：
現在，原來的矩陣A又有一列被化為了單位陣的形式。
- 【Step 06】重新選主元，這一次主元選為-1/5，於是Row3 ÷ (-1/5)（主元所在行的所有元素除以主元）：
- 【Step 07】Row1 - (2/5) × Row3，Row2 - (1/5) × Row3：
現在，原來的矩陣A的所有列都被化為了單位陣的形式。
可見，以上過程非常適合於計算機程式設計求解。
至此，我們完成了從A到E的轉換，這個過程中使用了選主元的方法，但沒有使用列交換。於是，原來的單位矩陣E就變成了A-1，即：
有人說，在進行轉化的過程中，如果某一步發現選中的主元為0，怎麼辦？當然，這種情況就進行不下去了（矩陣是奇異的）。