Algorithms, Princeton, Coursera課程整理與回顧
Princeton的演算法課是目前為止我上過的最酣暢淋漓的一門課,得師如此夫復何求,在自己的記憶徹底模糊前,願對這其中一些印象深刻的點做一次完整的整理和回顧,以表敬意。
-
注:
這是一篇更關注個人努力與完成任務專案過程相關的文章,內容集中於課程背後值得提到的部分,不會介紹課程基本資訊及學習時必讀的設定要求等部分,敬請諒解。
在學習一門課程的時候考慮為什麼這麼教是個人習慣,我會嘗試給出一些解讀,為什麼這門課這麼屌(awesome)。
優化無止境,越學習才能越深刻地感受自己的無知,即使是作業內已提到的額外內容我也並沒有一一探究完整,這裡只是謙卑地盡力記錄自己的努力,並無意與誰比較,如有新的進展還會回來更新。
除特別標註外,文章非原創插圖全部來自課程相關資源。
每一小節的作業題目連結到specification,“√”連結到checklist,“〇”連結到code下載。
這裡提供一個全文完整的資源樹。
劇透預警:
內容包含大作業的關鍵問題解法分析。
-
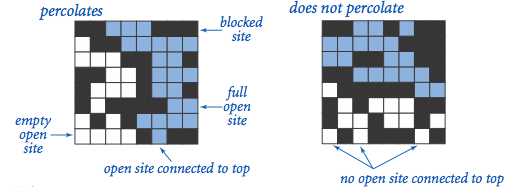
作為第一部分開學第一課,作業Percolation可謂精妙:
1. 既沒有複雜的語法使用(僅陣列操作),又著實比在基礎語言層面上升了一個檔次;
2. 漂亮的visualizer動畫效果激勵著初學者完成任務;
3. 強大的autograder功能初次展現,評價演算法的主要管道一目瞭然,每一微秒每一位元組都很重要;
4. 針對學習迅速的同學還隱含了一個很大的挑戰:在僅使用一個WeightedQuickUnionUF物件的前提下,解決backwash問題。
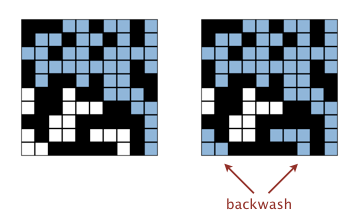
下面主要聊聊backwash:
問題的核心源自virtual top/bottom,一個強行被導師在課程視訊中提到的優化方法,於是天真的同學們(我)就去開心地實現這個看似無辜而又效能楚楚動人的方法,卻毫不瞭解導師在下一節中馬上提出的backwash問題是何物,還覺得這種低階錯誤怎麼可能會發生:
java-algs4 PercolationVisualizer percolation/input10.txt
……
(我發誓這就是我看到的東西……)
把痛碎的心小心拼回,認真思索一番後確定問題根源出在virtual bottom,一個顯而易見的解決方案便浮現在眼前:使用兩個UF,一個使用vb一個不用,判斷percolate用前者,判斷full用後者,解決!
然而checklist的一句話又引起了我的注意:Raw Score 100.00 / 100.00
加上autograder特別溫馨的提醒“bonus failed”,我不得不重新開始審視這個問題。However, many students consider this to be the most challenging and creative part of the assignment (especially if you limit yourself to one union-find object).
後來的事實證明,直到課程結束沒有一個問題再讓我如此頭疼。經過了一段可謂長征式的思考,加之在forum的討論中得到了一點靈感(多加利用Find()),最終形成並實現瞭解決方案,方案核心如下(corner case另行處理):
1. 將原方案中表示open狀態的boolean陣列改為byte陣列,設定規則如下:初始化的預設值0代表blocked site,賦1代表open site,賦2代表與尾行相連的open site;
2. 每open一個site,如果位於尾行則賦2,否則賦1;
3. 分別對每個鄰接site檢測:如任何一方的root site對應byte值為2,將雙方Union後的root site設為2。(root為Find()的返回值)
此方案下,判斷open只需要對應byte>0,判斷full使用UF結果準確,判斷percolates檢測virtual top的root site對應byte是否為2。
Raw Score 101.25 / 100.00
Test 2 (bonus): Check that total memory <= 11 N^2 + 128 N + 1024 bytes
==> passed
對這個作業來說,上面這三行的成績凝聚了太多。
-
第二週課程正式展開,但在作業深度上相對稍有下降,根據指定的效能和API要求,選擇適當的實現方式(動態陣列、單、雙向連結串列),實現Randomized Queue和Deque,主要訓練基本的演算法分析和程式設計嚴謹性(完善處理corner-case),但並無特別的難點。有兩個小技巧可以提出:連結串列可使用sentinel node(s)使程式碼更簡潔(checklist已提),寫client時可先shuffle再插入(bonus)。
過程中一併學習了Java的Generics,Iterable,Iterator概念,在大學課程部分已學習掌握得比較熟練,可不談,the result speaks:
Raw Score 100.19 / 100.00
Test 3 (bonus): Check that maximum size of any or Deque or RandomizedQueue object created is <= k
==> passed
結合兩次作業特性,可看出一些值得一提的點:
作業任務要求與說明往往面面俱到細緻入微,在給定公有API框架及其對應時間空間複雜度的基礎上,結合課程視訊知識內容,這種“受指導”的程式設計過程變得十分清晰,尤其是其中API的設計,風格簡潔高效到自成一家,我認可自己的程式碼風格已很簡潔,而algs4.jar讓我第一次看到了更高;
給定充足的測試材料,包括各類corner-case或相對有趣的輸入資料(如sedgewick60.txt),及合適情況下生動的視覺化工具(如PercolationVisualizer.java),都使得學生可以全力,高效,有動力地,將精力集中在核心演算法本身上。
-
本週的課程介紹了兩大經典排序:Mergesort和Quicksort,自然作業也與sorting緊密相關。Collinear Points(找出所有4個或以上共線的點構成的點集)是第一個在執行時見證“好的演算法”與“暴力演算法”直觀差別的作業,這樣的對比能給學生帶來深刻的影響:忙了好久,為了什麼?
左圖為暴力演算法(~N^4)求解100個數據點(input100.txt),右圖為基於排序的演算法(~N^2logN)求解1423個數據點(rs1423.txt)
測試資料還有很多。圖中示例對快速演算法給定資料量龐大了不止10倍,執行時間卻與不到1/10資料量下的暴力演算法接近;對左圖資料,快速演算法基本看不到找線的動畫過程就完成了;對右圖資料,暴力演算法在可以忍受的時間裡基本找不到幾條線。
這樣的執行結果可以給學生一種非常好的對自己努力的掌控感,正是這樣一個個美妙的瞬間使學生能以最好的狀態與飽滿的好奇心在演算法之路上繼續走下去。
作業說明中對核心演算法的描述非常清晰,應當特別小心的技術點(浮點誤差、正負零等等)也都在checklist中予以強調,因而實現難度不算很大,其中使用了Java的Comparable與Comparator,排序過程呼叫Arrays.sort(),詳細思考問題理清關係後,實現非常自然,前提是程式設計基本功必須紮實。
值得提到的點:
最終實現版本拿到了100分,未發現關於bonus的討論。checklist鼓勵初學者開始編寫快速演算法時先不要擔心5個或以上的點共線的情況,而實際上對基本功紮實的同學,從開始便考慮這個問題更為合適;
checklist提到compare()和FastCollinearPoints類可以完全避免浮點數用整形運算實現,我想到的唯一符合要求(Point.java註釋中規定不得依賴toString())的方法是,對Point類的compareTo()方法返回值增加意義(不單純返回正負1),以獲取兩點的座標之差(因題目給定座標取值範圍0-32767,可在返回值低兩位位元組儲存x座標差, 高兩位位元組儲存y座標差),再利用座標差判斷斜率是否相等。雖依然完全符合題目要求,但已有一點奇技淫巧之嫌,並且不一定能夠通過autograder(評分時會替換Point類去測試FastCollinearPoints),不多討論。(更新:此方法已確定違反FastCollinearPoints的API。)
-
IV. Priority Queue與8 Puzzle √ 〇
剛剛講解完使用Binary Heap實現的Priority Queue,便迎來了這周的8 Puzzle——使用PQ實現A*解決NP難問題,所以——重點在優化咯。
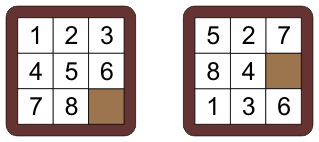
左邊是目標狀態,右邊是起始狀態;對,就是那個——小時候功能手機上的蒙娜麗莎。
隨著學習的深入,這次作業的複雜度有了一個明顯的上升,但這門課最美妙的地方之一也就在這裡:面臨的問題越來越複雜,而導師給出的指導思路依然保持最大程度的簡潔優雅,每一步驟的設定都直指問題核心,並在實現功能基礎上提供非常豐富的優化選擇,以及每個優化會帶來的影響分析。
"It's a funny feeling being took under the wings of a dragon. It's warmer than you think." —— Gangs of New York
整個問題相對比較複雜,但經過給定API的劃分和給定的限制後,問題變成了實現一個個目標明確的小方法而已,其中最複雜的不過是A*的實現,而周到合理的封裝和PQ的使用也使得這個過程無比自然,在此之前我從未意識到我可以將A*在如此短小清晰的程式碼中實現:(原始碼如此,僅省略了宣告過程)
while (!pq.min().board.isGoal()) {
cur = pq.delMin();
for (Board nb : cur.board.neighbors()) {
if (cur.prev != null && nb.equals(cur.prev.board)) continue;
pq.insert(new Node(nb, cur.moves+1, cur));
}
}解決8 Puzzle這一NP難問題的核心程式碼便完成了。
當然,在其餘部分還是有不少值得提到的點:
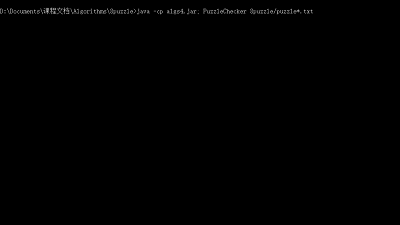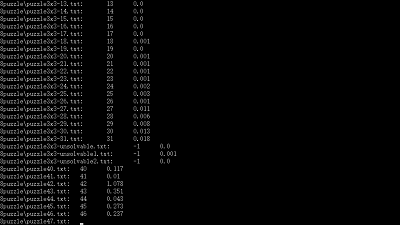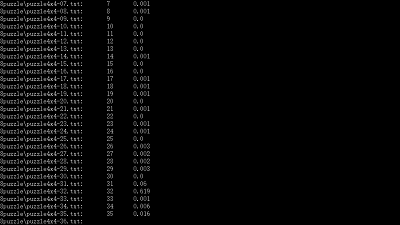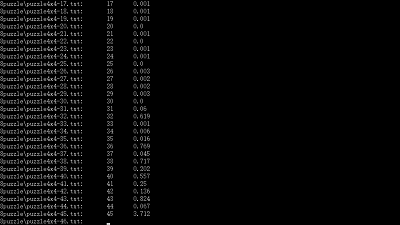
我的最終測試檔案及結果在這裡,運行於i5-2450 (8G),結尾幾個複雜的4x4開始因記憶體不足報錯,論壇查到大概需要5-6G超出了我的空閒記憶體,即使要測也會用到虛擬記憶體,因而結果參考意義不大。用char[]儲存一個Board的狀態比用int[][]好太多,但使用前需要詳細測試將char做數字使用與直接用int的區別;
Board的equals()方法只需比較char[]構成的String即可,早期因圖省事直接比較了toString()的返回值(one-liner),造成了很大的效能損失,最後尋找問題來源也費了不少功夫(教訓:看似再簡單的部分也要在腦袋裡多轉一轉再下手,devil in the details,…,you name it);
Solvability: 這篇文章描述的解決方案應為checklist所述方案,但需要脆弱地依賴toString()反推Board內容,在本期課程的API設定中已被明確禁止,要求使用兩個同步A*的方案解決(最好使用一個PQ),但未來session可能會在兩方案對應API設定間切換,所以我都實現了一遍,上面出現的A*程式碼來自文章所述方案;
實現Priority的cache時需要稍多做思考,直覺想到的第一方案是儲存在Node中與A*過程配合,而這將使A*程式碼迅速腫脹,且沒有很好地利用更多規律:如checklist所指出,對相鄰Board每次重新計算Priority其實也有很多重複工作,我的做法是將cache過程作為Board類一個私有建構函式,構造相鄰Priority只需做對應增量操作即可,以最簡潔的手段達到了目的。
對於這個作業,努力的最終彙報便是,看著終端中puzzle一個個被正確解決沾沾自喜,然後到相關的拓展材料中去體驗無知,發現更大的世界。
-
這一週的Balanced Search Trees課程令我印象深刻。在進入作業討論前,我希望先聊聊這次的課程內容:
在前一週的課程中就已引入了二叉樹的概念,一個無比經典的資料結構,這我在大學課程中便已瞭解到,只是認識非常淺薄,並從未,也從未認為我能夠,動手實現過。
可如果說在上一週的學習中彌補了我的這個問題,對二叉樹有了更深刻的理解,那麼這一週的課程徹底顛覆了曾經心中幼稚的見解,所謂質變,我應該是在這裡體會到的:
從小學四年級開始在少年宮學習BASIC到初中的PASCAL,以致雖然後來停止學習,但因為接觸時間遠早於同齡人而在此方面經歷了各種優勢,但從小在我心中“程式”,以及它背後所代表的機械邏輯始終被認為是“就那麼回事兒”的。我天真地認為自己早已掌握“程式”界的終極真理,無非就是嚴絲合縫一步不差地執行、再執行,只要“機械”性地認真下去,便沒有什麼解決不了的,以至於從小就在性格中造就了一面“徹頭徹尾的唯物+實用主義者”,不相信任何世間美好。
有這句天真的話在前,接著慢慢成長,讀書,行路,閱人,歷事,自然會學到原來這個世界真的不是那樣,開始理解愛與人性,開始理解這個世界的美妙。加上比較幸運,因而“唯心+浪漫主義者”的一面在我的性格里也發展得很好。但大學開始繼續學習計算機,多少,對“程式”這一徹頭徹尾“唯物+實用”精神的產物,還是抱著一些看法的。
結束這一週的課程學習後,我改變了這個看法。
課程開始先講解了2-3 search trees,一種引入了新規則樹型結構。這是一個“理解容易,實現複雜”的Symbol table方案,它可以對任何輸入資料保證樹形結構的平衡以達到保證各項操作logN的複雜度,而規則卻足夠簡單到可以在課堂中很快描述清楚,可以算是課程中第一個令我驚豔的演算法。
這時我想:果然在一步步深入後演算法變得高深莫測了起來呢,這個2-3 tree,理解起來容易,要實現起來可真是困難吶。已經不是二叉樹那麼簡單的東西了,以後是不是隻會更難啊,看來我遇到了一個屏障,這是不是我能走到的最遠了啊。(開始有一點點擔心)
直到視訊結尾出現關於implementation的討論:“Bottom Line: Could do it, but there's a better way.”
緊接著下一節就是我們的主角:左傾紅黑二叉樹(LLRB)。
它只做到了一件事:將2-3 tree帶回了二叉樹世界,卻僅對樸素的二叉樹做極其微小的改動——每個節點增加1 bit,用以表示“顏色”,加之無比簡潔的引導,便在現實世界中實現了原先只是構想的2-3 tree幾乎全部的優點。
紅黑樹本身就是70年代Sedgewick教授參與提出的,而LLRB是由他一手提出的極其簡潔的紅黑樹實現版本,尤其是它的insertion,在課堂上作為重點講解,僅在原樸素二叉樹實現程式碼基礎上,增加了3個小工具函式(左旋、右旋、翻轉)和遞迴插入過程中的4行程式碼(如圖),便完成了所有工作。
在徹底理解LLRB後,我想我被征服了。程式不再僅僅是徹頭徹尾“唯物+實用”精神的產物,而是我們理解世界的工具,也見證著我們改變世界過程,它與其他一切事物一樣,可以充滿真正的美。
我想可以這樣評價紅黑樹背後的思想:這樣的成果也不是憑空出現的:它就像人類從矇昧時代開啟智慧的一道光,將原來鬆散無序的組織變得優雅而高效,並且還尊重了所有舊時代的傳統;
也正是因為尊重傳統,才使得新的秩序得以穩定存在;
新的秩序完整了傳統,成為了傳統當中,最為亮麗的部分。
勇於跳出傳統的框框,用自由的視角審度;(2-3 tree已不是二叉樹)
回到現實在一點一滴中細膩體驗;(發現除繁瑣的直接實現外其他實現方式的可能性)
不妄自菲薄出身,用尊重的態度行動。(選擇回到經典二叉樹模式,試圖在舊傳統上建立新秩序)
知行合一,至此可謂正途。
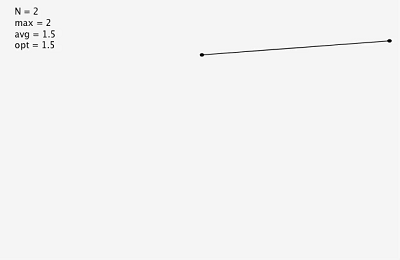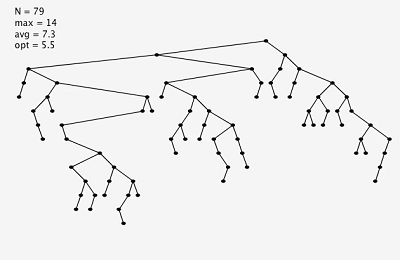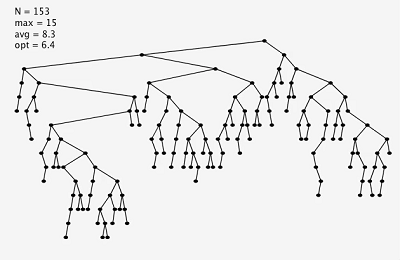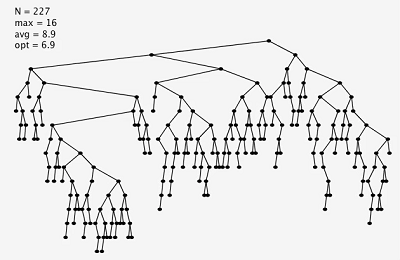
同為插入255個隨機節點,左圖為樸素二叉樹,右圖為左傾紅黑二叉樹。
作為第一部分的最後一個作業,kd-tree其實難度沒有它看起來那麼大。課程部分已很完整地討論過很多種經典的樹形結構(分析+實現),到這個階段學生應已對樹形結構非常熟悉了,實現kd-tree已是水到渠成。
同樣的,程式設計嚴謹性在這個作業中變得更加重要——情況相比前幾周又要複雜一些,從零編寫一個特定(且不簡單的)規則下執行的樹形結構,主要功能是高效地插入與查詢;
這次的作業同樣包含了一個暴力演算法的版本(使用預設的紅黑樹結構),除了在執行效率上可以做比較外,還提供了一個重要的軟體工程思路:面臨一個較為複雜,而優化空間很大的問題時,先實現一個最簡單的暴力演算法版本檢測結果(往往可以非常簡便地實現),再考慮進階的演算法與資料結構實現效能優化,並在實現期間,暴力演算法可以作為檢驗演算法正確性最直接的參考。
實現過程中值得提到的點:
節點的奇偶性是一個不小的麻煩,編寫需要十分謹慎,我的做法是在Node類中添加了一個boolean用以表示奇偶,相信一定有更好的方法(不儲存RectHV),還會回來探索;
Nearest Neighbor的查詢過程需要思考清楚,剪枝的界限十分清晰,尤其是剪裁其中一個子樹的條件:如果本子樹中找到的最近點與給定點距離 已小於 給定點到另一子樹矩形區域的距離(點到點距離比點到矩形距離還近時),才能跳過另一子樹的遍歷過程。
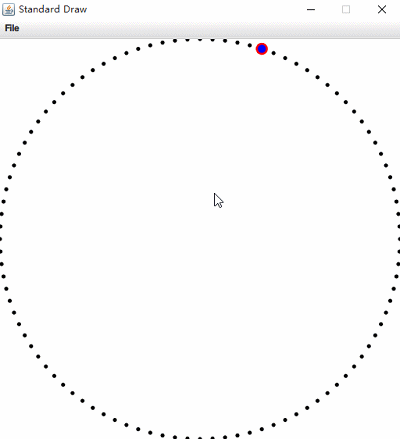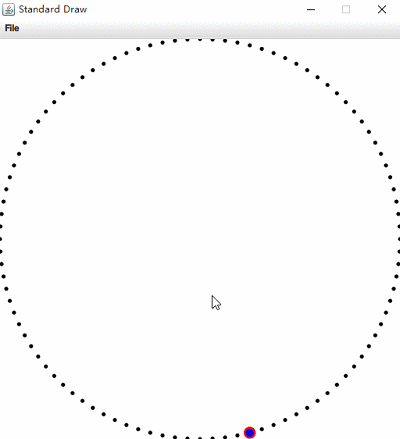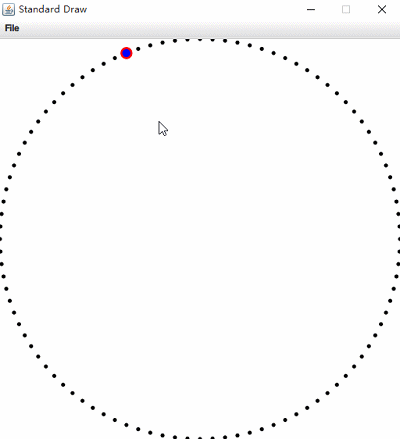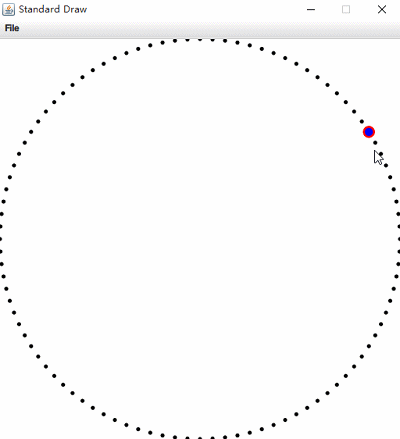
左圖為Nearest Neighbor,右圖為Range Search。(根據滑鼠狀態資訊)
圖中紅色部分為暴力演算法執行結果,藍色部分為kdtree執行結果;在增加資料量後單獨測試,暴力解法效率明顯下降。
-
在一個學期的辛苦努力後,帶著滿滿的收穫與日益成熟的頭腦,第二部分正式開始了。
“相信經過了第一部分的學習同學們都會有很大的提高,短暫休息後也恢復了飽滿的學習熱情,那麼我有理由相信你們準備好了接受點真正的考驗。” —— 視訊中永遠不會提到的導師內心獨白(歷經折磨後的腦補)
第二部分在課程與作業兩個方向的難度都比第一部分提升了一個檔次。好在不巧被導師言中,我的確有非常好的提升感和新一輪的熱情。
所以,放馬過來吧。
-
VI. Directed Graphs與WordNet √ 〇
第一週便直奔主題,開啟了資料結構領域的又一大領域:圖。
課程中出現了一個很有趣的分類值得提到,是形容演算法難度的:
1. 任何程式設計師都能夠做到。
2. 典型的勤奮的演算法課學生能夠做到。
3. 僱傭一個領域專家。
4. 非常難。
5. 沒有人知道難度。
6. 已證明不可能做到。
並舉出了一些符合條件例子來說明這些分類,當然可以料到的,有很多難度2的例子。
這針雞血打得,嘖嘖嘖,不留痕跡。
很好。諸位紅著眼的同學,準備變身吧。
第一週的作業是WordNet,少了第一部分作業多圖多動畫的喧鬧,不再為搏人眼球而吵吵嚷嚷,卻在安靜的terminal和腦中的抽象之海中展開了一場貨真價實的戰鬥。
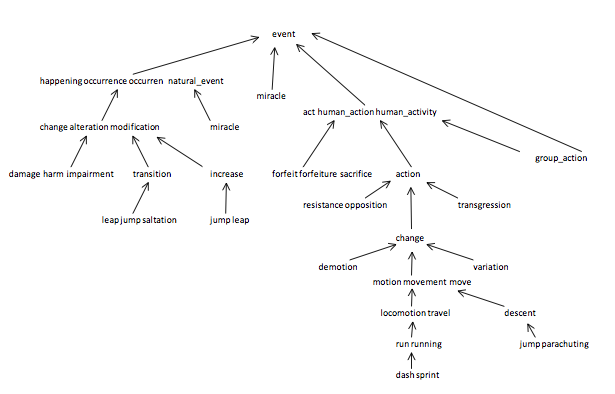
因文字方面中西文化背景截然不同,導致WordNet的概念不太方便簡單地描述清楚,但作業說明中已解釋得比較詳細,這裡只放一張示意圖:
整個作業可以分為三大部分:選擇合適的結構儲存結構複雜的詞典及其網路關係(基本功),實現正確高效的廣度優先遍歷計算SAP(難點),和在此基礎上一層一層更細緻的優化(進階);
本次也是checklist優化部分唯一標註optional的作業,因為的確實現起來有難度;分佈如上所注。
詞典(synsets)為ID與單詞的多對多關係(一詞多號,一號多詞,釋義僅供參考無需讀取),上下位關係(hypernyms)是以ID為單位的樹形結構(圖中的箭頭關係),可以明顯看出hypernyms使用有向圖表示,synsets儲存方式取決於訪問需求,因程式中正反都會使用(以詞求號,以號求詞,求詞存在),我選擇了空間換時間:
private ArrayList<LinkedList<String>> synset; // 以號求詞(獲取SAP中的ancestor對應的單詞)
private HashMap<String, LinkedList<Integer>> ids; // 以詞求號(獲取索引單詞的ID以計算SAP)
private HashSet<String> nouns; // 求詞存在(API需求功能)
private SAP sap; // 有向圖接著是SAP的實現,這裡周旋的餘地很大,一定要認真思考問題本質,並多考慮一些特殊情況檢測自己的想法,再開始下手去做,並如checklist所強調,不要輕易嘗試直接實現優化版本,因為細節繁瑣不易考慮周全,而可能帶來的潛在問題非常多,每實現一部分都要做周全的測試確保無誤才行。(儘管最終成功的優化,也可能僅僅是幾行的改變而已)
這裡要提到的點(細節):
在checklist提到的三個優化選擇中,我選擇了相對保守,但工作良好的優化方式:每次的搜尋初始化使用HashMap建構函式;正確實現了兩端同步執行的BFS,並提供了提前結束的出口;只快取了單個ID(單個節點與單個節點)的查詢結果;
對單ID快取的儲存方式,我的symbol table使用了一種很直接的無重合又簡單的hash計策:給定查詢ID為v與w,總ID數為V,則查詢結果的編號記為:
(V-1)+(V-2)+(V-3)+...+v+(w-v),化簡後為(V-1)*v-(v*v+v)/2+w。
提前結束BFS的出口開始時沒有考慮清楚,就暫時沒有新增,提交的版本拿到了103.12;後來仔細思考,發現了這部分餘地,僅增加了一行程式碼,分數便提高了不少;
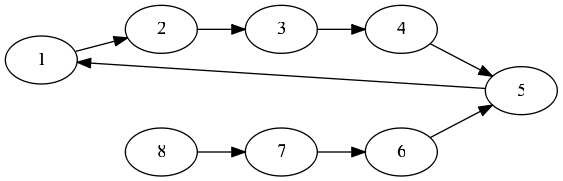
SAP同時支援DAG與DCG(有環圖),仔細分析如下這個特殊情況可能有助思考:(給定節點1與8,求其SAP)
BFS如由節點1先開始,則輪到第4次迭代時,節點1遍歷,發現共同祖先節點5,路徑距離為4+3=7,但此時不能停止搜尋;實際SAP的共同祖先為1,路徑距離為0+4=4,是在第4次迭代的節點8遍歷部分被發現的。
在這門課程的通用說明中便已提示過,不要把autograder當作debug的工具,以省去自己發現問題的過程;我必須保持誠實:至少,對於我這樣程式設計時基本“實用”精神至上的性格來講,因為autograder在各個方面都真的很完善,很多時候這是一條很難遵守的規定,所以我也體會到了這樣做的壞處:對於溫室中的作業來說有便利的autograder幫助簡直美好,但real world problem永遠是殘酷的;在這個作業中,我想我失去了一些很寶貴的機會,利用充足的測試材料親自去到那些資料的最深處遊蕩,去體會探索演算法的優劣,這個過程簡直是最迷人的部分(如上示例);意識到這些後,有一種作弊的愧疚感;每個人都應當正視它們,然後作出自己的選擇。
最終成績為106.25,具體Bonus點可以看這個檔案。
守得雲開見月明。
-
VII. Shortest Paths與Seam Carving √ 〇
本週作業算是一個“輕鬆有趣”的短暫休息;輕鬆到checklist都不知道該寫點什麼好了……
在第一部分結束後休息的階段,因為十分惦記完成這門課作業的快感,於是到booksite轉悠了好久,又完成了一些額外的專案;
而緊接著在booksite推薦的Nifty Assignment中便見到了這個作業,感覺很是驚豔,但還沒有動手做,沒想到這麼快就又見到它了。
(取自源SIGGRAPH2007介紹視訊,2008推出改進版)
作業中值得提到的點其實不多,大部分功能的實現都非常直接,中間加入了一點影象處理的入門知識,同樣也非常好理解,重點是最短路徑的BFS:
對於固定值邊界的處理比較繁瑣,需要仔細處理;
對很多影象處理問題,雖處理物件大體上還符合“圖”的定義,但因為很多影象固有的因素,會將問題簡化得多,不必再使用重量級的Digraph類,就事論事地解決問題即可;
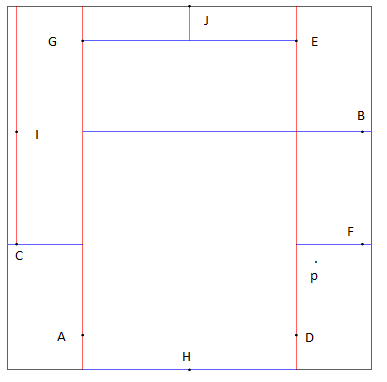
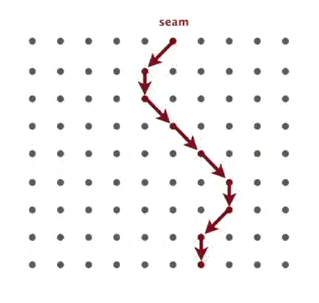
要找到能量最小的seam需要對整個影象計算路徑距離,我的做法是維護distTo(最近距離)和edgeTo(最近距離對應“父節點”)兩個陣列,遍歷全圖後在最後一行(列)找到distTo的最小值即為所求seam的尾元素,通過追蹤edgeTo即可得到所求seam。energy的複用是一個小難點,需要認真考慮每移除一列或一行seam後,哪些情況下的點應該被重新計算,參考作業說明的vertical-seam.png、horizontal-seam.png或下圖去分析,可能會有幫助:
我想到的轉置的目的是為了在縱橫兩個方向都能利用System.arraycopy()的高效,開始時我沒有做這項優化,是手寫了removeHorizontalSeam()的這個過程,因已達到了滿分要求便沒有再優化。
-
MaxFlow將是本課程接觸的最複雜的圖論問題了。別這樣,我才剛剛興奮起來……
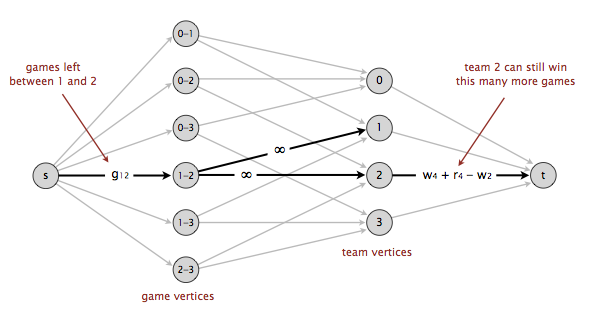
同樣地,作業Baseball Elimination是一個非常巧妙的Maxflow應用,甚至都與“流量”沒有任何關係:
根據實時賽季資料,通過建立流量模型,判斷當前局勢是否已出現被“數學上淘汰”的隊伍(已無法再獲得冠軍);
雖然演算法上十分有趣,但個人並不喜歡這道題背後某個方向的思維:對辛苦奮戰的運動員來說,每場比賽都是戰鬥,每個細節的表現才定義了自己,不是由一群snobbish的“科學家”說你被“數學上淘汰”了,你就真的毫無希望了;
當然同時要明白這只是“黑暗版”的理解,對於專業選手來講任何資訊都有其價值,在賽前以最清楚的資料明確自己的處境,以更好地調整戰略、激勵人心,再參與比賽,才算是真正在現實世界用出了好演算法的最大價值。
Again, all in all,要nerdy地熱愛,但不要做nerd。
同如修行的和尚,功德要回向眾生,而禪喜,留給自己就好。
本次作業在細節上有一些非常簡單的小技巧可以幫助簡化實現(簡潔性也是checklist提示的,參考程式碼不到200行,我的版本為150行左右),但可能不是第一次思考時就能想到:
在讀取檔案資料時就可額外計算(儲存)一些後期需要的資料:目前榜首隊伍與獲勝場數(用於簡單淘汰),和以雙方隊伍為單位的比賽場次(用於建立FlowNetwork的頂點數);
“Do not worry about over-optimizing your program because the data sets that arise in real applications are tiny.” 對我的思路,這意味著無需考慮FlowNetwork的複用問題——一個早期造成很多痛苦的優化嘗試;
FordFulkerson類的使用實際上使問題僅剩下了建模部分,且在說明中已解釋得非常詳細,故實現十分直接。
-
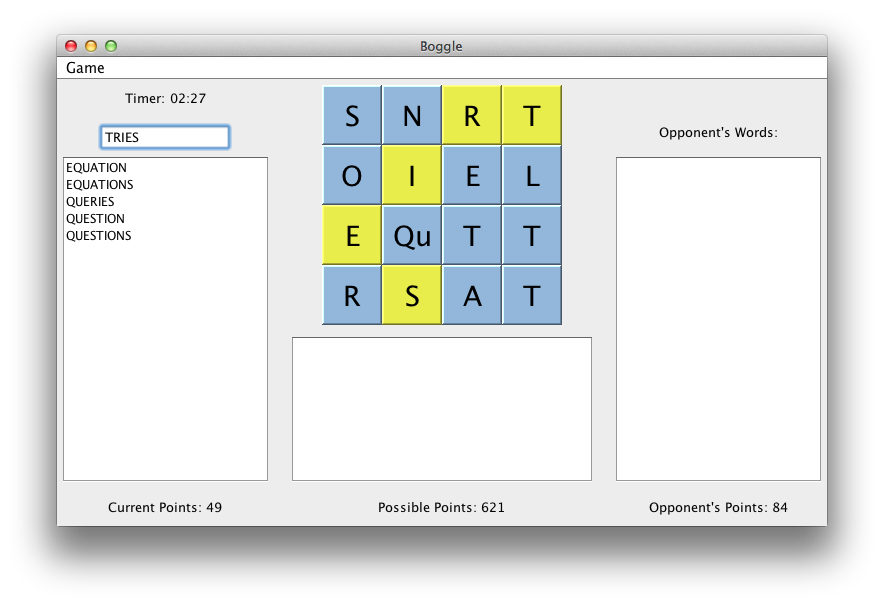
然而Boggle卻是第二部分課程作業中,最有挑戰性的一個。(因為我沒有拿到Bonus T_T)
“The goal on this assignment is raw speed—for example, it's fine to use 10× more memory if the program is 10× faster. ”(“明確地”暗示使用Trie)
從動手開始做本次作業,到基本感到沒有優化餘地,我的程式碼經歷了大概4-5個大版本的改變,小的修正與優化更是不計其數,即使是這樣一個固定情形下的問題,也令我好好體會了一次,程式迭代更新、不斷修正與優化的過程。
本次任務相當於編寫圖示遊戲的AI部分——BoggleSolver,而要拿到滿分以至Bonus,需要一秒內解決成千上萬個Boggle Board。
下面是我經歷的迭代過程的簡短介紹:(只選出了幾個典型版本,括號內為autograder針對getAllValidWords()的時間測試,值為5秒內呼叫次數的reference / student ratio,越小越快;滿分要求小於2,Bonus要求小於0.5;源材料沒有保留完整,資料可能稍有出入)
很遺憾最終依然沒有拿到Bonus,但每一份效能都已是得來不易。一版(~2.5):簡單更改庫中現成的TST(三叉搜尋樹)類(增加一個單行的PrefixQuery小函式),將Board預處理為char[W*H][9],使用非遞迴方式的DFS(主要維護兩個stack)遍歷Board實現;
二版(~1.6):在前版基礎上,改TST為手寫實現的26-way Trie類,Board預處理為Bag<Integer>[W*H],所有函式都為非遞迴方式實現(如checklist所要求);
三版(~0.8):在前版基礎上,改非遞迴方式DFS為遞迴,將Trie類內容直接寫入BoggleSolver,在DFS過程中直接傳遞Node指標而非呼叫PrefixQuery函式;
終版(0.55):在前版基礎上,全面整理了各步驟細節,cache中間變數,使用Bag而非HashSet儲存查詢結果,及(參考論壇討論後)其他細節上的技巧性優化。
Test 2: timing getAllValidWords() for 5.0 seconds using dictionary-yawl.txt
(must be <= 2x reference solution)
- reference solution calls per second: 6175.83
- student solution calls per second: 11200.52
- reference / student ratio: 0.55
學習經驗:
開始時其實比較抗拒自己實現一些工具類,如TST或Trie,除了必要的功能外很不願意改動它們;但當完成前期版本,開始尋求效能優化,實實在在地瞭解了這些工具類運作機理後,才發現最大的障礙其實來自這些工具類“為通用性而做出的效能上的犧牲”,於是義無反顧地自己手動實現了滿足“最低需求”的版本,但因細節盡在自己的掌握,使得在DFS中傳遞Node指標這樣最直接有效的實現方式變得可能,自然,也得到了對應的回報;
checklist也不是聖經,有獨立思考問題的意識才可能發現更大的世界:在實現非遞迴版DFS時明顯感到比較吃力,同時需要追蹤維護很多變數,而DFS的邏輯本身也更適合遞迴;非遞迴版DFS全當練手,而能夠轉回遞迴實現版本則是大膽獨立思考的結果;
有同學使用多執行緒達到了非常快的成績(0.24),但在演算法課程作業這個意義上,多執行緒其實尚處於“灰色區域”,有作弊的嫌疑——況且也沒什麼技術含量,無須在意。
-
如果要用一個詞來形容這次的作業,我想這個新學的fancy word會再合適不過,“Nifty”。
課程講到這周基本接近尾聲,正則表示式沒有作為重點分析太多,而資料壓縮,則成為了這最後一次作業的主題;它看似無趣,卻在作業細緻入微的步驟上隱藏著許多非常精緻的點,其間如抽絲撥繭般細膩的過程,堪稱快感連連;而其中一個Circular Suffix Array(CSA)排序的實現,可以涵蓋從第一部分起討論過的所有排序演算法:題目本身並沒有任何限制;學生需要認真比較每一種排序方式的優劣,並選擇出其中一種或幾種方法的組合,重新制造出一個最適合當前情況下的高效解決方案;在這個意義上,它相比前面的作業,與real world problem更接近了一步。
資料壓縮的過程本身就是比較抽象的,而這次的作業說明與checklist更是文字翻倍而全無附圖,有同學開始時看不懂題目也是正常,慢慢來啦。【下文所有中括號為題目簡短說明,推薦閱讀詳細說明】
i Original Suffixes Sorted Suffixes t index[i] -- ----------------------- ----------------------- -------- 0 A B R A C A D A B R A ! ! A B R A C A D A B R A 11 1 B R A C A D A B R A ! A A ! A B R A C A D A B R 10 2 R A C A D A B R A ! A B A B R A ! A B R A C A D 7 *3 A C A D A B R A ! A B R A B R A C A D A B R A ! *0 4 C A D A B R A ! A B R A A C A D A B R A ! A B R 3 5 A D A B R A ! A B R A C A D A B R A ! A B R A C 5 6 D A B R A ! A B R A C A B R A ! A B R A C A D A 8 7 A B R A ! A B R A C A D B R A C A D A B R A ! A 1 8 B R A ! A B R A C A D A C A D A B R A ! A B R A 4 9 R A ! A B R A C A D A B D A B R A ! A B R A C A 6 10 A ! A B R A C A D A B R R A ! A B R A C A D A B 9 11 ! A B R A C A D A B R A R A C A D A B R A ! A B 2
【encode部分:對源字串的CSA(左)排序,返回排好序的CSA(右)的最後一列(ARD!RCAAAABB),及源字串所在位置(3)。】
認真閱讀作業材料即可大致瞭解,Burrows-Wheeler壓縮演算法的三部分:
Huffman壓縮已實現不必關心;
Move-to-front編碼最為簡單可直接實現;
Burrows-Wheeler decoder被稱為“the trickest part”,但緊接著便已提示到key-indexed counting與10行的核心程式碼長度,其實已算是提示了很多;
而其encoding需要使用Circular Suffix Array,所以最大的課題其實是,如何以最高效率實現Circular Suffix Array排序。
下面就先來看CSA的排序問題:
因由源字串逐個迴圈偏移構成,CSA是一種具備很多特殊性質的陣列,而對這樣的陣列排序照搬通用的排序演算法一定有很大的優化空間沒有利用,因此手工打造一個高效實用“特別化”的排序演算法,就變成了眼前最實際的問題。
有上一週迭代更新的經驗在前,這次幾乎是立即開始了手工打造的過程,而可考慮的範圍又幾乎沒有限制,以下是我的幾個正確版本:(分數為CSA建構函式執行時間的student / reference ratio(越小越快),均取資料長度為409600的測試成績作為樣本;兩個分數僅輸入資料不同,第一個為隨機ASCII,第二個為典型英文內容(dickens.txt);滿分要求均為3以下)
一版(2.85,5.16):統一使用Mergesort;
二版(4.07,6.69):統一使用Comparator暴力比較(或封裝為Comparable類,效率接近);
三版(0.45,1.34):長度15以下切換到insertion sort,以上使用MSD radix sort;
四版(1.29,1.87):長度15以下切換到insertion sort,以上使用3 way radix quick sort;
五版(3.04,3.83):改編自booksite所附原始碼,較為低效的ManberMyers實現(使用MSD排好首位字元,接著使用簡單quicksort);
這幾個是在權衡利弊後選擇實現(如沒有選擇LSD),並已保證正確性的版本(其中不少的實現使用了algs4.jar原始碼),可以看出目前相對最高效的方案是MSD+insertion;
因對課堂中提到的ManberMyers演算法很感興趣,所以後期做了不少嘗試,但還是沒有完全原創地完成一個正確版本,加上還有很多好的選擇,這裡還會繼續努力;
課程API對Java的static塊沒有要求,所以可以在合適處(如MoveToFront類)利用。
最後是本作業最“Nifty”的部分,Burrows-Wheeler decoder:
i Sorted Suffixes t next -- ----------------------- ---- 0 ! ? ? ? ? ? ? ? ? ? ? A 3 1 A ? ? ? ? ? ? ? ? ? ? R 0 2 A ? ? ? ? ? ? ? ? ? ? D 6 *3 A ? ? ? ? ? ? ? ? ? ? ! 7 4 A ? ? ? ? ? ? ? ? ? ? R 8 5 A ? ? ? ? ? ? ? ? ? ? C 9 6 B ? ? ? ? ? ? ? ? ? ? A 10 7 B ? ? ? ? ? ? ? ? ? ? A 11 8 C ? ? ? ? ? ? ? ? ? ? A 5 9 D ? ? ? ? ? ? ? ? ? ? A 2 10 R ? ? ? ? ? ? ? ? ? ? B 1 11 R ? ? ? ? ? ? ? ? ? ? B 4【decode部分(層層相扣,建議讀原文):已知CSA最後一列(ARD!...),與源字串所在行(3);對最後一列排序可得第一列(!AAA...);而next陣列使用方式如下:因已知源字串(排序前第0行)在排序後位置為3,而next[3] = 7,即排序後第7行(B...A)為排序前的第1行(第0行的下一行),可知源字串第1位為'B'(根據第3行,第0位為‘A’),依此類推即可得到源字串;next陣列的構造為通過比較首尾字元出現位置得到:如第i行末位為A,而首位第一個未標記過的A出現在第j行,則next[i] = j,標記第j行。】
開始時我只看了作業說明,所以冒失地寫好了一個“暴力decode”還渾然不自知,直到參考checklist後:“WTF”
事實證明那10行核心程式碼基本與下圖所示相同:
問題的關鍵在於next陣列的構造,可總結為如下幾點:
於是在對原始碼極簡單的改變後,完成了截然不同的任務:(spoiler alert)key-indexed counting核心機理是index的累加,可以保證排序結果的穩定(stable);
根據作業說明的分析,next陣列構建的過程,確定重複字元位置的核心機理也是“穩定性”(針對多次出現的同一字元,首尾列的相對先後順序一致);
對CSA可以不顯式建立字串陣列而僅保留源字串,只新增一個簡單的根據offset和index迴圈獲取對應字元的工具函式即可,這為直接使用key-indexed counting創造了非常好的環境。
for (int i = 0; i < N; i++)
count[t[i]+1]++;
for (int i = 0; i < 256; i++)
count[i+1] += count[i];
// The trickiest part
for (int i = 0; i < N; i++)
next[count[t[i]]++] = i;6行完成了next陣列的構建,加上接下來還原源字串的過程,達到10行。
仔細品讀其中內容至理解透徹,相信這妙不可言的感覺一定已深深印在閣下腦海。
歡迎來到演算法世界。
-