【貪心演算法】Huffman編碼
問題描述
有一組字符集{c1, c2, …, cn},在使用這組字符集的過程中,通過統計發現每個字元都有其相應的出現頻率,假設對應的頻率為{f1, f2, …, fn}。現在需要對這些字元進行二進位制編碼,我們希望的編碼結果如下:每個字元都有其獨一無二的編碼;編碼長度是變長的,頻率大的字元使用更少的二進位制位進行編碼,頻率小的字元則使用比較多的二進位制位進行編碼,使得最終的平均編碼長度達到最短;每個字元的編碼都有特定的字首,一個字元的編碼不可能會是另一個字元的字首,這樣我們可以在讀取編碼時,當讀取的二進位制位可以對應一個字元時,就讀取出該字元。舉個例子,假如我們有字符集{‘a’, ‘b’, ‘c’},字元’a’的編碼為001,字元’b’的編碼為010,那麼此時c的編碼不能為00或者01,這樣我們才能識別’a’和’c’或者’b’和’c’。
演算法描述
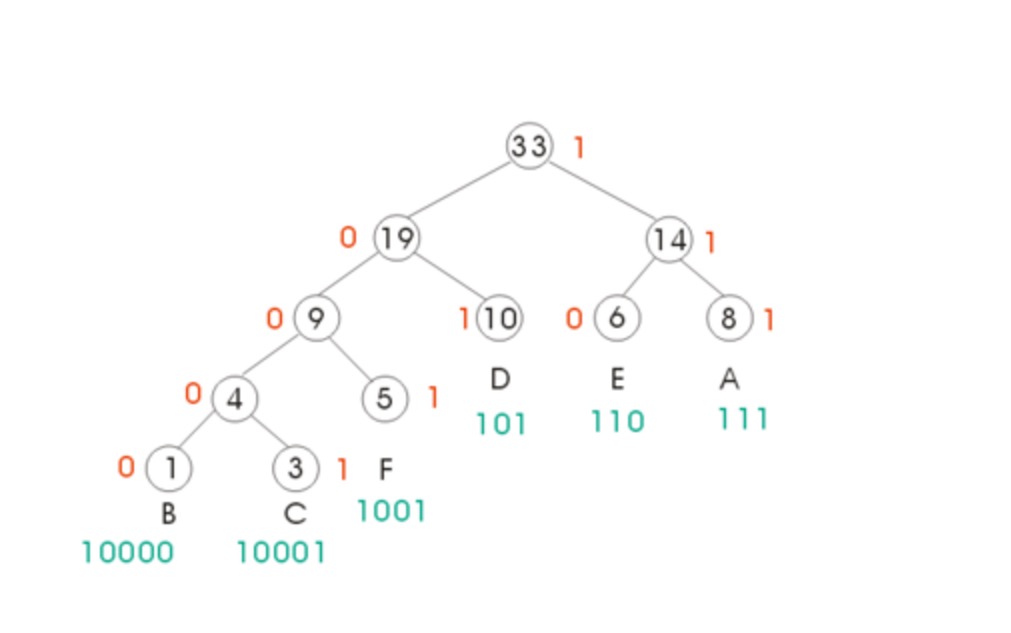
上述問題可以使用Huffman編碼來解決,Huffman編碼實際上是一個貪心演算法。在這個演算法中,使用二叉樹來表示字首碼,每個字元都是樹的葉子結點,非葉子結點則不代表任何字元。將每個字元構造成結點形成結點集S,每次都從結點集S中選出頻率最低的兩個結點x和y作為子節點進行建樹,為這兩個子結點構造一個父節點,父節點不儲存任何字元,父節點的頻率為兩個子節點頻率之和,將兩個子節點從S中移走,將父節點加入S中。不斷迭代下去,直到S只剩一個結點時,這個結點就是樹的根節點。這樣我們就得到了一棵Huffman樹,整個過程就是一個自底向上的建樹過程。由於從根節點到每個葉子節點有且僅有一條路徑,所以,每個葉子的路徑都是不一樣的,唯一的。我們把從根節點到葉子節點的路徑記錄下來,便可作為葉子節點上字元的編碼。初始化編碼為空,從根節點開始,往左走則編碼加0,往右走則編碼加1,具體展示圖如下所示:
建樹過程的虛擬碼如下:
給定字符集C={c1,c2,...,cn},每個字元ci都有相應的頻率fi
根據字符集構建結點集S={s1,s2,...,sn},每個結點si儲存有字元ci和頻率fi的資訊
while |S| != 1 do
取出S中頻率最小的兩個結點x和y;
構造父節點z;
z.f = x.f + y.f;
z.c = undefined;
z.left = x;
z.right = y;
將x和y從S中移走,將z加入S;
endWhile
此時S[0]就是根節點,返回根節點最後整個Huffman編碼過程的C++實現如下(建樹+編碼):
#include <iostream>