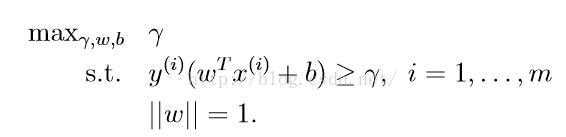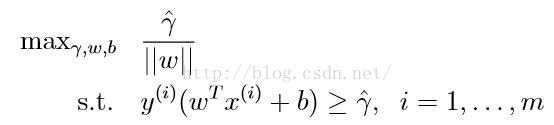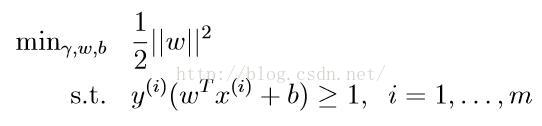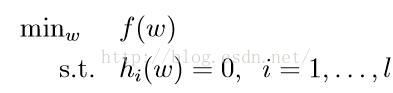【七】最優間隔分類器問題
最優間隔分類器 the Optimal Margin Classifier
在上一講內容中,我們介紹了函式間隔和幾何間隔,我們也對比了這兩種間隔的差異。我們希望可以得到更小的幾何間隔。一個直觀的優化方程是
上述方程中γ即為幾何間隔,注意到我們限定了||ω||=1,這表明幾何間隔和函式間隔是相同的。但這一優化問題很難求解,因為它是非凸的,我們不能利用已有的優化程式進行求解。所以我們將優化問題轉化為另一種方程,如下
此時我們將對||ω||的限制移入目標方程中,這是我們的目標方程實際上就是幾何間隔,除以||ω||起到了歸一化的作用。此時我們已經可以使用現成的程式求解,但這一優化問題包含了兩個引數,γ和ω。顯然引數越少求解越方便,我們希望有一種方法可以減少引數。由於我們幾何間隔是我們希望得到的最小間隔
注意到我們從求目標函式的最大值轉為求最小值,這是因為在原方程中ω位於分母的位置;同時我們求的值為1/2||ω||^2,這與||ω||的增減性相同,使用平方項是為了方便求導。此時的方程已經可以通過任意一種求解優化問題的演算法解出,如二次規劃演算法。這一優化為題的解成為最優間隔分類器。
拉格朗日對偶 Lagrange Duality
假如我們要求解如下優化問題(注意到此時約束條件均為等式)
則我們可定義拉格朗日方程為
,其中βi稱為拉格朗日乘子(Lagrange Multipliers)
。我們可以通過設定導數為零的方式求得ω和β
下面我們將拉格朗日演算法應用到最優間隔分類器中,我們稱如下問題為原始(Primal )問題
為了利用拉格朗日演算法解決上述問題,我們定義生成拉格朗日方程(Generalized Lagrangian)為
其中α和β都稱為拉格朗日乘子,這時我們定義下列方程(其下標p表示原始primal)
可以得出當其不滿足約束條件時,其可取到無窮大
因此我們可以得出下列方程
因此最優間隔分類器的目標函式為
因此,我們使用
代表原始問題的目標函式
這時我們定義方程
其中的D表示對偶Dual
注意到原始方程是對α和β進行優化得到最大的L方程值,而此方程是取使L最小的ω,因此我們可以定義對偶優化問題
這與我們之前定義的原始優化方程只有求最大值和最小值的順序不同,我們定義
我們可以得出d*和p*的關係如下(注意L為一個凸函式)
在某一條件下,我們可以取到d*=p*,下面我們將討論這一情況具體是什麼。
KKT條件 Karush-Kuhn-Tucker Conditions
假設方程f和gi均為凸函式,並且hi為一個對映,假設存在一ω對於任意i使gi(ω)<0。
在上述假設中,假設存在ω*為原式方程的最優解,α*、β*為對偶問題的最優解,並且若有
,則ω*、α*、β*必滿足如下條件,稱之為KKT條件(Karush-Kuhn-Tucker Conditions)
這表明,只要存在ω*、α*、β*滿足KKT條件,則一定存在d*和p*的解。我們需要特別注意的是,上述第三個方程
稱為KKT對偶互補條件 KKT Dual Complementarity Condition。這一條件指出,αi和gi至少有一項取值為0。考慮到實際意義,當gi(ω)=0時表示這一點位於距離分界超平面幾何間隔為1的位置上(詳細見下文推導)。
將上述拓展至支援向量機中,我們可以將約束條件寫為,注意到我們只對函式間隔為1的訓練資料可能有αi.>0。如下圖所示
距離分介面最近的點為1,即有三個點(兩個正值,一個負值)位於平行於分介面的虛線上。這三個點稱為支援向量 Support Vectors。在實際使用中,支援向量的個數一般會比訓練集的規模小很多。
我們將拉格朗日演算法應用到SVM中,可得拉格朗日方程為
為了通過對偶問題求解,我們需要首先計算L的最小值,為此我們需要先對ω和β求導,並令導數為零
對ω有
同理我們對β求導得
將上述兩個等式代入拉格朗日方程中並化簡為
我們推導上述方程是通過選擇ω和β取得L最小值求得的,為了完成對偶問題,我們定義下列優化問題
已知可證明SVM問題滿足KKT條件,因此解決了上述優化問題可得到α的值,至此我們已求得ω*、α*、β*的值,b在SVM中可視為一個常量,它可通過以下等式計算出
此時我們已解決了對偶問題,即等價的解決了原始問題。
因此當給定一個測試資料x時,我們將上述求出的ω和b代入SVM的計算函式,如下
由之前的推導我們已經知道,對於大多數訓練集資料,其對應的αi為0,因此期第一項為0,我們只需考慮少數αi不為零的訓練向量(即支援向量)即可,此時影響計算的只有測試資料x和支援向量的內積。
//這裡是分割線~
//順便給自己的公眾號打個廣告,希望大家多多關注~
//關注我的公眾號可以看到更多有意思的東西哦~