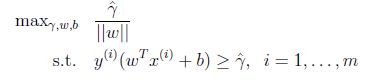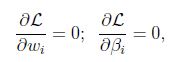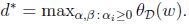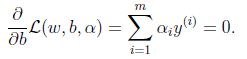【斯坦福---機器學習】複習筆記之最優間隔分類器
本講大綱:
1.最優間隔分類器(optimal margin classifier)
2.原始/對偶優化問題(KKT)(primal/dual optimization problem)
3.SVM對偶(SVM dual)
4.核方法(kernels)(簡要,下一講詳細)
1.最優間隔分類器
假設給我們的資料集是線性可分的(linearly separable). 就是說用超平面可以分隔正負樣本. 我們要找到最大的幾何間隔. 我們可以轉化為下面的優化問題:
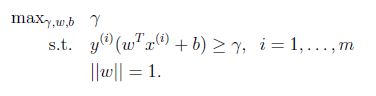
由於||W|| = 1,這保證了函式間隔等於幾何間隔,只要解決了上面的優化問題我們就解決了這個問題,但是||W||是一個不好的(非凸性)的限制,這不是我們能夠直接用軟體解決的優化問題. 因此轉化為更好的一個問題:
我們最大化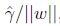
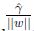
前面有討論過對w和b加上任意比例的限制不會改變什麼. 因此,加上規模的限制,對訓練集的函式間隔設定為1: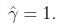
因此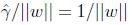
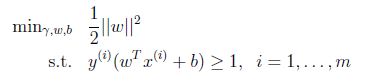
上面的優化問題變為一個凸二次目標函式(convex quadratic objective). 這給我們一個最優間隔分類器的解決方案. 這個優化問題可以用商用的二次程式設計程式碼解決.
2.原始/對偶優化問題
2.1 拉格朗日二元性(Lagrange duality)
考慮下面形式的問題:
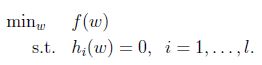
我們可以用拉格朗日乘數法來解決這個問題.
定義Lagrangian為:
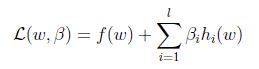
這邊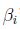
然後解出w和
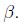
2.2 原始優化問題(primal optimization problem)
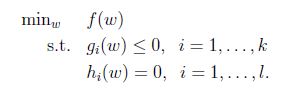
定義一般的拉格朗日運算元(generalized Lagrangian):
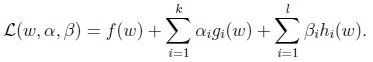
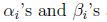
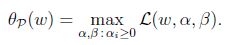
下標”P”表示”prime”, 如果給定的w違反了原始限制(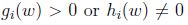
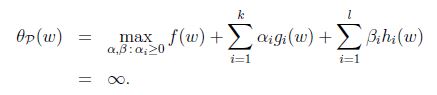
如果w滿足原始限制,那麼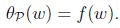
考慮最小化問題:
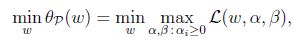
可以看到回到了最初的原始問題. 定義目標的原始值為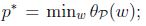
一個略微不同的問題:
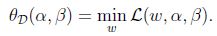
下標”D”表示”dual”.
2.3 對偶優化問題(dual optimization problem)
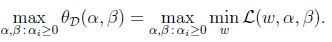
同樣的,定義目標的對偶值為:
顯然: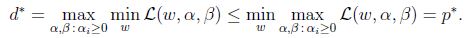
(函式最小值的最大值肯定小於等於最大值的最小值
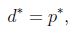 ,因此我們可以通過解決原始問題來解決對偶問題.
,因此我們可以通過解決原始問題來解決對偶問題.
假設f和g是凸函式(黑塞矩陣為半正定的),h為仿射函式(affine,和線性是一樣的,只不過是加了截距,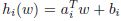
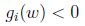
基於上面的假設,肯定存在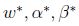
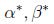
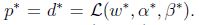
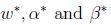
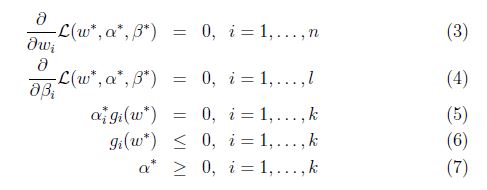
如果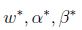
等式(5)稱為KKT對偶補充條件(KKT dual complementarity condition). 具體來說,就是如果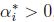
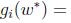
3.SVM對偶
前面為了找到最優間隔分類器,提到以下的優化問題(原始優化):
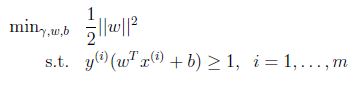
限制可以寫為:
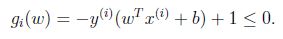
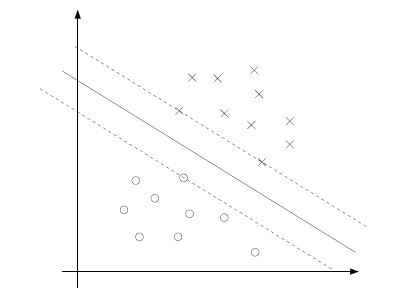
(實線為超平面)
最小的間隔是離決定邊界最近的點,上圖中有三個(一個負的兩個正的),因此對於我們的優化問題只有三個a是不等於零的. (KKT對偶補充條件,只有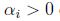
為優化問題構建Lagrangian,有:
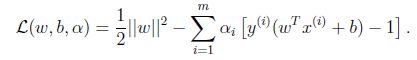
對w求偏導:
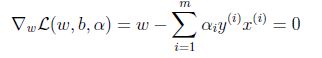
推出:
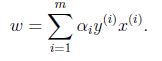
對b求偏導:
根據上面的式子化簡得到:
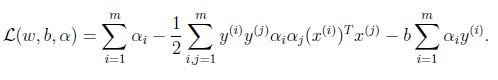
最後一項為零,進一步得到:
得到以下對偶優化問題:
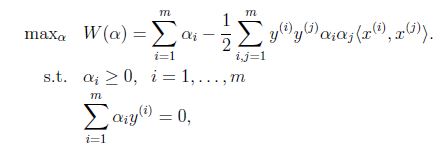
需要滿足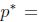
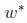
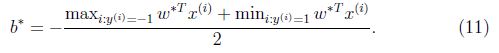
再得到:
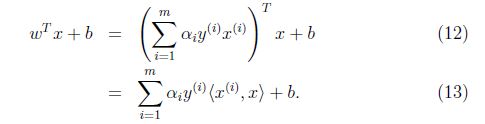
因此如果我們找到了a,為了預測,我們只需要計算x和資料集中點的內積(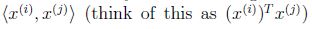
4.核方法
有時候訓練樣本的維數很高,甚至有可能得到的特徵向量是無限維的. 通過計算不同方法的內積,利用內積來進行有效的預測.