NOIP2017普及組複賽題解
T1 score 題面:
(不想看的跳過吧)

無疑,這是一道可以媲美A+B Problem的大水題,剛開始看到,以為要用浮點數操作之類的,但是題目給出A,B,C全部小於等於100並且都為10的倍數,所以就使這道題變成了徹徹底底的水題。
題意大概如此:給出三個均為10的倍數並且小於等於100的整數A,B,C,以整數形式輸出
顯然
為什麼要這樣算呢,因為這樣能夠避免浮點數運算,粗心出錯的概率也就小了很多,下面是程式碼:
#include <cstdio>
int (真的需要給這題題解嗎?)
T2 librarian 題面
(不想看的跳過吧)


剛開始看,以為是什麼有套路的題目,實際上就是一道模擬。
題意:有一個n個元素的字典,元素都是整數,給出q個詢問,每個詢問有一個十進位制下長度為a的整數b,求字典的n個元素中在十進位制下,後a位與b相等的元素中,字典序最小的一個,如果沒有則輸出-1。(其實不如看題面)
思路:模擬
首先讀入n個整數,沒有必要以字串形式讀入,當然字串也可以做。
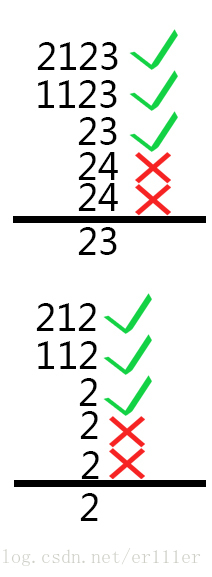
那麼對於每一個整數b(a其實是沒有用的),我們設一個p[i],p[i]=1表示a[i]不以b結尾,即不符合要求;其餘的p[i]=0就是符合條件的。那麼剩下的工作就是把n個元素中滿足p[i]=0的元素取一個最小值,問題就轉化為了如何求p陣列。具體步驟:將b與其它幾個a[i]末尾對齊,此時b的最後一位為b mod 10,a[i]的最後一位為a[i] mod 10,顯然在(b mod 10)和(a[i] mod 10)不相等時,p[i]=1,然後就把b和a[i]同時/10,移動到下一位比較,直到b為0為止。比較過程如下:
(題目資料中23的比較)
(題目資料中123的比較)
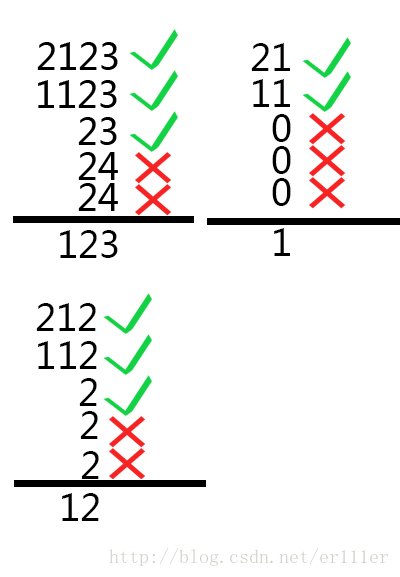
時間複雜度為O(nq),題目資料顯然不會超時。
程式碼:
#include <cstdio>
#include <cstring>
const int N = 1007, INF = 666666666; //個人習慣,別在意哈
int n, q, a, b, ans = INF;
int num[N], t[N], p[N];
int main()
{
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++)
scanf("%d", &num[i]); //以整數形式讀入資料 T3 chess 題面
(一定要認真看!!!)



剛看到的時候覺得好煩,本來是沒打算做的,後來為了水點分,打了dfs+剪枝,竟然90,丟的10分是低階錯誤,事實證明還是要敢做敢想。
題意:在一個m*m的矩陣上,求(1,1)到(m,m)的最低花費,移動的規則如下:
1.棋盤上有n個格子有顏色,顏色為紅色或黃色,其餘皆為無色。
2.每次移動僅能向上下左右四個相鄰的格子移動。
3.(x1,y1)移動到(x2,y2)的必要條件是(x1,y1)和(x2,y2)都有色。
3.如果(x1,y1)和(x2,y2)都有色並且顏色相同,則花費為0。
4.如果(x1,y1)和(x2,y2)都有色並且顏色不同,則花費為1。
5.如果(x2,y2)為無色的,則可以花費2使得(x2,y2)變為一個紅黃中任意一種顏色然後走過去,在走上原本就有顏色的格子前,不能再次使一個格子變色。
6.第3條相當於每次站立的點必須有色。
思路:dfs+剪枝 OR bfs+最短路
dfs+剪枝:
我們可以設一個
1.(dx,dy)越界,此時直接return。
2.(dx,dy)無色,那麼此時就將(dx,dy)變為與(x,y)同色(以保證花費最小),然後遞迴到dfs(dx, dy, 0),記得返回時將(dx,dy)回溯為無色。
3.(dx,dy)有色且與(x,y)顏色相同,此時直接走至dfs(dx, dy, 1)。
4.(dx,dy)有色且與(x,y)顏色不同,此時直接走至dfs(dx, dy, 1)。
但是這樣有一個問題,那就是可以能出現兩個點一直互相跳,陷入死迴圈的局面。考慮情況2,如果
程式碼:
#include <cstdio>
#include <cstring>
const int N = 107, D[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; //可擴充套件的節點
int a[N][N], f[N][N]; //a為顏色陣列,-1表示無色,0和1表示其他顏色
int n, m, x, y, c;
inline int hf(int x, int y) { return (x <= n && x > 0 && y <= n && y > 0); } //判斷座標是否合法(hf)
void dfs(int x, int y, int tag) //搜尋
{
for (int i = 0; i < 4; i++)
{
int dx = x + D[i][0], dy = y + D[i][1]; //擴展出節點(dx,dy)
if (hf(dx, dy)) //跳過不合法的節點
{
if (a[dx][dy] == -1) //(dx,dy)無色的情況
{
if (f[x][y] + 2 < f[dx][dy]/*如上文所說剪枝*/ && tag/*可以變色*/)
{
f[dx][dy] = f[x][y] + 2; //更新f陣列
a[dx][dy] = a[x][y]; //變色
dfs(dx, dy, 0); //tag改為0
a[dx][dy] = -1; //回溯
}
}
else if (a[dx][dy] == a[x][y]) //有色且顏色相同
{
if (f[x][y] < f[dx][dy]/*上文所述剪枝*/)
{
f[dx][dy] = f[x][y]; //更新
dfs(dx, dy, 1); //走至(dx,dy)
}
}
else if (a[dx][dy] != a[x][y]) //有色且顏色不同
{
if (f[x][y] + 1 < f[dx][dy]/*上文所述剪枝*/)
{
f[dx][dy] = f[x][y] + 1; //更新
dfs(dx, dy, 1); //走至(dx,dy)
}
}
}
}
}
int main()
{
memset(a, -1, sizeof(a));
memset(f, 0x3f, sizeof(f)); //賦為無窮大
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &x, &y, &c);
a[x][y] = c;
}
f[1][1] = 0; //(1,1)為出發點,距離自然為0
dfs(1, 1, 1);
if (f[n][n] == 0x3f3f3f3f) //無法到達
printf("-1\n");
else
printf("%d\n", f[n][n]);
return 0;
}
bfs+最短路:
看到矩陣AND最小,很自然地想到最短路,思路與SPFA差不多,只是dis要多設一維表示顏色,其餘做法同SPFA,程式碼:
#include <cstdio>
#include <cstring>
struct point { int x, y, col, tag; };
const int N = 107, D[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int a[N][N], dis[N][N][2], vis[N][N][2][2];
point que[N * N * 10]; //多乘一點保險
int n, m, x, y, c, head = 1, tail= 0;
inline int hf(int x, int y) { return (x <= n && x > 0 && y <= n && y > 0); } //合法
inline int min(int a, int b) { return a < b ? a : b; } //自定義min函式,比STL不知道快多少
int main()
{
memset(dis, 0x3f, sizeof(dis)); //初始化無窮大
memset(vis, 0, sizeof(vis));
memset(a, -1, sizeof(a));
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &x, &y, &c);
a[x][y] = c;
}
que[++tail] = (point){1, 1, a[1][1], 1};
dis[1][1][a[1][1]] = 0, vis[1][1][a[1][1]][1] = 1;
while (head <= tail)
{
point tmp = que[head++];
vis[tmp.x][tmp.y][tmp.col][tmp.tag] = 0; //標記出隊
for (int i = 0; i < 4; i++) //擴充套件節點
{
int dx = tmp.x + D[i][0], dy = tmp.y + D[i][1];
if (hf(dx, dy))
{
if (a[dx][dy] == -1)
{
if (dis[tmp.x][tmp.y][tmp.col] + 2 < dis[dx][dy][tmp.col] && tmp.tag)
{
dis[dx][dy][tmp.col] = dis[tmp.x][tmp.y][tmp.col] + 2;
if (!vis[dx][dy][tmp.col][0])
{
que[++tail] = (point){dx, dy, tmp.col, 0};
vis[dx][dy][tmp.col][0] = 1;
}
}
}
else if (a[dx][dy] == tmp.col)
{
if (dis[tmp.x][tmp.y][tmp.col] < dis[dx][dy][tmp.col])
{
dis[dx][dy][tmp.col] = dis[tmp.x][tmp.y][tmp.col];
if (!vis[dx][dy][tmp.col][1])
{
que[++tail] = (point){dx, dy, tmp.col, 1};
vis[dx][dy][tmp.col][1] = 1;
}
}
}
else if (a[dx][dy] != tmp.col)
{
if (dis[tmp.x][tmp.y][tmp.col] + 1 < dis[dx][dy][a[dx][dy]])
{
dis[dx][dy][a[dx][dy]] = dis[tmp.x][tmp.y][tmp.col] + 1;
if (!vis[dx][dy][a[dx][dy]][1])
{
que[++tail] = (point){dx, dy, a[dx][dy], 1};
vis[dx][dy][a[dx][dy]][1] = 1;
}
}
}
}
}
}
if (dis[n][n][0] == 0x3f3f3f3f && dis[n][n][1] == 0x3f3f3f3f) //兩種顏色都無法走到
printf("-1\n");
else
printf("%d\n", min(dis[n][n][0], dis[n][n][1]));
return 0;
}T4 jump 題面
(認真,認真,認真看!!!)


不愧是T4,難度也是普及蒟蒻所不能及的。
這一題要解決的就兩個問題:
1.如何求最小的g。
2.如何在d,g給定的情況下,求出能得到的最大分數。
問題1是很容易想到的,g必然是在
mi是最小跳躍距離,mx是最大跳躍距離。樸素的DP是
#include <cstdio>
#include <cstring>
const int N = 500007;
int dis[N], num[N], f[N], que[N];
int n, d, k, l, r, ans = 0;
int check(int val)
{
memset(f, -127, sizeof(f)); //因為分數有負數,所以賦為負無窮大
int head = 1, tail = 0, mi = val < d ? d - val : 1, mx = d + val, ret = 0, fir = -1;
que[++tail] = 0, f[0] = 0; //初始化
for (int i = 1; i <= n; i++)
{
if (dis[i] < mi) continue; //< mi的點肯定跳不到
if (dis[i] >= mi && fir == -1) //第一個點初始化
fir = i;
if (dis[i] - dis[i - 1] > mx) break; //相鄰兩個已經 > mx了,那麼後面的肯定也都不行
while (dis[i] - dis[fir] >= mi && fir < i) //當fir滿足x[fir]+mi<=x[i]時入隊
{
while (head <= tail && f[fir] > f[que[tail]]) tail--; //入隊
que[++tail] = fir++; //入隊
}
while (head <= tail && dis[que[head]] + mx < dis[i]) head++; //不滿足x[que[head]] + mx >= x[i]的都出隊
if (head > tail) //對於點i,沒有一個點可以跳到
f[i] = -0x7f7f7f7f; //設為賦無窮大
else
f[i] = f[que[head]] + num[i]; //轉移
if (f[i] > ret) //更新最大分數
ret = f[i];
}
return ret >= k; //能夠拿到>= k的分數
}
int main()
{
scanf("%d%d%d", &n, &d, &k);
for (int i = 1; i <= n; i++)
scanf("%d%d", dis + i, num + i);
l = 0, r = dis[n];
while (l <= r) //二分答案
{
int mid = (l + r) >> 1;
if (check(mid)) //答案可行
r = mid - 1, ans = mid/*記錄答案*/;
else
l = mid + 1;
}
if (check(ans)) //保險判斷一下
printf("%d\n", ans);
else
printf("-1\n");
return 0;
}這次普及組的T1意外的水,T4卻意外的難,而且出乎意料的沒有數學題或者思維題,只要是提高-水平的選手一般都能想到3、4題正解,大愛CCF。