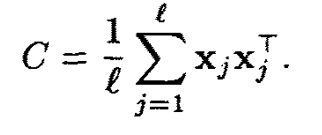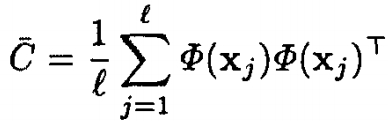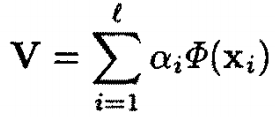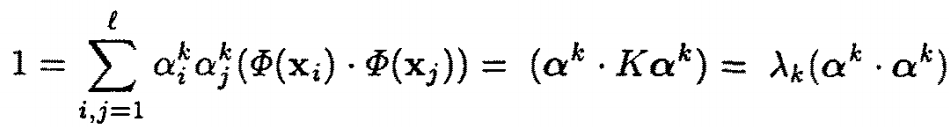1.PCA簡介

    遭遇維度危機的時候，進行特徵選擇有兩種方法，即特徵選擇和特徵抽取。特徵選擇即經過某種法則直接扔掉某些特徵，特徵抽取即利用對映的方法，將高維度的樣本對映至低維度。PCA(或者K-L變換)，即Principal Component Analysis是特徵抽取的主要方法之一。

    PCA適用於非監督的學習的不帶標籤(帶標籤的樣本，往往用LDA降維)的樣本降維，特別是小樣本問題。廣義認為，這類樣本屬性之間的相關性很大，通過對映，將高維樣本向量對映成屬性不相關的樣本向量。PCA的步驟是：
       1.特徵中心化。即每一維的資料都減去該維的均值。
       2.計算協方差矩陣.
       3.計算協方差矩陣的特徵值和特徵向量。
       4.選取從大到小依次選取若干個的特徵值對應的特徵向量，對映得到新的樣本集。
 

         實際上，大的特徵值表徵這個映射向量——或者對映方向，能夠使得樣本在對映後，具有最大的方差。樣本在這個方向最發散（stretched out）通常情況下，有用資訊具有較大的方差，或者說較大的能量。反而言之，小的特徵值對應的特徵向量方向，樣本對映後方差較小，也就是說噪聲往往方差小(如高斯白噪聲)。這是基於通常的情況，當然也可能說，高頻訊號往往類似於噪音(比如說影象噪聲和邊緣)，也有小方差現象，此時可以利用到獨立成分分析(Independent Component Analysis)。

   可以證明，PCA對映過程滿足一定最優性：
 1.重建誤差最小理論(reconstruction error)。誤差的2範數等於未使用(剩下)的映射向量對應的協方差特徵值之和。
        2.最大方差理論
 
。在訊號處理中認為訊號具有較大的方差，噪聲有較小的方差，信噪比(訊號與噪聲的方差比）越大越好。
        3.最小平方誤差理論。簡單理解，利用2範數求導可以得到樣本中心最能代表所有的樣本點，倘若從樣本中心畫出一條直線，在高維空間擬合樣本集(即所有的樣本離這條直線的垂直距離之和最短)。求出來的直線的方向，也是映射向量的方向，且大特徵向量對應的方向所得到的直線，該平方誤差最小。

2.Kernel-PCA

   可以認為，PCA是一個去屬性相關性的過程，這裡的相關性主要指的是線性相關性，那麼對於非線性的情況，怎麼辦，那這就涉及到Kernel—PCA即所謂的核PCA(KPCA)。直觀來說，核PCA就是將原樣本通過核對映後，在核空間基礎上做PCA降維。自然而然，考慮用於分解的協方差矩陣，也應該變化。

     PCA的協方差矩陣為

     KPCA的協方差矩陣為

       l為樣本總數。我們先假設樣本在核對映Φ(x)後也是中心化的——樣本集經過Φ(x)一一對映後，均值仍然為0，即

       但是，存在這樣的一個問題，核函式是定義2個向量之間的關係，即 K(x,y)=(Φ(x)•Φ(y))=Φ(x)'Φ(y)，結果是一個值。換句話說，我們不顯式的知道Φ(x)的具體對映機制。那麼這個對映後的協方差矩陣C當然無法顯式計算。

     等等，我們忽略了問題的實質，我們是希望獲得經過對映後降維的樣本向量，只要我們希望得到這個向量，怎麼獲得的，我們並不關心。KPCA的精髓就在於間接得到降維度後樣本向量。

     我們先定義向量內積(X•Y)=X'*Y。

     假設我們已經得到KPCA協方差C，和它分解後的得到的某個映射向量v，對應特徵值為λ。對於任意一個在核空間表徵的樣本Φ(Xk)。一定存在：

公式1：    

     考慮到。對於PCA的這個過程，可以理解為——希望得到一組基向量，用這組基向量最大可能的線性表徵原來的樣本，基向量的個數即是被降維後的樣本維度，原來樣本與某個基向量的內積即是這種線性表徵的加權係數。所有內積組合成向量，就是降維後的樣本向量。

     那麼，經過矩陣變換，任意一個映射向量V，也可以由所有訓練樣本線性表徵。即：

公式2: 

     定義l*l維的矩陣K的第(i,j)元素為：

公式3 

     將所有對映後的樣本將寫成矩陣，帶入公式1。利用公式2和公式3，可以的求出：

公式4 

     現在顯式求映射向量V的問題就轉換成求係數向量α的問題了。知道了α，我們就可以利用公式2加權所有的樣本集求出映射向量V。

     當然，求解公式4得到α等同於求解下列公式，這也是矩陣分解的問題。α實際為下列等式的特徵向量：

     至此，我們知道，Kernel-PCA真正需要分解的即是矩陣K，加權係數向量α為K的特徵向量。

     考慮到的映射向量V為單位向量，對於第k個映射向量Vk，利用公式2，有：

     αk和λk分別是矩陣K分解後對應的第k個特徵向量和特徵值。此時K的特徵向量或者V的加權係數向量αk，要在單位矩陣的基礎上進一步歸一化(除以根號下λk)。

      總結：KPCA的步驟：

          1.利用核方程K(x,y)計算矩陣K。
         2.PCA分解矩陣矩陣K，獲得前M個單位化映射向量V
         3.對於每個α，對它再次除以對應的特徵值λ的開方，進行再次"歸一化"
         4.對於新的樣本x，分別在1-M個映射向量上對映(作內積)，第k(1<=k<=M)個對映結果等於：

3.Kernel-PCA的對映樣本中心化問題

     實際上，我們是很難滿足最初的假設——對映後樣本仍舊中心化這一前提，即

     現在考慮樣本集對映後非歸一化，我們令第i個樣本集的對映結果簡化形式：

代表

    重新定義實際目標分解矩陣K，假設現在的樣本集長度為N。則對樣本在核對映空間中心化後求得的目標分解矩陣K的第(i,j)個元素為:

    同理，仍然可以轉換到不顯式知道Φ(x)的對映機制，間接求得對映後樣本特徵向量的目的。

4.常見的核函式和多項式核顯式對映機制

    常見的核函式如下：

    我們這裡分析多項式核的基本模式：

    對於上面描敘多項式核，可以化簡為上面基本模式（將a乘入x,將c開根號，分別新增為x,y的一項）

    考慮x,y均為2維的情況，當d=2時，實際是在計算

    可以看出，多項式核的Φ(x)對映機制，是將其對映至了3維空間(儘管上式寫作4維，但x1x2==x2x1，故有意義的只有3維)。

    實際上，倘若樣本x為p維，多項式核的對映結果實際上是----多項式(x1+x2+...........xp).^d完全分解合併後剩下的項，去掉加號這些項(包括係數)構成的向量，即是對映後的結果。

    如上(x1+x2).^2對映成了3維空間。總結而言，p維特徵向量，在多項式的Φ(x)對映後維度表示為排列組合是C(d,d+p-1)。

    當然，若x仍舊為p維，且多項式核為以下形式：

    對應Φ(x)對映後維度表示為排列組合是C(d,d+p)。因為c可以開根號分別新增為x,y的一項。

    到此，核PCA講完了。

    對於Kernel-PCA。是不是可以這樣認為:傳統的PCA去掉了屬性之間的線性相關性；而KPCA關注於樣本的非線性相關：它隱式地將樣本對映至高維(相對於原樣本維度)後屬性之間又變為線性相關，即KPCA的實質：
1.用高維樣本屬性(核對映)的線性相關儘量(擬合，有損)表徵了低維樣本屬性的非線性相關
      2.間接使用PCA去掉了高維屬性的線性相關

      高斯核 K(x1, x2) = exp(−∥x1 − x2∥2/2σ2)，這個核就是最開始提到過的會將原始空間對映為無窮維空間的那個傢伙。不過，如果 σ 選得很大的話，高次特徵上的權重實際上衰減得非常快，所以實際上（數值上近似一下）相當於一個低維的子空間；反過來，如果 σ 選得很小，則可以將任意的資料對映為線性可分——當然，這並不一定是好事，因為隨之而來的可能是非常嚴重的過擬合問題。不過，總的來說，通過調控引數 σ，高斯核實際上具有相當高的靈活性，也是使用最廣泛的核函式之一。

    一句話總結KPCA：間接使用核對映去掉原樣本屬性之間非線性相關性，使用PCA和核函式間接達到降維的目的。

我整理了一些PCA和KPCA的精煉文件5篇，點選下載《PCA和KPCA》

參考：