《機器學習實戰》筆記之十——利用K均值聚類演算法對未標註資料分組
第十章 利用K均值聚類演算法對未標註資料分組
10.1 K-均值聚類演算法
K-均值是發現給定資料集的k個簇的演算法,每個簇通過其質心來描述。其優點為容易實現,但可能收斂到區域性最小值,在大規模資料集上收斂較慢。
隨機確定k個初始點為質心,為每個點找距其最近的質心,並將其分配給該質心所對應的簇,每個簇的質心更新為該簇所有點的平均值。質心可用任意距離度量方式,但結果相應的受到距離度量方式影響。虛擬碼:
coding:
#!/usr/bin/env python # coding=utf-8 from numpy import * def loadDataSet(fileName): #匯入資料集 dataMat = [] fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split("\t") fltLine = map(float,curLine) dataMat.append(fltLine) return dataMat def distEclud(vecA, vecB): #歐式距離 return sqrt(sum(power(vecA - vecB, 2))) def randCent(dataSet, k): n = shape(dataSet)[1] #取dataSet的列數 centroids = mat(zeros((k,n))) #每維都建立k個隨機數,數在每維最大最小值之間 for j in range(n): minJ = min(dataSet[:,j]) #每維最小值 rangeJ = float(max(dataSet[:,j]) - minJ) centroids[:,j] = minJ + rangeJ*random.rand(k,1) #random.rand(k,1),k個0到1.0之間的隨機數 return centroids datMat = mat(loadDataSet("testSet.txt")) #print distEclud(datMat[0],datMat[1]) def kMeans(dataSet, k, distMeas = distEclud, createCent = randCent): m = shape(dataSet)[0] #取資料的行數 clusterAssment = mat(zeros((m,2))) #建立m*2的矩陣,第一列存簇索引值,第二列存誤差 centroids = createCent(dataSet, k) clusterChanged = True while clusterChanged: clusterChanged = False for i in range(m): #對每個資料點來說, minDist = inf minIndex = -1 for j in range(k): #對每維的k個質心,哪個資料點距其最近 distJI = distMeas(centroids[j, :], dataSet[i, :])#距離度量計算質心與資料點之間的距離 if distJI < minDist: #尋找最近質心 minDist = distJI minIndex = j #每個資料點距哪個質心j近,則將其歸到j這個質心 if clusterAssment[i,0] != minIndex: #若資料點i的質心是minIndex這個質心,或者說其質心不變的時候,退出迴圈 clusterChanged = True clusterAssment[i,:] = minIndex, minDist**2 print centroids #打印出每次質心的變化過程 for cent in range(k): ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#將所有歸為cent這個質心的資料點都提出來,計算均值,更新質心的位置。 centroids[cent,:] = mean(ptsInClust, axis = 0) return centroids, clusterAssment datMat = mat(loadDataSet("testSet.txt")) myCentroids, clustAssing = kMeans(datMat, 4)效果:
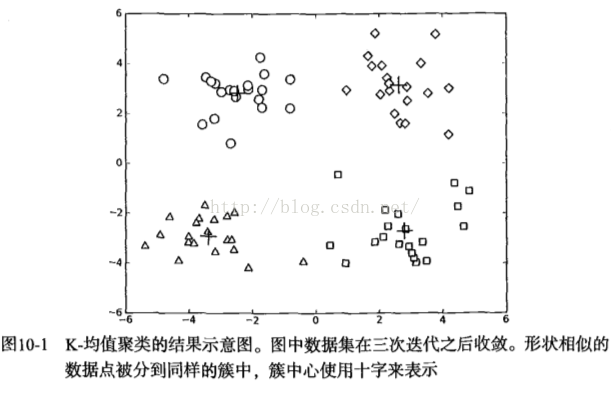

 Figure 10-1: kmeans聚類效果
Figure 10-1: kmeans聚類效果
分析:
從上圖可以看出,選定4個簇進行迭代。迭代次數不是確定的,左邊10次,右邊4次,因為初始質心由隨機數生成,迭代次數跟初始質點的選定還是有很大區別的。
10.2 使用後處理來提高聚類效能
K-均值的缺點是需要預先確定簇的數目k,如何確定k的選擇是否正確是比較重要的問題。K-均值演算法收斂但聚類效果較差的原因是K-均值演算法收斂到了區域性最小值而非全域性最小值。
一種度量聚類效果的指標是SSE(sum of squared error,誤差平方和)。SSE值越小表示資料點越接近於它們的質心,聚類效果也越好。可通過增加簇的個數降低SSE,但不符合聚類的目標:保持簇數目不變的情況下提高簇的質量。可以對生成的簇進行後處理,將具有最大SSE值的簇劃分成兩個簇。將最大簇包含的點過濾出來並在這些點上執行k-均值演算法。也可以將兩個簇進行合併。
10.3 二分K-均值演算法
二分K-均值演算法能克服K-均值演算法收斂於區域性最小值的問題。首先將所有點作為一個簇,然後將該簇一分為二,選擇其中一個簇繼續劃分,選擇哪個取決於對其劃分是否可以最大程度降低SSE的值,不斷劃分,直到使用者指定的簇數目為止。
虛擬碼:
將所有點看成一個簇
當簇數目小於k時,對於每一個簇
選擇使得誤差最小的那個簇進行劃分操作計算總誤差
在給定的簇上面進行K-均值聚類(k=2)
計算將該簇一分為二之後的總誤差
coding
#============二分K-均值聚類演算法====================== def biKmeans(dataSet, k, distMeas=distEclud): m = shape(dataSet)[0] clusterAssment = mat(zeros((m,2))) centroid0 = mean(dataSet, axis=0).tolist()[0] #計算每維均值,得到質心 centList = [centroid0] #用來保留所有質心 for j in range(m): clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2 while (len(centList) < k): lowestSSE = inf for i in range(len(centList)): ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] #get the data points currently in cluster i centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) sseSplit = sum(splitClustAss[:,1]) #compare the SSE to the currrent minimum sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) print "sseSplit, and notSplit: ",sseSplit,sseNotSplit if (sseSplit + sseNotSplit) < lowestSSE: bestCentToSplit = i bestNewCents = centroidMat bestClustAss = splitClustAss.copy() lowestSSE = sseSplit + sseNotSplit bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit print 'the bestCentToSplit is: ',bestCentToSplit print 'the len of bestClustAss is: ', len(bestClustAss) centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] #replace a centroid with two best centroids centList.append(bestNewCents[1,:].tolist()[0]) clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE return mat(centList), clusterAssment dataMat3 = mat(loadDataSet("testSet2.txt")) centList, myNewAssments = biKmeans(dataMat3,3)
效果
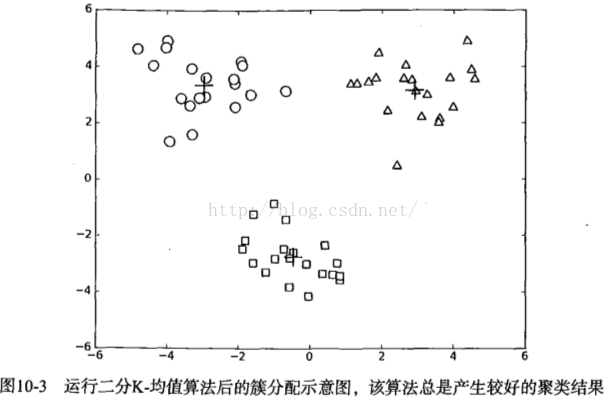
Figure 10-2: 二分k-均值預測結果
10.4 小結
聚類是一種無監督的學習方法。聚類將資料點歸到多個簇中,其中相似資料點處於同一簇中,不相似點處於不同簇中。聚類中可以使用多種不同的方法來計算相似度。
在python scipy包中也實現了一些聚類演算法,from scipy.cluster.vp import *可以找到kmeans2函式,通過內建函式直接計算聚類的質心,可參考部落格http://blog.csdn.net/u010454729/article/details/41158167。