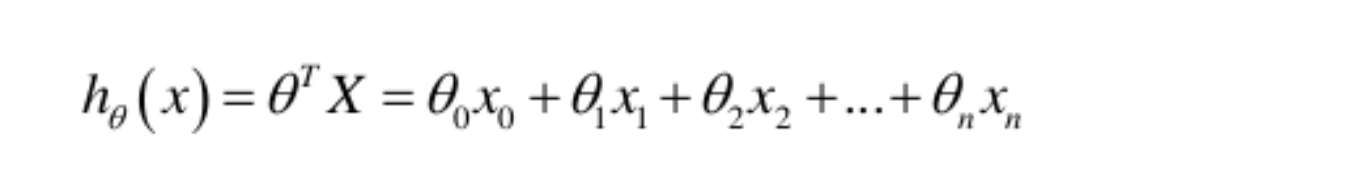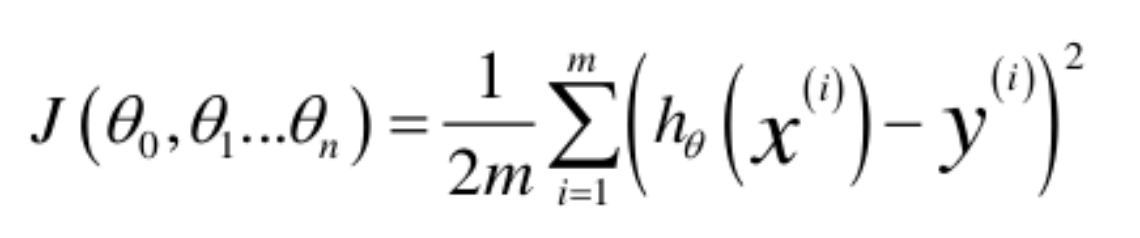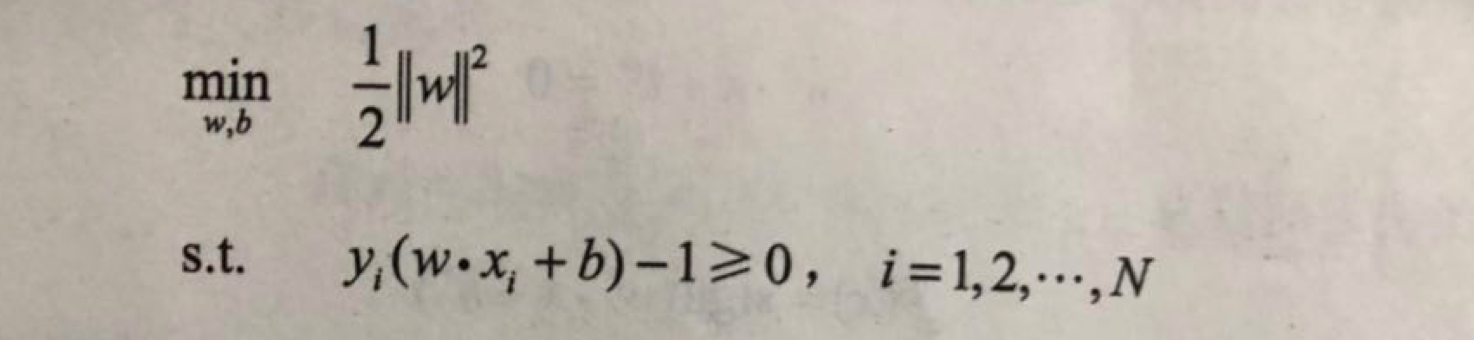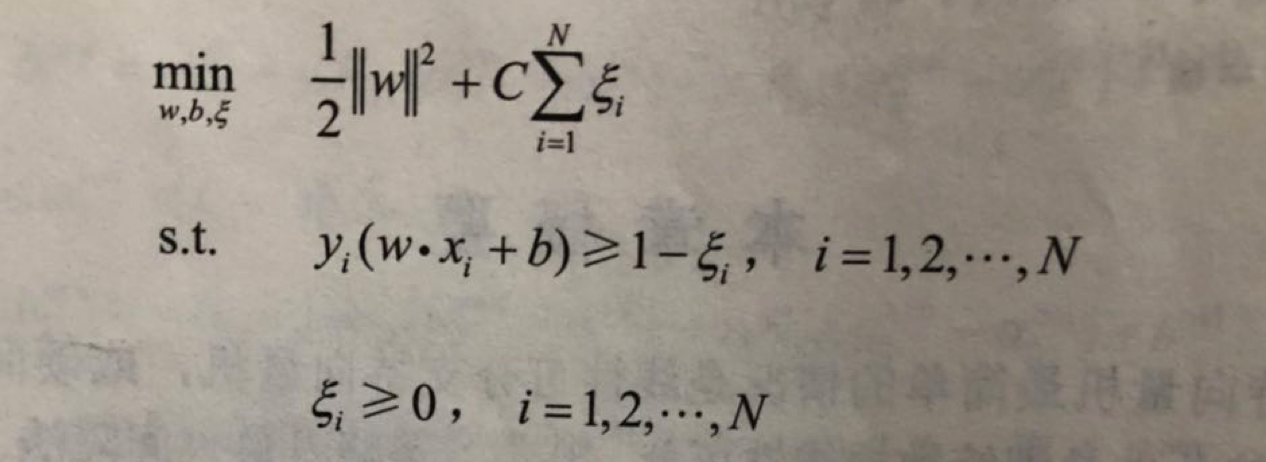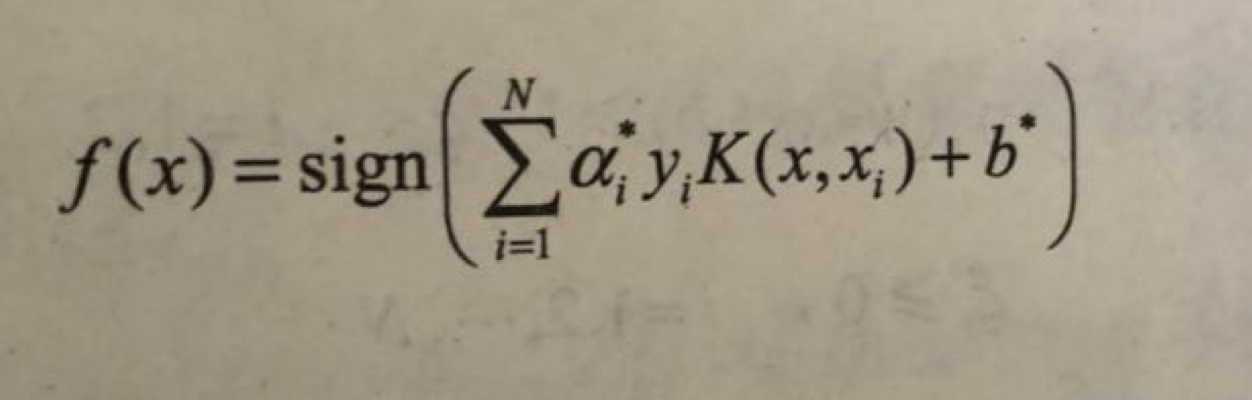一, 線性迴歸(linear regression)

 引入:


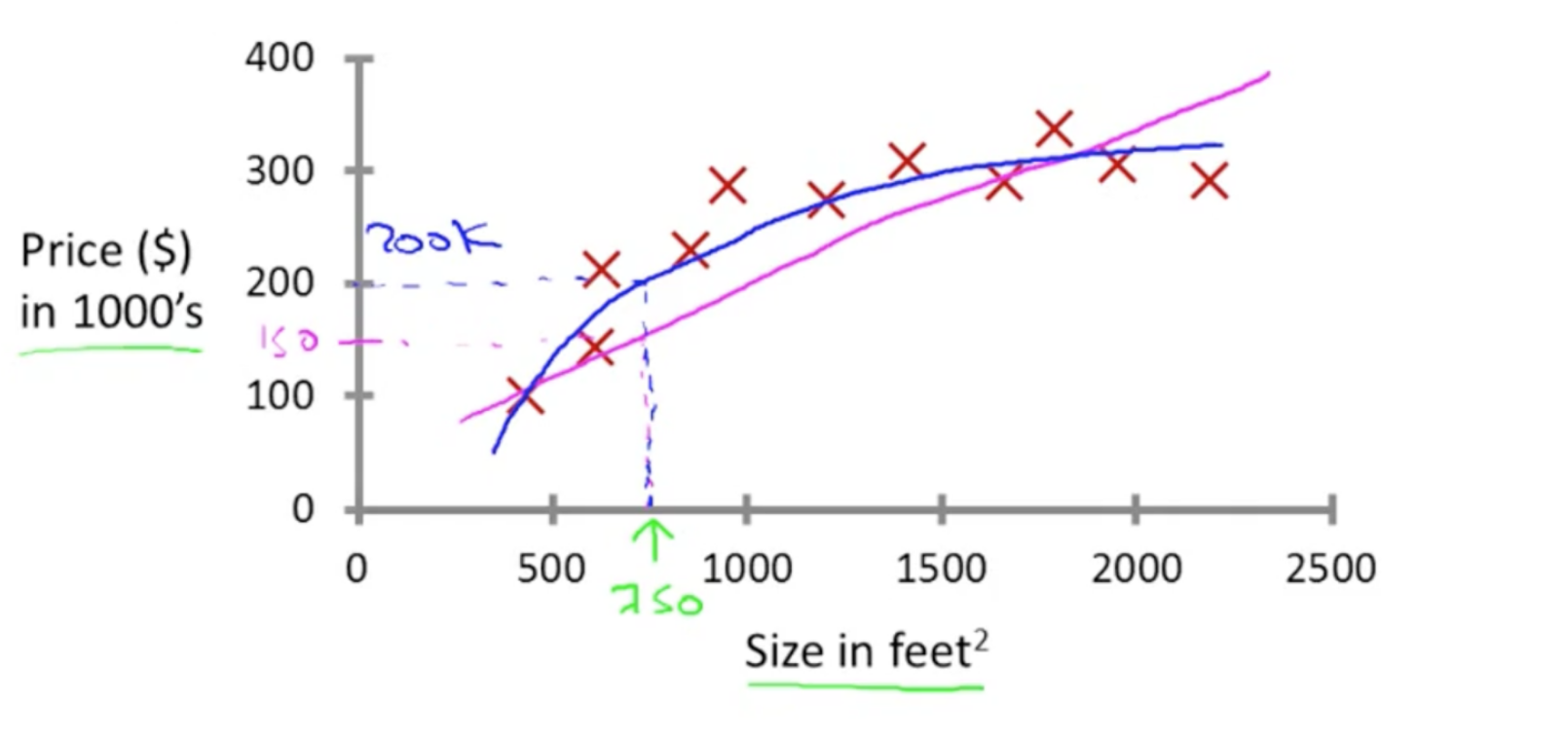
房價預測(以英尺計算)

表示式

 衡量好壞的標準:代價函式

 去往何方?


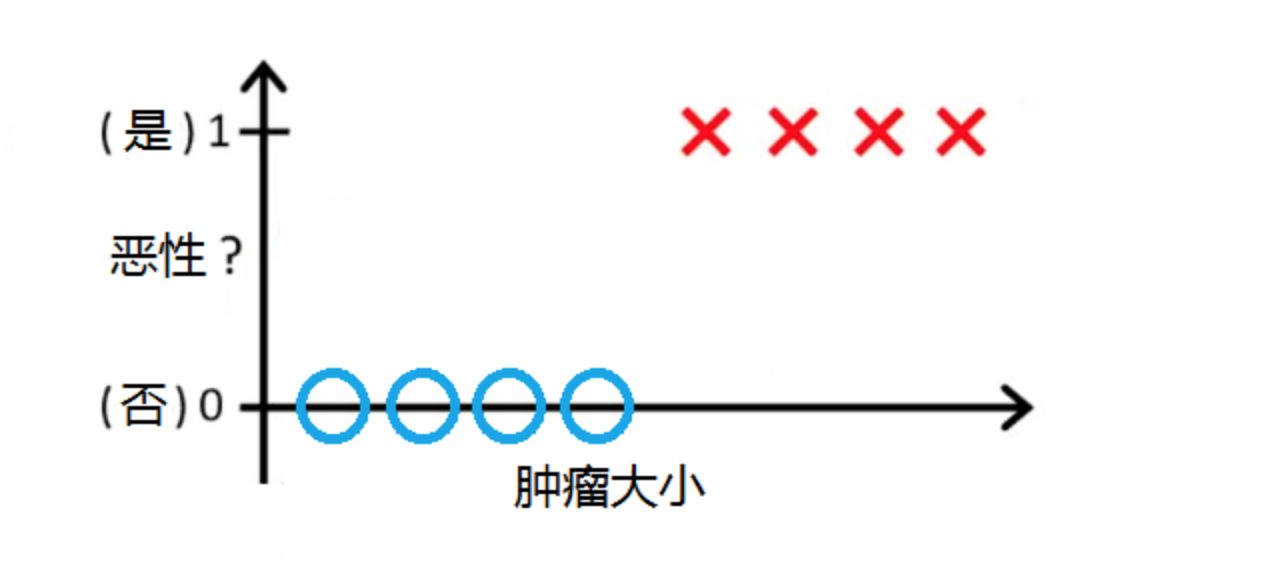
值域目前是無窮大,假如我想解決分類問題,應該如何才能把值域控制在一個較小的區間範圍之內呢?

試想如下案例:

二,邏輯斯蒂迴歸模型(logistics regression)

(logistic regression)是統計學習中經典的分類方法.(屬於對數線性模型)




表示式:

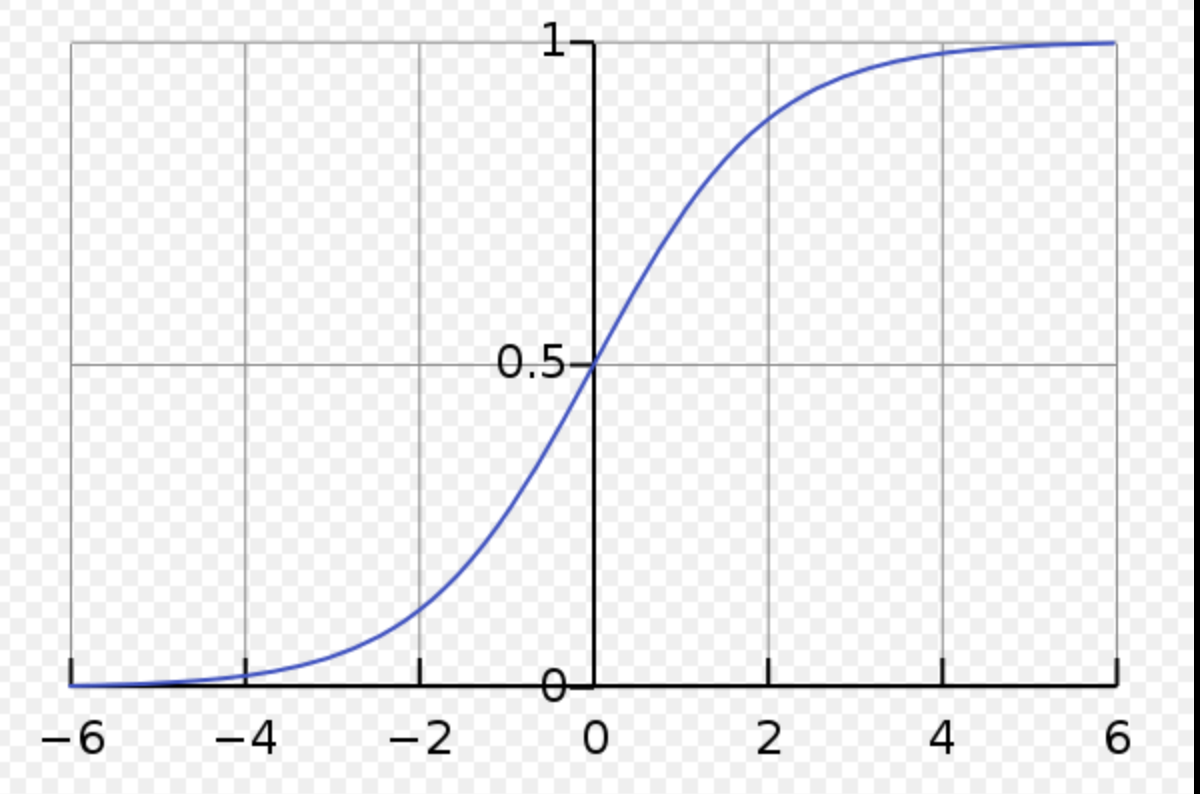
sigmoid:

優點:


1. 是邏輯迴歸的演算法已經比較成熟，預測較為準確；
2. 該模型求出的係數易於理解，便於解釋，不屬於黑盒模型，尤其在銀行業，80%的預測是使用邏輯迴歸；
3. 其結果是概率值，可以做ranking model；
4. 訓練比較快;


缺點:


1. 分類較多的y都不是很適用；
2. 對於自變數的多重共線性比較敏感，所以需要利用因子分析或聚類分析來選擇代表性的自變數；
3. 其預測結果呈現S型，兩端概率變化小，中間概率變化大比較敏感，導致很多區間的變數的變化對目標概率的影響沒有區分度，無法確定閾值;






應用:廣告行業的點選率預估:LR作為CTR預估的一個經典模型


把被點選的樣本當成正例，把未點選的樣本當成負例，那麼樣本的ctr實際上就是樣本為正例的概率，LR可以輸出樣本為正例的概率，所以可以用來解決這類問題




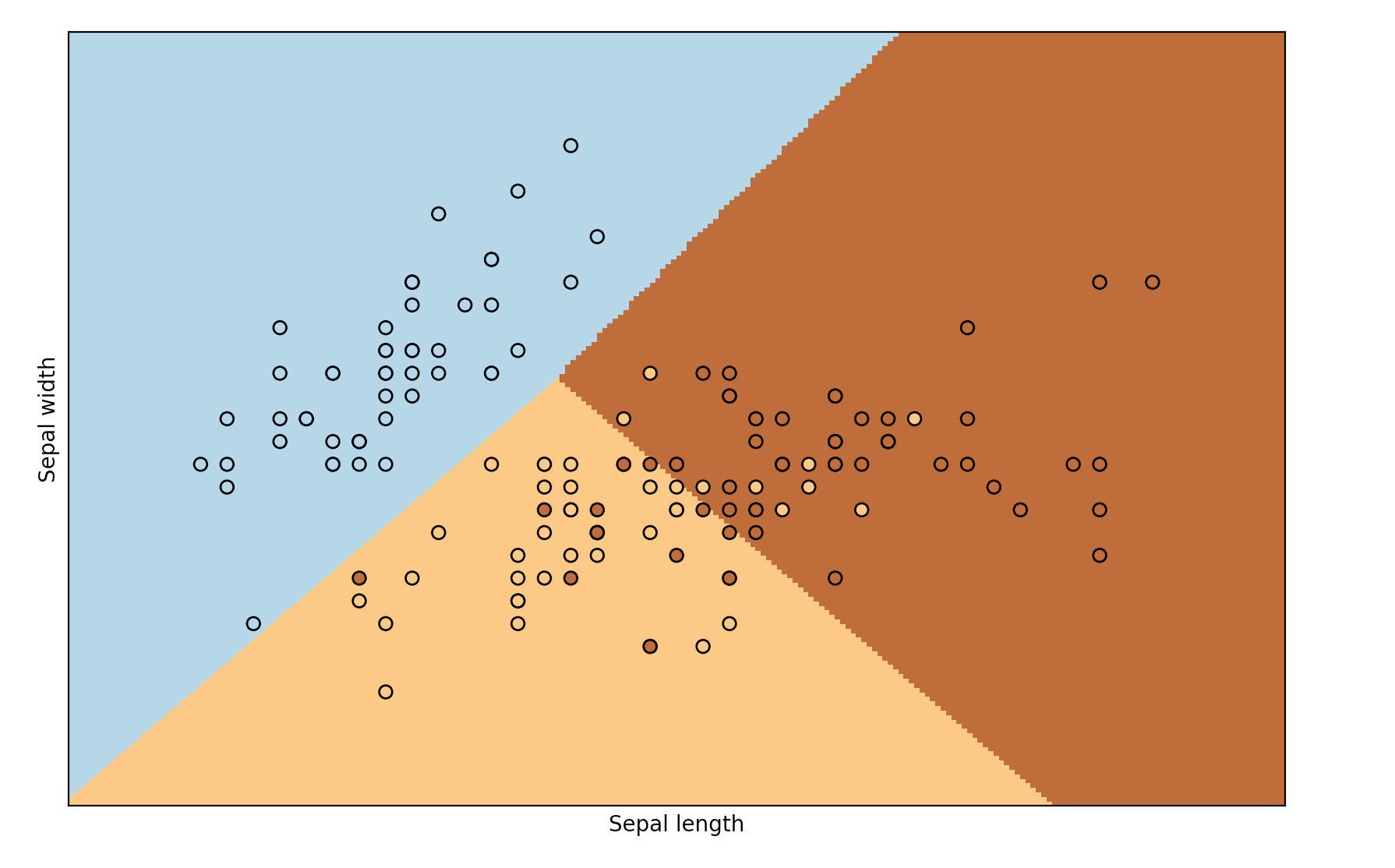
實戰例子:


plot_iris_logistic.py

三,支援向量機.

它是一種二分類模型,它的基本模型是定義在特徵空間上的間隔最大的線性分類器,SVM的學習策略就是間隔最大化,可形式化為一個求解凸二次規劃的問題,也定價於正則化的合頁損失函式的最小化問題,SVM的學習演算法是求解凸二次規劃的最優化演算法.

I,線性可分支援向量機(或硬間隔支援向量機)

構造它的條件是:訓練資料線性可分,其學習策略是最大間隔法,可表示為凸二次規劃問題,其原始最優化問題是:

求得最優化問題的解為w,b,得到線性可分支援向量機,分離超平面是:


w*x+b=0


分類決策函式是:


f(x)=sign(w*x+b)


線性可分支援向量機的最優解存在且唯一,位於間隔邊界上的例項點為支援向量,最優分離超平面由支援向量完全決定.


二次規劃問題的對偶問題是:








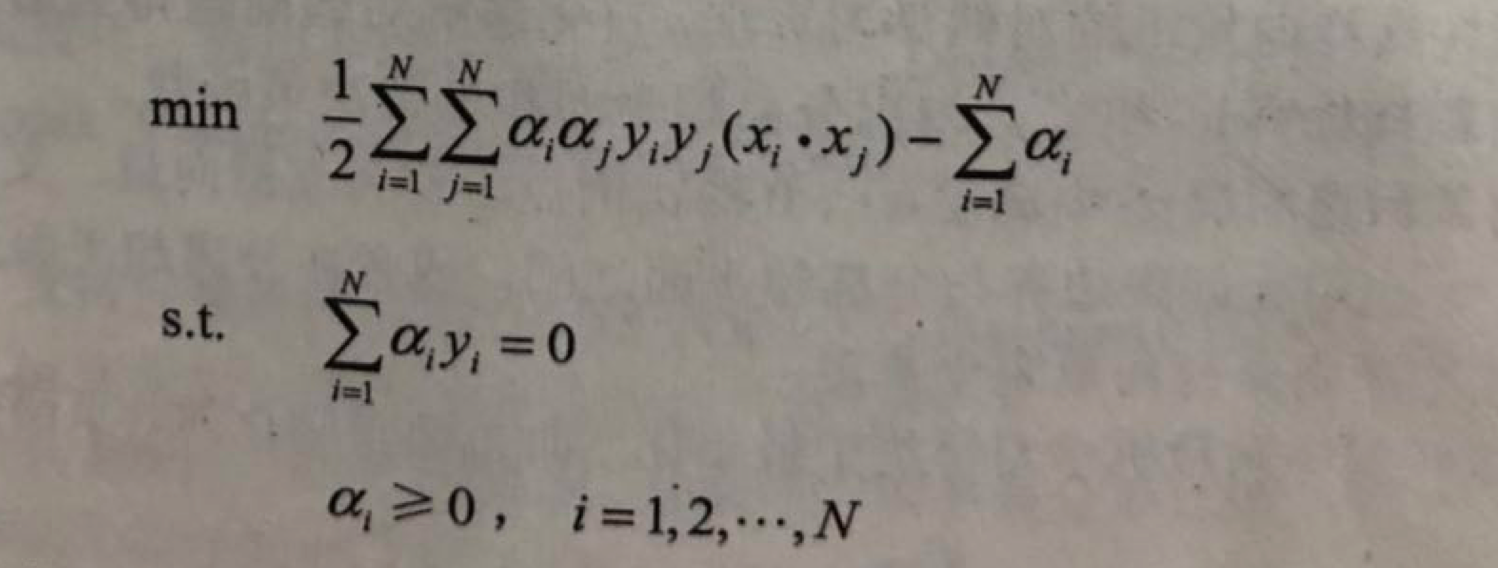
通常,通過求解對偶問題學習線性可分支援向量機,即首先求解對偶問題的最優值a,然後求最優值w和b,得出分離超平面和分類決策函式.

II,線性支援向量機(或軟間隔支援向量機)

ps:現實中訓練資料是線性可分的情形較少,訓練資料往往是近似線性可分的.

對於噪聲或者例外,通過引入鬆弛變數ζ,使其"可分",得到線性支援向量機學習的凸二次規劃問題,其原始最優化問題是:

求解原始最優化問題的解 w,b,得到線性支援向量機,其分離超平面為:


w*x+b=0


分類決策函式為:f(x)=sign(w*x+b)


線性支援向量機的解w唯一但 b 不一定唯一.
其對偶問題是:

線性支援向量機的對偶學習演算法.首先求解對偶問題得到最優解a,然後求原始問題最優解w,b,得出分離超平面和分類決策函式.


線性支援向量機學習等價於最小化二階範數正則化的合頁函式.

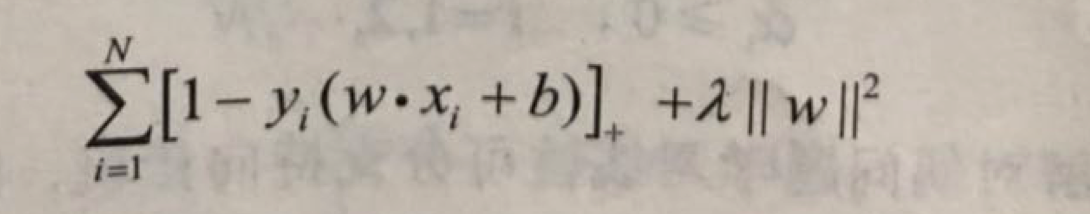
 III,非線性支援向量機

對於輸入空間中的非線性分類問題,可以通過非線性變換將它轉化為某個高維特徵空間中的線性分類問題.在高維特徵空間學習線性支援向量機.由於線上性支援向量機學習的對偶問題裡,目標函式和分類決策函式都只涉及例項與例項之間的內積,所以不需要顯示的指定非線性變換,而是用核函式來替換當中的內積,核函式表示,通過一個非線性轉換後的兩個例項間的內積.具體的,k(x,z)是一個核函式或正定核,意味著存在一個從輸入空間x到特徵空間h的對映Φ(x):x->h,對於任意x,z∈ x,有


k(x,z)=Φ(x)*Φ(z)


對稱函式k(x,z)為正定核的充要條件如下:對任意xi∈ X,i=1,2,...,m ,任意正整數m,對稱函式k(x,z)對應的Gram矩陣是半正定的.
所以,線上性支援向量機學習的對偶問題中,用核函式k(x,z)替代內積,求解得到的就是非線性支援向量機