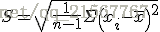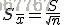標準差

標準差（又稱標準偏差、均方差，英語：Standard Deviation，縮寫SD），數學符號σ（sigma），在概率統計中最常使用作為測量一組數值的離散程度之用。

標準差定義：

為方差開算術平方根，反映組內個體間的離散程度；標準差與期望值之比為標準離差率。測量到分佈程度的結果，原則上具有兩種性質：

1、為非負數值（因為開平方後再做平方根）；
2、與測量資料具有相同單位（這樣才能比對）。

計算公式

標準誤

標準誤差（英文：Standard Error），也稱標準誤，即樣本統計量的標準差（英文：Standard Deviation），是描述對應的樣本統計量抽樣分佈的離散程度及衡量對應樣本統計量抽樣誤差大小的尺度。

如果已知資料來源的標準差(σ)，那麼抽取無限多份大小為 n 的樣本，每個樣本各有一個平均值，所有這個大小的樣本之平均值的標準差可證明為：

Sx¯=σn√$S_{\overline{x}}=\frac{\sigma }{\sqrt{n}}$

但由於通常σ為未知，此時可以用研究中取得樣本的標準差 (s) 來估計 SDx¯${\displaystyle S{D}_{\overline{x}}}$

CV值

在概率論和統計學中，變異係數，又稱“離散係數”（英文：coefficient of variation），是概率分佈離散程度的一個歸一化量度，其定義為標準差 σ$\sigma$ 與平均值 μ$\mu$ 之比:

Cv=σμ$Cv=\frac{\sigma }{\mu }$

變異係數（coefficient of variation）只在平均值不為零時有定義，而且一般適用於平均值大於零的情況。變異係數也被稱為標準離差率或單位風險。

變異係數只對由比率標量計算出來的數值有意義。舉例來說，對於一個氣溫的分佈，使用開爾文或攝氏度來計算的話並不會改變標準差的值，但是溫度的平均值會改變，因此使用不同的溫標的話得出的變異係數是不同的。也就是說，使用區間標量得到的變異係數是沒有意義的。