\(\color{#0066ff}{ 題目描述 }\)

你有一支由 \(n\) 名預備役士兵組成的部隊，士兵從 \(1\) 到 \(n\) 編號，要將他們拆分 成若干特別行動隊調入戰場。出於默契的考慮，同一支特別行動隊中隊員的編號 應該連續，即為形如\((i, i + 1, ..., i + k)\)的序列。 編號為 i 的士兵的初始戰鬥力為 xi ，一支特別行動隊的初始戰鬥力 x 為隊內 士兵初始戰鬥力之和，即 \(x = x_i + x_{i+1} + ... + x_{i+k}\)

通過長期的觀察，你總結出一支特別行動隊的初始戰鬥力 \(x\) 將按如下經驗公 式修正為 \(x':x'= ax^2+bx+c\)

例如，你有 4 名士兵， \(x_1 = 2, x_2 = 2, x_3 = 3, x_4 = 4\)。經驗公式中的引數為 \(a = –1, b = 10, c = –20\)。此時，最佳方案是將士兵組成 \(3\) 個特別行動隊：第一隊包含士兵 \(1\) 和士兵 \(2\)，第二隊包含士兵 \(3\)，第三隊包含士兵 \(4\)。特別行動隊的初始戰鬥力分 別為 \(4, 3, 4\)，修正後的戰鬥力分別為 \(4, 1, 4\)

\(\color{#0066ff}{輸入格式}\)

輸入由三行組成。第一行包含一個整數 \(n\)，表示士兵的總數。第二行包含三 個整數 \(a, b, c\)，經驗公式中各項的係數。第三行包含 \(n\) 個用空格分隔的整數 \(x_1, x_2, …, x_n\)，分別表示編號為 \(1, 2, …, n\) 的士兵的初始戰鬥力。

\(\color{#0066ff}{輸出格式}\)

輸出一個整數，表示所有特別行動隊修正後戰鬥力之和的最大值。

\(\color{#0066ff}{輸入樣例}\)

4 
-1 10 -20 
2 2 3 4 
 

\(\color{#0066ff}{輸出樣例}\)

9

\(\color{#0066ff}{資料範圍與提示}\)

20%的資料中，n ≤ 1000；

50%的資料中，n ≤ 10,000；

100%的資料中，1 ≤ n ≤ 1,000,000，–5 ≤ a ≤ –1，|b| ≤ 10,000,000，|c| ≤ 10,000,000，1 ≤ xi ≤ 100

\(\color{#0066ff}{題解}\)

不難得出DP式子

\(f[i]\)代表\(1\to i\)分組的答案， \(s[i]\)代表每個人x的字首和

則\(f[i] = f[j-1] + a*(s[i]-s[j-1])^2+b*(s[i]-s[j-1])+c\)

\(f[i]=f[j-1]+a*s[i]^2+a*s[j-1]^2-2*a*s[i]*s[j-1]+b*s[i]-b*s[j-1]+c\)

\(f[i]=f[j-1]+a*s[j-1]^2-2*a*s[i]*s[j-1]-b*s[j-1]+a*s[i]^2+b*s[i]+c\)

令\(t=a*s[i]^2+b*s[i]+c\)

\(f[i]=f[j-1]+a*s[j-1]^2-(2*a*s[i]+b)*s[j-1]\)

令\(k（斜率）=(2*a*s[i]+b)\)

\(k*s[j-1]+f[i]=f[j-1]+a*s[j-1]^2+t\)

看成平面上的點\((s[j-1],f[j-1]+a*s[j-1]^2)\),t最後加就行了

f[i]作為直線的截距，我們要找最大截距，即維護上凸包

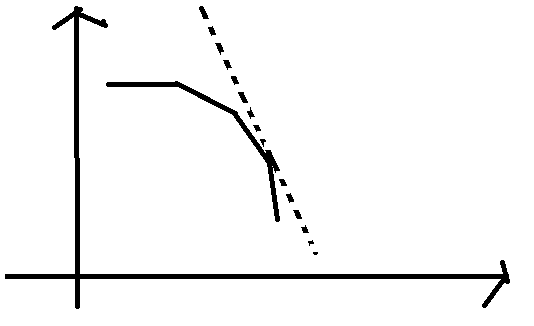
虛線即當前斜率k

則當且僅當k在兩個斜率之間的那個交點處最優

取到最優點後，再維護凸包

可以用雙端佇列

#include<bits/stdc++.h>
#define LL long long
LL in() {
    char ch; int x = 0, f = 1;
    while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
    for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
    return x * f;
}
const int maxn = 1e6 + 100;
const LL inf = 999999999999999LL;
LL f[maxn], s[maxn], a, b, c;
int n;
int head, tail, q[maxn];
LL X(int x) { return s[x]; }
LL Y(int x) { return f[x] + a * s[x] * s[x]; }
double k(int x, int y) { return (double)(Y(x) - Y(y)) / (double)(X(x) - X(y)); }
int main() {
    n = in(), a = in(), b = in(), c = in();
    for(int i = 1; i <= n; i++) s[i] = s[i - 1] + in();
    for(int i = 1; i <= n; i++) {
        LL K = 2LL * a * s[i] + b;
        LL t = a * s[i] * s[i] + b * s[i] + c;
        while(head < tail && K < k(q[head + 1], q[head])) head++;
        f[i] = Y(q[head]) + t - K * X(q[head]);
        while(head < tail && k(q[tail], q[tail - 1]) < k(q[tail], i)) tail--;
        q[++tail] = i;
    }
    printf("%lld\n", f[n]);
    return 0;
}