(二叉樹)二叉樹的最近公共祖先
題目描述
給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。
百度百科中最近公共祖先的定義為:“對於有根樹 T 的兩個結點 p、q,最近公共祖先表示為一個結點 x,滿足 x 是 p、q 的祖先且 x 的深度儘可能大(一個節點也可以是它自己的祖先)。”
例如,給定如下二叉樹: root = [3,5,1,6,2,0,8,null,null,7,4]
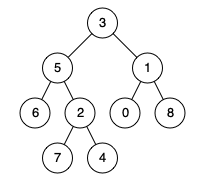
示例 1:
輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出: 3
解釋: 節點 5 和節點 1 的最近公共祖先是節點 3。
示例 2:
輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出: 5
解釋: 節點 5 和節點 4 的最近公共祖先是節點 5。因為根據定義最近公共祖先節點可以為節點本身。
說明:
所有節點的值都是唯一的。
p、q 為不同節點且均存在於給定的二叉樹中。
題目分析
做了一些二叉樹的題,發現二叉樹的查詢問題一般都是從左右子樹遞迴去解決,也往往都能得到答案,因此,這道題可以考慮是否能從左右子樹進行遞迴去解決呢?
首先,要想通過遞迴來實現,就需要先確定臨界條件,那麼臨界條件是什麼呢?換句話說,臨界條件就是遞迴中能夠直接返回的特殊情況,第一點則是最常見的“判空”,判斷根結點是否是空節點,如果是,那麼肯定就可以馬上返回了,這是一個臨界條件;再來考慮題意,在以root為根結點的樹中找到p結點和q結點的最近公共祖先,那麼特殊情況是什麼呢?很顯然,特殊情況就是根結點就等於q結點或p結點的情況,想一下,如果根結點為二者之一,那麼根結點就必定是最近公共祖先了,這時直接返回root即可。由此看來,這道題就一共有三種特殊情況,root == q 、root == p和root==null,這三種情況均直接返回root即可。
根據臨界條件,實際上可以發現這道題已經被簡化為查詢以root為根結點的樹上是否有p結點或者q結點,如果有就返回p結點或q結點,否則返回null。
這樣一來其實就很簡單了,從左右子樹分別進行遞迴,即查詢左右子樹上是否有p結點或者q結點,就一共有4種情況:
第一種情況:左子樹和右子樹均找沒有p結點或者q結點;(這裡特別需要注意,雖然題目上說了p結點和q結點必定都存在,但是遞迴的時候必須把所有情況都考慮進去,因為題目給的條件是針對於整棵樹,而遞迴會到區域性,不一定都滿足整體條件)
第二種情況:左子樹上能找到,但是右子樹上找不到,此時就應當直接返回左子樹的查詢結果;
第三種情況:右子樹上能找到,但是左子樹上找不到,此時就應當直接返回右子樹的查詢結果;
第四種情況:左右子樹上均能找到,說明此時的p結點和q結點分居root結點兩側,此時就應當直接返回root結點了。
綜上也不難寫出結果了:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root==p||root==q||!root)return root; TreeNode* left=lowestCommonAncestor(root->left, p, q); TreeNode* right=lowestCommonAncestor(root->right, p, q); if(!left&&!right)return NULL; else if(left&&!right)return left; else if(right&&!left)return right; return root; }
