ROS中的路徑規劃演算法dijkstra和A*
ROS Navigation包裡面的GlobalPlanner自帶是提供了兩種全域性路徑規劃的方法,dijkstra和A*
dijkstra 大家都知道了,A*在之前的一篇部落格裡面有介紹
A*
評估函式 為 f(n) = g(n) + h(n)
g(n) 為起點到已經搜尋過的節點的代價值
h(n) 為當前節點到目標節點(終點)的值
在這裡我們可以看到A* 考慮了已經遍歷過的點和未遍歷過的點兩個部分綜合起來考慮整體來評估代價值
特別的,當f(n) = g(n)的時候為Dijkstra演算法
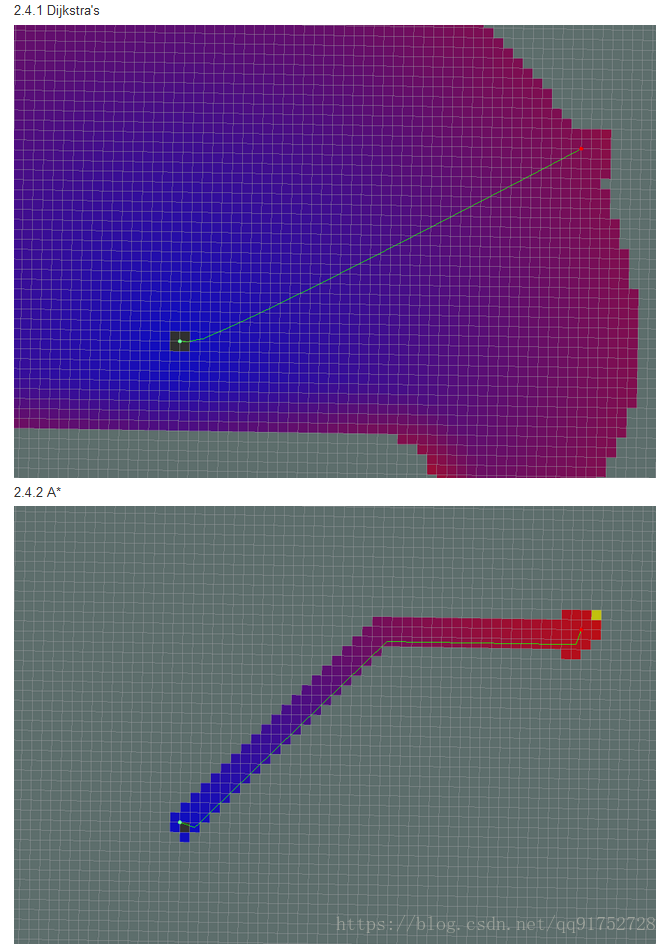
這裡附上ROS的介紹效果圖
這裡還有一個值得注意的點,在ROS自帶Navigation的實現裡面是沒有提供類似D*這樣的動態方法
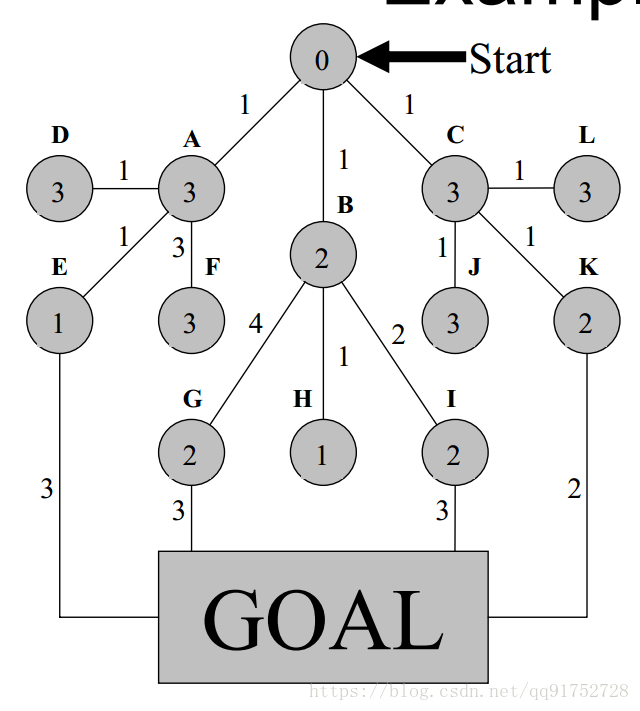
這裡講解一個例子
每個節點內部的灰色部分是它的h(x),注意這裡的h(x)並不是由它到終點的路徑來計算的,可以看作是隨意定義的吧,實際情況上這個h(x)的選取本來就是各有不同的。只是在柵格地圖中我們用的是歐氏距離
1.根據圖中來初始化每個節點的f(x)函式的值
例如
f(B) = 1 + 2 = 3 (Start到B的距離 加上 B的h(x)值也就是中心灰色的值)
f(A) = 1 + 3 = 4
f(C) = 1 + 3 = 4
可得
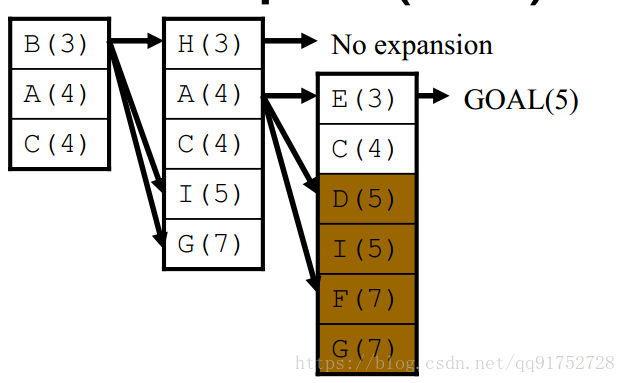
顯然,目前還沒有找到Start到Goal的路徑,所以進行擴充(expand)
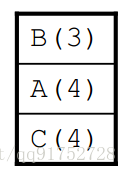
2.從Start的鄰近節點開始擴充
上面圖中的這個擴充應該不難理解。
顯然我們現在得到了一個路徑
Start -> A -> E -> Goal 路徑的代價值為1+1+3 = 5
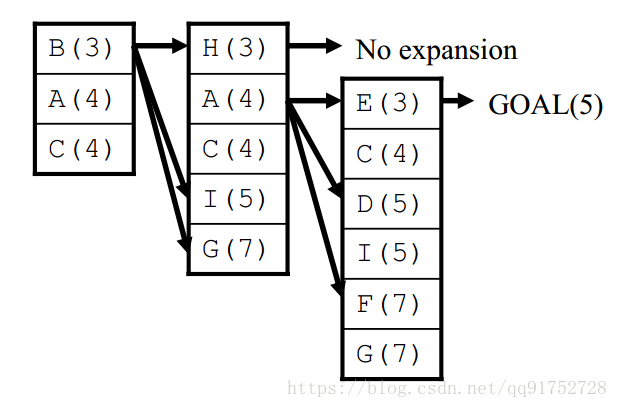
3.但是目前我們不確定有沒有更短的路徑,所以這一步需要先刪除代價值大於5的路徑,然後再進行擴充
這裡D,I,F,G就被移除了,不對它們進行擴充了
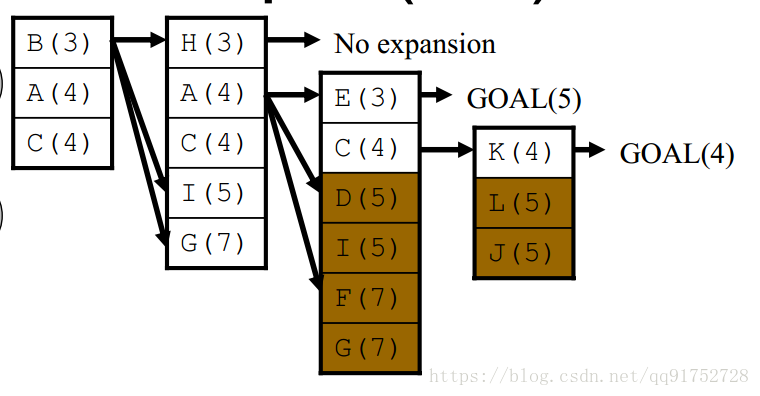
再繼續進行擴充,現在還可以進行擴充的就是節點C了
這裡得到了一條Start -> C -> K -> Goal 的路徑,代價值為4
所以得到的最終路徑為Start -> C -> K -> Goal