https://www.luogu.org/problemnew/show/CF468D

題目大意：

有一個n個節點的樹（編號1~n）。樹上的每一個邊都是正值。

我們定義兩點之間的距離dis(v,u)為這兩點最短路徑邊的權值之和。

設數列p為一個1~n的全排列。求使得sigma dis(i,pi​)最大的、字典序列最小的全排列p。

思路：

我們先選擇任意一個點當做根，然後令dep[i]表示i到根距離。
接下來可以變換一下目標式

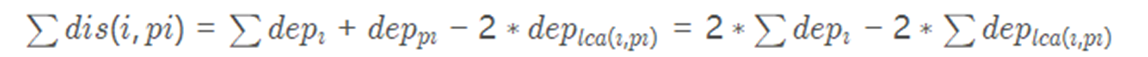
在根確定的情況下，減號前面部分的值是定的，只需要最小化後面部分。
可以給出的結論是，如果我們選擇重心為根，後面部分可以最小為0。
這顯然是答案下界，接下來我們給出構造方案。

以不同點為根，最終答案一樣，我們不妨用重心為根，好算。

重心的性質是，每個子樹的大小都不超過n/2。
結論是，一定存在一個排列p，使得i和p[i]不在一個子樹中。
不妨考慮歸納的證明。
顯然n<=2該結論都成立。
考慮如果n成立，那麼n+2也成立。
找到n+2情況最大的子樹，任取一個葉子，並找到另一個子樹中一個葉子（因為節點數大於2，一定有至少兩個子樹），設為i和j，則令p[i]=j，p[j]=i，然後刪去這兩個葉子。
最大子樹不超過n/2+1，刪去一個葉子後就不超過n/2，顯然我們歸納到了更小情況。

那麼當一個子樹出現t+x=n−i時，就很關鍵了，因為i在不斷變大，因此右邊會減小，如果左邊不能隨之減小，就會不合法。
而可以知道每次一個子樹t和x只可能其中一個減了1，因此這個等式其實就一直滿足了！所以我們用set維護所有子樹的t+x，每次檢視是否存在滿足等式的子樹，設該子樹為p，那麼接下來，如果i’在p子樹內（t會減一），則可以正常做，否則，我們為其尋找的配對j’必須在p子樹內（x會減一）。找配對的話，可以用線段樹維護，同一個子樹內按編號從小到大放入一個序列中，每次指標往後移即可。
至於根是一個棘手的問題，根和任意都能配對，所以根要特殊考慮一下。