離散基礎 (15). 調和級數分析
阿新 • • 發佈:2019-01-06
1. 定義
2. 問題描述
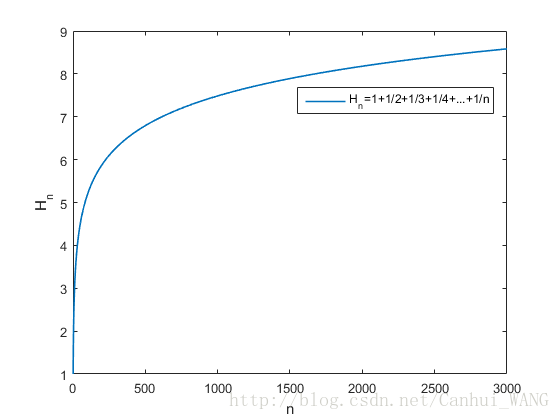
調和級數
3. 問題分析
我們假設紙牌的長度為2,
當1張紙牌時,最大可能的懸空部分的長度為
當2張紙牌時,最大可能的懸空部分的長度為
當3張紙牌時,最大可能的懸空部分的長度為
……
類似地,可以歸納,並證明,
當
5. Matlab演算法實現
harmonic_plot.m
function harmonic_plot(n)
% compute harmonic numbers, where n > 1
t = 1;
for i = 2:n
t = [t, t(i-1)+1/i];
end
% plot
plot(t,'linewidth',1.2);
legend('H_n=1+1/2+1/3+1/4+...+1/n');
xlabel('n');
ylabel('H_n');Terminal
>> harmonic_plot(3000 Results