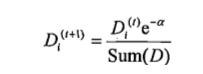期末作業——基於機器學習演算法的LOL比賽預測(求高分,拜託拜託)
前言:2018年5月2日,各大高校男生宿舍不約而同的爆發出尖叫和呼喊聲。難道是“單身少年們”集體受到刺激,而引發的集體抗議嗎?在這一切的背後究竟隱藏著怎樣的祕密?
其實真相是:
一、題目背景
近年來,隨著科技的不斷進步和人們傳統思想的不斷改變,電子競技正在飛速發展。剛剛,亞奧理事會公佈了亞運電子體育表演賽的六個專案:《英雄聯盟》、《實況足球》、《爐石傳說》、《星際爭霸2》、《Arena of Valor》(王者榮耀國際版)和《皇室戰爭》。它們將作為電子競技攜手奧運的排頭兵,出現在八月舉行的雅加達亞運會賽場上。而我本人對英雄聯盟(LOL)這門賽事比較感興趣,於是自選了這個題目。
二、樣本來源
本人選用的樣本資料來源於英雄聯盟官網 http://lpl.qq.com/es/lpl/2018/
三、資料視覺化及資料預處理
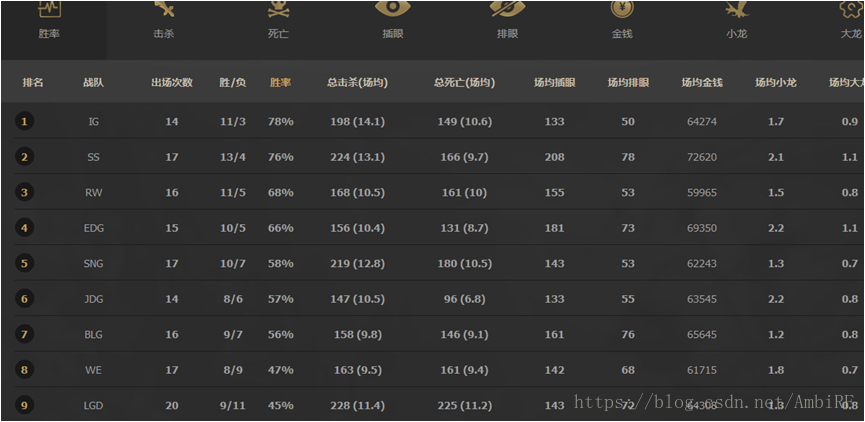
在我們拿到原始資料後,需要對資料進行預處理,提高資料質量,從而提高挖掘結果的質量。通過剛才的網頁資料我們可以發現,其官方網站上所給出的資訊非常多。但實際上我們在預測的過程中並不需要那麼多的資料。

所以選擇合適的特徵就顯得更加重要!
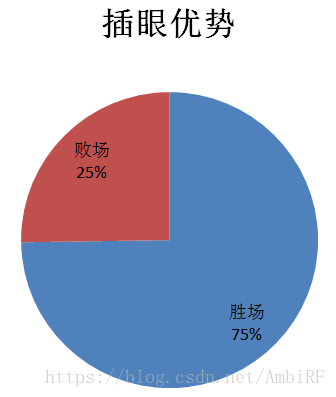
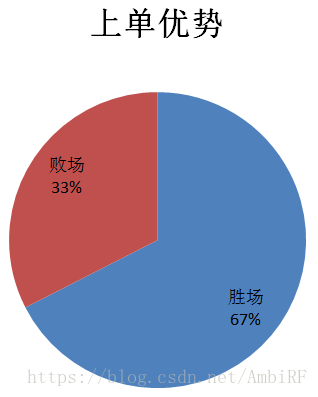
通過做出資料視覺化,來觀察其特徵對最後結果的影響:
由此看見,無論是插眼還是上單對於最後結果的影響都舉足輕重,後邊的資料視覺化我就不一一展示了。當然,除了運用這種直觀的方式觀察和比對特徵值對於最後結果的影響之外,我還採用了經驗法(其實就是問大神)。這種方法的好處就是除了提供的特徵外,我們還可以自己發掘一些隱藏關係,建立新的特徵並驗算新的特徵值對於結果的影響。
最後我選取了隊伍十個特徵,作為預測的基礎。他們分別是:上單差距、中單差距、打野差距、下路差距、協作能力差距、平均小龍數差距、平均大龍數差距、場均插眼差距、場均擊殺差距和場均死亡差距。
首先對特徵做一個簡單的介紹,前四條差距代表了戰隊出戰選手個人能力的差距,我們都知道一個選手的好壞無疑影響著最後的結果,尾大不掉的現象是確確實實存在的。除此之外,協作能力的差距這一個特徵並沒有體現在官方所提供的資料中,因此我自己擬定了一個函式:
這代表著擊殺對方一名選手所需要的己方人手。而場均大龍小龍則代表著隊伍對於地圖公共資源的爭奪意識,場均插眼差距可以反映隊伍對於地圖資訊量的把握,只有時時刻刻掌握敵方動向,才能知己知彼,百戰不殆。
將我們所需要的資料收集後,按照所選定的十個特徵值整理成表格的形式,儲存,作為資料庫。
四、演算法選擇
4.1使用Adaboost演算法預測
4.1.1 boost前提介紹
提升(Boost)簡單地來說,提升就是指每一步我都產生一個弱預測模型,然後加權累加到總模型中,然後每一步弱預測模型生成的的依據都是損失函式的負梯度方向,這樣若干步以後就可以達到逼近損失函式區域性最小值的目標。boosting分類的結果是基於所有分類器的加權求和結果的,分類器每個權重代表的是其對應分類器在上一輪迭代中的成功度。而bagging中的分類器權重是相等的。其中Adaboost就是boosting方法中一個極具代表性的分類器。
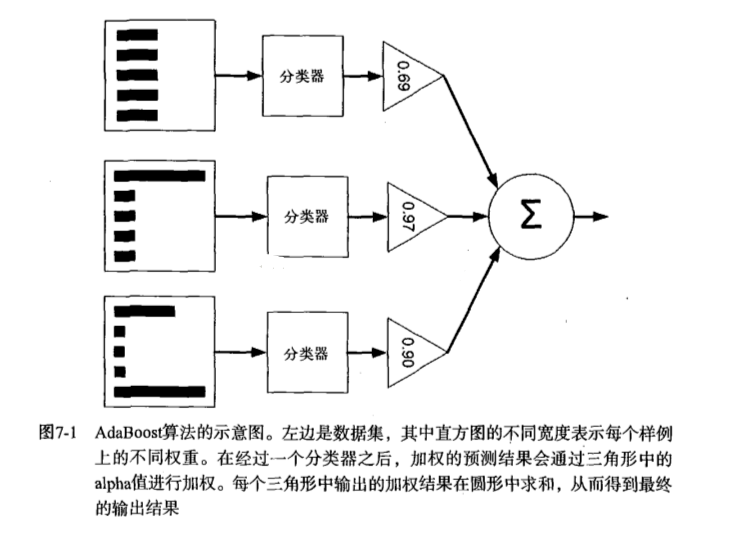
4.1.2 Adaboost訓練演算法介紹
AdaBoost(adaptiveboosting):訓練資料中的每個樣本,並賦予其一個權重,這些權重構成了向量D。一開始,這些權重都初始化成相等值。首先在訓練資料上訓練出一個弱分類器並計算該分類器的錯誤率,然後在同一資料集上再次訓練弱分類器。重新調整每個樣本的權重,第一次分對的樣本的權重將會降低,分錯的樣本的權重將會提高。AdaBoost為每個分類器都分配了一個權重值alpha,其基於每個弱分類器的錯誤率進行計算的。錯誤率的定義:
AdaBoost演算法的流程圖:
對權重向量D更新,如果某個樣本被正確分類,那麼該樣本的權重改為:
計算出D後,AdaBoost繼續迭代重複訓練調整權重,直到訓練錯誤率為0或者弱分類器的資料達到使用者指定值為止。
4.1.3 完整AdaBoost演算法實現
虛擬碼
對每次迭代: 利用buildStump()函式找到最佳的單層決策樹 將最佳單層決策樹加入到單層決策樹陣列 計算alpha 計算新的權重向量D 更新累計類別估計值 如果錯誤率等於0.0,則退出迴圈
函式大致包括以下幾個:
1、基於單層決策樹的Adaboost訓練過程
2、Adaboost分類函式
如果我們需要在一個較為複雜的資料集中使用adaboost,最好還加上一個自適應資料載入函式。(注:程式碼均在本文結尾處統一放置)
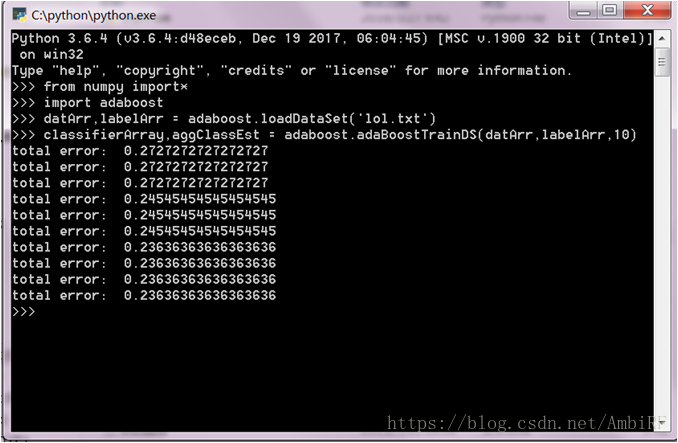
4.1.4 實際應用
在這裡需要注意的是AdaBoost需要確保標籤類別是+1和-1而非1和0,且自適應資料載入函式假定最後一個特徵是類別標籤,所以在這裡可以通過修改資料的txt文件或者是修改自適應資料載入函式來使得程式正常執行。(注:書中預設程式所限制所有資料應均為浮點數,所以在匯入任何資料庫的時候都應轉換成浮點數)結果:
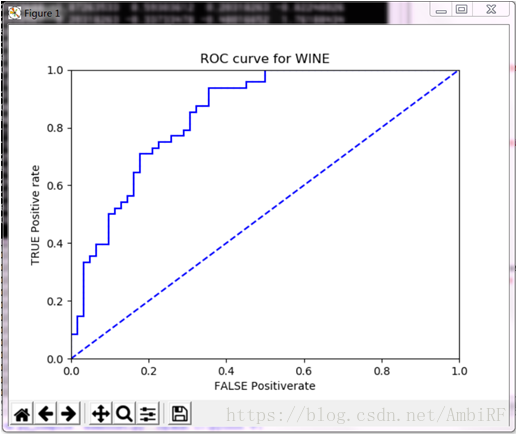
ROC曲線:
由最終結果可以看出,對於結果的預測可以達到75%的正確率,所以使用adaboost演算法是一個比較合適的選擇。
4.2 運用BP神經網路模型
4.2.1 模型簡介
BP(Back Propagation)神經網路是一種具有三層或者三層以上的多層神經網路,每一層都由若干個神經元組成,它的左、右各層之間各個神經元實現全連線,即左層的每一個神經元與右層的每個神經元都由連線,而上下各神經元之間無連線。BP神經網路按有導師學習方式進行訓練,當一對學習模式提供給神經網路後,其神經元的啟用值將從輸入層經各隱含層向輸出層傳播,在輸出層的各神經元輸出對應於輸入模式的網路響應。然後,按減少希望輸出與實際輸出誤差的原則,從輸出層經各隱含層,最後回到輸入層(從右到左)逐層修正各連線權。由於這種修正過程是從輸出到輸入逐層進行的,所以稱它為“誤差逆傳播演算法”。隨著這種誤差逆傳播訓練的不斷修正,網路對輸入模式響應的正確率也將不斷提高。
4.2.2 神經網路的概念
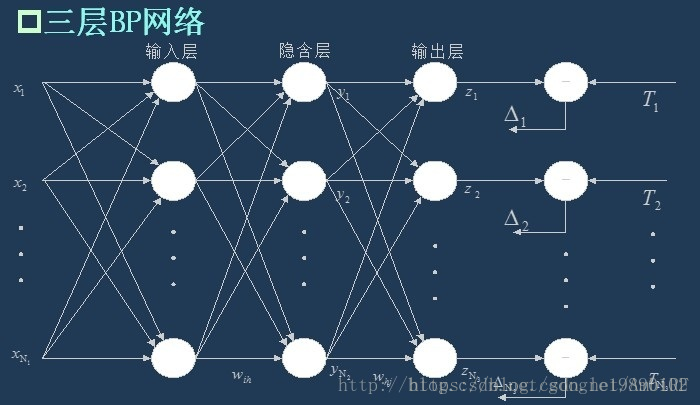
BP神經網路是一種多層的前饋神經網路,其主要的特點是:訊號是前向傳播的,而誤差是反向傳播的。具體來說,對於如下的只含一個隱層的神經網路模型:
BP神經網路的過程主要分為兩個階段,第一階段是訊號的前向傳播,從輸入層經過隱含層,最後到達輸出層;第二階段是誤差的反向傳播,從輸出層到隱含層,最後到輸入層,依次調節隱含層到輸出層的權重和偏置,輸入層到隱含層的權重和偏置。
4.2.3神經網路的流程
假設輸入層的節點個數為如上面的三層BP網路所示,隱含層的輸出
輸出層的輸出為
我們取誤差公式為:
其中
以上公式中,
再判斷演算法是否已經收斂,常見的有指定迭代的代數,判斷相鄰的兩次誤差之間的差別是否小於指定的值等等。
4.2.4 程式實現
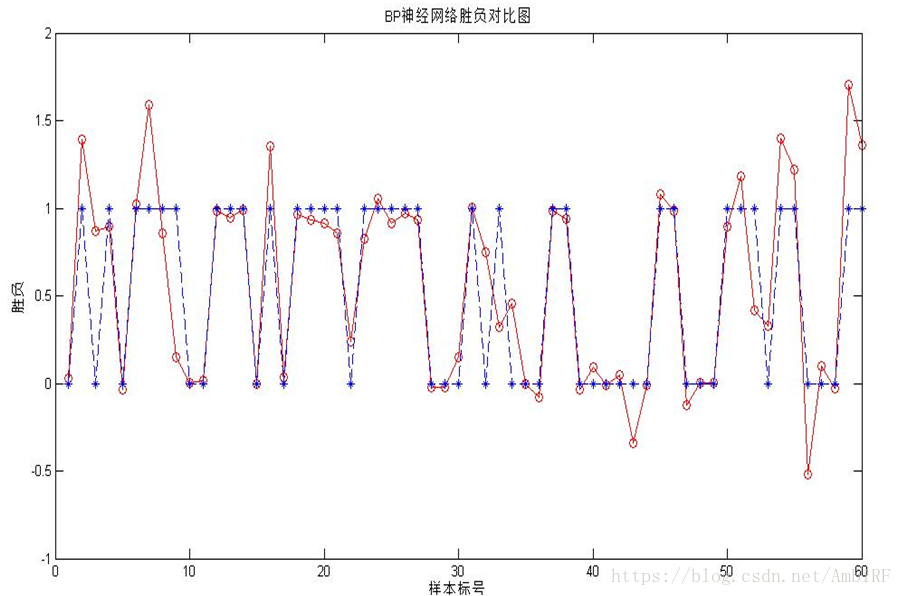
因為我對python運用還不算十分熟悉,在運用神經網路的時候,我使用的是MATLAB程式,執行結果如下:
可以看出雖然擬合的結果不錯,但仍然有些比較大的偏差,為此,我又在此基礎上嘗試了兩外一種神經網路的擬合。
4.3 廣義迴歸神經網路
4.3.1 基本簡介
GRNN神經網路 廣義迴歸神經網路(GRNN)是Donald FSpecht在1991年提出的。GRNN是一種正則化的徑向基網路,通常用來實現函式逼近。廣義迴歸神經網路是建立在數理統計基礎上的徑向基函式網路,其理論基礎是非線性迴歸分析。廣義迴歸神經網路對x的迴歸定義不同於徑向基函式的對高斯權值的最小二乘法疊加,他是利用密度函式來預測輸出。特點:訓練速度快,非線性對映能力強。
4.3.2 演算法流程
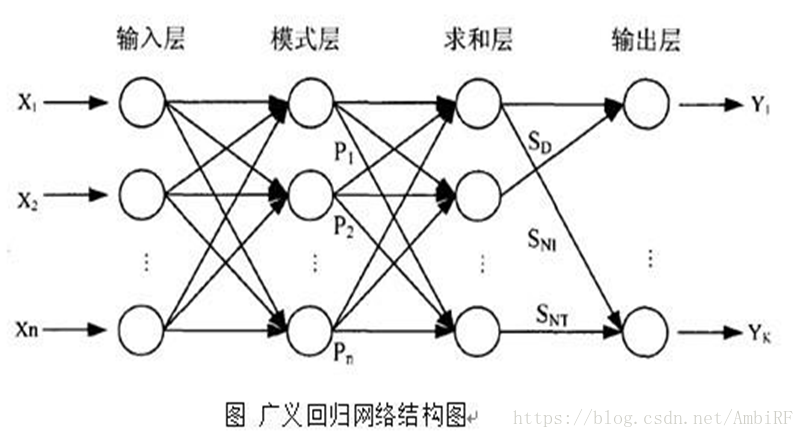
GRNN 在結構上由四層構成,分別為輸入層、模式層、 求和層和輸出層。
1.輸入層為向量,維度為m,樣本個數為n,線性函式為傳輸函式。
2.隱藏層與輸入層全連線,層內無連線,隱藏層神經元個數與樣本個數相等,也就是n,傳輸函式為徑向基函式。
3.加和層中有兩個節點,第一個節點為每個隱含層節點的輸出和,第二個節點為預期的結果與每個隱含層節點的加權和。
4.輸出層輸出是第二個節點除以第一個節點。
4.3.3 模型實踐
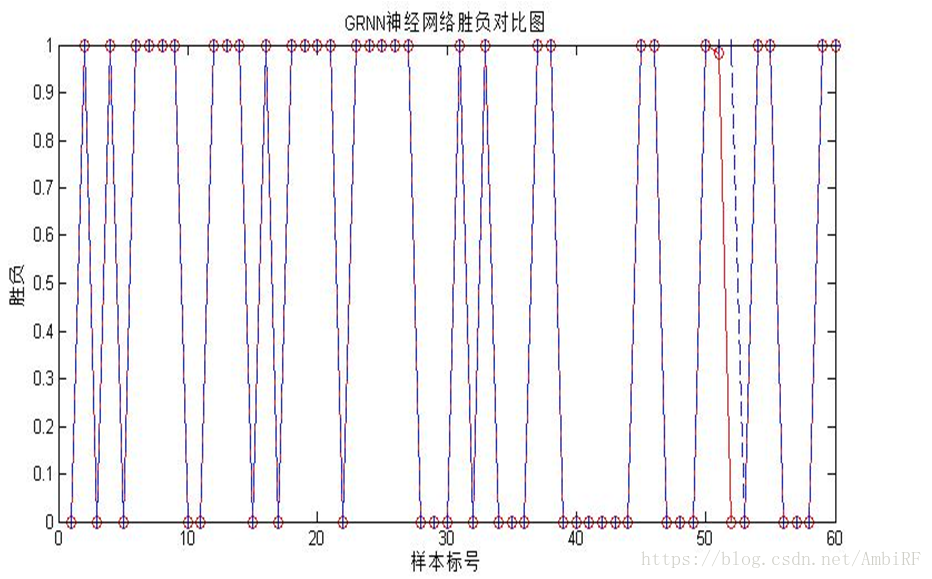
GRNN神經網路訓練效果:紅色網路輸出資料 藍色實際資料
從最後的結果可以看出相比於BP神經網路而言,廣義迴歸網路更適合這個資料集。
五、總結及心得
這是我真正意義上第一次選擇一個從未有過的資料集進行預測,從最開始原始資料的查詢和分析,到資料視覺化和特徵值的選擇,對我來說都是不小的考驗。在今年進行學習的《機器學習》這門課程中我學到最多的並不是與機器學習相關的內容,而是接受了一種全新的自學模式。我想這種學習模式對於我們的求知慾和創造性的激發是正常上課所給與不了的,也和國外的教學模式不謀而合。這個學期我曾經無數次的為了弄明白一個程式段所包含的意義不眠不休,但是最後看到預測結果的合理的時候讓我局的一切的辛苦都是值得的。在今後的學習中,我可能會出國讀研轉換學習方向重點學習人工智慧這一專業,有了這一學期的入門和鋪墊,我會更加快速地適應這門科學。最後,我要感謝老師和助教不厭其煩給我幫助和解答,感謝!
參考資料:
CSDN——Adaboost 2.24號:ROC曲線的繪製和AUC計算函式
CSDN——AdaBoost--從原理到實現
中國郵電出版社——《機器學習實戰》
CSDN——神經網路學習筆記(六) 廣義迴歸神經網路 https://blog.csdn.net/cyhbrilliant/article/details/52694943CSDN——【通俗講解】BP神經網路 https://blog.csdn.net/guomutian911/article/details/78635617
程式碼實現:
from numpy import *
import matplotlib.pyplot as plt
def loadSimpData():
datMat = matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels
def loadDataSet(fileName): #general function to parse tab -delimited floats
numFeat = len(open(fileName).readline().split('\t')) #get number of fields
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print ("total error: ",errorRate)
if errorRate == 0.0: break
return weakClassArr,aggClassEst
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print (aggClassEst)
return sign(aggClassEst)
def plotROC(predStrengths, classLabels):
import matplotlib.pyplot as plt
cur = (1.0,1.0) #cursor
ySum = 0.0 #variable to calculate AUC
numPosClas = sum(array(classLabels)==1.0)
yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
#loop through all the values, drawing a line segment at each point
for index in sortedIndicies.tolist()[0]:
if classLabels[index] == 1.0:
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0;
ySum += cur[1]
#draw line from cur to (cur[0]-delX,cur[1]-delY)
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
cur = (cur[0]-delX,cur[1]-delY)
ax.plot([0,1],[0,1],'b--')
plt.xlabel('FALSE Positiverate'); plt.ylabel('TRUE Positive rate')
plt.title('ROC curve for WINE')
ax.axis([0,1,0,1])
plt.show()
print ("the Area Under the Curve is: ",ySum*xStep)