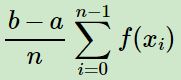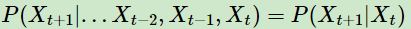蒙特卡羅 馬爾科夫鏈 與Gibbs取樣
這幾個概念看了挺多遍都還是含混不清,最近看了幾篇部落格,才算大致理解了一點點皮毛,所以來總結一下。
MCMC概述
從名字我們可以看出,MCMC由兩個MC組成,即蒙特卡羅方法(Monte Carlo Simulation,簡稱MC)和馬爾科夫鏈(Markov Chain ,也簡稱MC)。要弄懂MCMC的原理我們首先得搞清楚蒙特卡羅方法和馬爾科夫鏈的原理
蒙特卡羅方法是一種隨機模擬的方法,最早的蒙特卡羅方法是用來求積分的。通常我們可以用下面的方法求積分
但這個公式是假定x在[a, b]之間均勻分佈的,而實際情況中絕大部分都是非均勻分佈的,所以如果我們可以得到x的概率分佈函式p(x),那麼就可以用下面的式子求積分
所以如果求出了x的概率分佈,我們可以基於概率分佈去取樣基於這個概率分佈的n個x的樣本集,帶入蒙特卡羅求和的式子即可求解。那麼我們現在的問題轉到了如何求出x的分佈p(x)對應的若干個樣本f(xi)。
對於常見的均勻分佈uniform(0,1)是非常容易取樣樣本的,一般通過線性同餘發生器可以很方便的生成(0,1)之間的偽隨機數樣本。而其他常見的概率分佈,無論是離散的分佈還是連續的分佈,它們的樣本都可以通過uniform(0,1)的樣本轉換而得。
不過很多時候,我們的x的概率分佈不是常見的分佈,這意味著我們沒法方便的得到這些非常見的概率分佈的樣本集。對於概率分佈不是常見的分佈,一個可行的辦法是採用接受-拒絕取樣來得到該分佈的樣本。既然 p(x) 太複雜在程式中沒法直接取樣,那麼我設定一個程式可採樣的分佈 q(x) 比如高斯分佈,然後按照一定的方法拒絕某些樣本,以達到接近 p(x) 分佈的目的,其中q(x)叫做 proposal distribution。
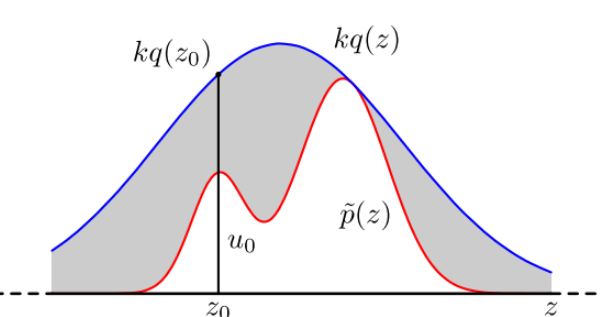
具體採用過程如下,設定一個方便取樣的常用概率分佈函式 q(x),以及一個常量 k,使得 p(x) 總在 kq(x) 的下方。如上圖。
首先,取樣得到q(x)的一個樣本z0,取樣方法如第三節。然後,從均勻分佈(0,kq(z0))中取樣得到一個值u。如果u落在了上圖中的灰色區域,則拒絕這次抽樣,否則接受這個樣本z0。重複以上過程得到n個接受的樣本z0,z1,...zn−1,則最後的蒙特卡羅方法求解結果為:
整個過程中,我們通過一系列的接受拒絕決策來達到用q(x)模擬p(x)概率分佈的目的。
蒙特卡羅方法小結
使用接受-拒絕取樣,我們可以解決一些概率分佈不是常見的分佈的時候,得到其取樣集並用蒙特卡羅方法求和的目的。但是接受-拒絕取樣也只能部分滿足我們的需求,在很多時候我們還是很難得到我們的概率分佈的樣本集。比如:
2)對於一些高維的複雜非常見分佈p(x1,x2,...,xn),我們要找到一個合適的q(x)和k非常困難。
從上面可以看出,要想將蒙特卡羅方法作為一個通用的取樣模擬求和的方法,必須解決如何方便得到各種複雜概率分佈對應的取樣樣本集的問題。而馬爾科夫鏈正好可以幫助我們找到這些複雜概率分佈對應的取樣樣本集。
馬爾科夫鏈定義本身比較簡單,它假設某一時刻狀態轉移的概率只依賴於它的前一個狀態。如果用精確的數學定義來描述,則假設我們的序列狀態是...Xt−2,Xt−1,Xt,Xt+1,...,那麼我們的在時刻Xt+1的狀態的條件概率僅僅依賴於時刻Xt,即:
既然某一時刻狀態轉移的概率只依賴於它的前一個狀態,那麼我們只要能求出系統中任意兩個狀態之間的轉換概率,這個馬爾科夫鏈的模型就定了。
那麼馬爾科夫鏈模型的狀態轉移矩陣和我們蒙特卡羅方法需要的概率分佈樣本集有什麼關係呢?這需要從馬爾科夫鏈模型的狀態轉移矩陣的性質講起。
馬爾科夫鏈模型狀態轉移矩陣的性質
馬爾科夫鏈模型的狀態轉移矩陣收斂到的穩定概率分佈與我們的初始狀態概率分佈無關。這是一個非常好的性質,也就是說,如果我們得到了這個穩定概率分佈對應的馬爾科夫鏈模型的狀態轉移矩陣,則我們可以用任意的概率分佈樣本開始,帶入馬爾科夫鏈模型的狀態轉移矩陣,這樣經過一些序列的轉換,最終就可以得到符合對應穩定概率分佈的樣本。
同時,對於一個確定的狀態轉移矩陣P,它的n次冪Pn在當n大於一定的值的時候也可以發現是確定的。
用數學語言總結下馬爾科夫鏈的收斂性質如下。
π 通常稱為馬爾科夫鏈的平穩分佈。
所以基於馬爾科夫鏈取樣如下。
1)輸入馬爾科夫鏈狀態轉移矩陣P,設定狀態轉移次數閾值n1,需要的樣本個數n2
2)從任意簡單概率分佈取樣得到初始狀態值x0
3)for t=0 to n1+n2−1: 從條件概率分佈P(x|xt)中取樣得到樣本xt+1
樣本集(xn1,xn1+1,...,xn1+n2−1)即為我們需要的平穩分佈對應的樣本集。
所以,如果假定我們可以得到我們需要取樣樣本的平穩分佈所對應的馬爾科夫鏈狀態轉移矩陣,那麼我們就可以用馬爾科夫鏈取樣得到我們需要的樣本集,進而進行蒙特卡羅模擬。但是一個重要的問題是,隨意給定一個平穩分佈π,如何得到它所對應的馬爾科夫鏈狀態轉移矩陣P呢?MCMC取樣通過迂迴的方式解決了這個問題。
在解決從平穩分佈π, 找到對應的馬爾科夫鏈狀態轉移矩陣P之前,我們還需要先看看馬爾科夫鏈的細緻平穩條件。定義如下。如果非週期馬爾科夫鏈的狀態轉移矩陣P和概率分佈π(x)對於所有的i,j滿足:π(i)P(i,j)=π(j)P(j,i),則稱概率分佈π(x)是狀態轉移矩陣P的平穩分佈。證明很簡單,即
將上式用矩陣表示即為:πP=π
可以發現馬爾科夫鏈的細緻平穩條件滿足馬爾可夫鏈的收斂性質。也就是說,只要我們找到了可以使概率分佈π(x)滿足細緻平穩分佈的矩陣P即可。這給了我們尋找從平穩分佈π, 找到對應的馬爾科夫鏈狀態轉移矩陣P的新思路。但不幸的是,我們的目標平穩分佈是π(x),隨機找一個馬爾科夫鏈狀態轉移矩陣Q,它是很難滿足細緻平穩條件的。即π(i)Q(i,j)≠π(j)Q(j,i)。
MCMC取樣
由於一般情況下,目標平穩分佈π(x)和某一個馬爾科夫鏈狀態轉移矩陣Q不滿足細緻平穩條件,我們可以對公式π(i)P(i,j)=π(j)P(j,i)做一個改造,使細緻平穩條件成立。方法是引入一個α(i,j),使上式可以取等號,即:
α(i,j)滿足α(i,j)=π(j)Q(j,i) α(j,i)=π(i)Q(i,j)
我們就得到了我們的分佈π(x)對應的馬爾科夫鏈狀態轉移矩陣P,滿足:
也就是說,我們的目標矩陣P可以通過任意一個馬爾科夫鏈狀態轉移矩陣Q乘以α(i,j)得到。α(i,j)我們有一般稱之為接受率。取值在[0,1]之間,可以理解為一個概率值。即目標矩陣P可以通過任意一個馬爾科夫鏈狀態轉移矩陣Q以一定的接受率獲得。
MCMC的取樣過程如下:
1)輸入我們任意選定的馬爾科夫鏈狀態轉移矩陣Q,平穩分佈π(x),設定狀態轉移次數閾值n1,需要的樣本個數n2
2)從任意簡單概率分佈取樣得到初始狀態值x0
3)for t=0 to n1+n2−1:
a) 從條件概率分佈Q(x|xt)中取樣得到樣本x∗
b) 從均勻分佈取樣u∼uniform[0,1]
c) 如果u<α(xt,x∗)=π(x∗)Q(x∗,xt), 則接受轉移xt→x∗,即xt+1=x∗
d) 否則不接受轉移,t=max(t−1,0)
樣本集(xn1,xn1+1,...,xn1+n2−1)即為我們需要的平穩分佈對應的樣本集。
上面這個過程基本上就是MCMC取樣的完整取樣理論了,但是這個取樣演算法還是比較難在實際中應用,問題在上面第三步的c步驟,接受率這兒。由於α(xt,x∗)可能非常的小,比如0.1,導致我們大部分的取樣值都被拒絕轉移,取樣效率很低。有可能我們取樣了上百萬次馬爾可夫鏈還沒有收斂,也就是上面這個n1要非常非常的大,這讓人難以接受。這時M-H取樣出場了。
M-H取樣
M-H取樣是Metropolis-Hastings取樣的簡稱,這個演算法首先由Metropolis提出,被Hastings改進,因此被稱之為Metropolis-Hastings取樣或M-H取樣。M-H取樣解決了我們上一節MCMC取樣接受率過低的問題。
將接受率可以做如下改進,即:
通過這個微小的改造,我們就得到了可以在實際應用中使用的M-H取樣演算法過程如下:
1)輸入我們任意選定的馬爾科夫鏈狀態轉移矩陣Q,平穩分佈π(x),設定狀態轉移次數閾值n1,需要的樣本個數n2
2)從任意簡單概率分佈取樣得到初始狀態值x0
3)for t=0 to n1+n2−1:
a) 從條件概率分佈Q(x|xt)中取樣得到樣本x∗
b) 從均勻分佈取樣u∼uniform[0,1]
c) 如果u<α(xt,x∗)=min{ π(j)Q(j,i) / π(i)Q(i,j), 1}, 則接受轉移xt→x∗,即xt+1=x∗
d) 否則不接受轉移,t=max(t−1,0)
樣本集(xn1,xn1+1,...,xn1+n2−1)即為我們需要的平穩分佈對應的樣本集。
很多時候,我們選擇的馬爾科夫鏈狀態轉移矩陣Q如果是對稱的,即滿足Q(i,j)=Q(j,i),這時我們的接受率可以進一步簡化為:
α(i,j)=min{ π(j) / π(i), 1}
M-H取樣總結
M-H取樣完整解決了使用蒙特卡羅方法需要的任意概率分佈樣本集的問題,因此在實際生產環境得到了廣泛的應用。但是在大資料時代,M-H取樣面臨著兩大難題:
1) 我們的資料特徵非常的多,M-H取樣由於接受率計算式π(j)Q(j,i)/π(i)Q(i,j)的存在,在高維時需要的計算時間非常的可觀,演算法效率很低。同時α(i,j)一般小於1,有時候辛苦計算出來卻被拒絕了。能不能做到不拒絕轉移呢?
2) 由於特徵維度大,很多時候我們甚至很難求出目標的各特徵維度聯合分佈,但是可以方便求出各個特徵之間的條件概率分佈。這時候我們能不能只有各維度之間條件概率分佈的情況下方便的取樣呢?
Gibbs取樣解決了上面兩個問題,因此在大資料時代,MCMC取樣基本是Gibbs取樣的天下。
重新尋找合適的細緻平穩條件
利用上一節找到的狀態轉移矩陣,我們就得到了二維Gibbs取樣,這個取樣需要兩個維度之間的條件概率。具體過程如下:
1)輸入平穩分佈π(x1,x2),設定狀態轉移次數閾值n1,需要的樣本個數n2
2)隨機初始化初始狀態值x1(0)和x2(0)
3)for t=0 to n1+n2−1:
a) 從條件概率分佈P(x2|x1(t))中取樣得到樣本x2(t+1)
b) 從條件概率分佈P(x1|x2(t+1))中取樣得到樣本x1(t+1)
樣本集

當然,座標軸輪換不是必須的,我們也可以每次隨機選擇一個座標軸進行取樣。不過常用的Gibbs取樣的實現都是基於座標軸輪換的。
多維Gibbs取樣
上面的這個演算法推廣到多維的時候也是成立的。比如一個n維的概率分佈π(x1,x2,...xn),我們可以通過在n個座標軸上輪換取樣,來得到新的樣本。對於輪換到的任意一個座標軸xi上的轉移,馬爾科夫鏈的狀態轉移概率為P(xi|x1,x2,...,xi−1,xi+1,...,xn),即固定n−1個座標軸,在某一個座標軸上移動。
具體的演算法過程如下:
1)輸入平穩分佈π(x1,x2,...,xn)或者對應的所有特徵的條件概率分佈,設定狀態轉移次數閾值n1,需要的樣本個數n22)隨機初始化初始狀態值(x(0)1,x(0)2,...,x(0)n
3)for t=0 to n1+n2−1:
a) 從條件概率分佈P(x1|x2(t),x3(t),...,xn(t))中取樣得到樣本x1(t+1)
b) 從條件概率分佈P(x2|x1(t+1),x3(t),x4(t),...,xn(t))中取樣得到樣本x2(t+1)
c)...
d) 從條件概率分佈P(xj|x1(t+1),x2(t+1),...,xj−1(t+1),xj+1(t)...,xn(t))中取樣得到樣本xj(t+1)
e)...
f) 從條件概率分佈P(xn|x1(t+1),x2(t+1),...,xn-1(t+1))中取樣得到樣本xn(t+1)
樣本集{(x1(n1),x2(n1),...,xn(n1)),...,(x1(n1+n2−1),x2(n1+n2−1),...,xn(n1+n2−1))}即為我們需要的平穩分佈對應的樣本集。
整個取樣過程和Lasso迴歸的座標軸下降法演算法非常類似,只不過Lasso迴歸是固定n−1個特徵,對某一個特徵求極值。而Gibbs取樣是固定n−1個特徵在某一個特徵取樣。同樣的,輪換座標軸不是必須的,我們可以隨機選擇某一個座標軸進行狀態轉移,只不過常用的Gibbs取樣的實現都是基於座標軸輪換的。
至此,Gibbs取樣方法在沒有接受概率與特徵維度聯合分佈的情況下同樣完成了對任意概率分佈樣本集的取樣問題。
以下是自己結合全篇內容對MCMC,馬爾科夫鏈,Gibbs取樣這幾個問題之間關係的理解。 總結文章的整個思路就是要用蒙特卡羅方法求和,就得解決任意概率分佈樣本集的取樣問題,而由馬爾科夫鏈的性質可知,如果得到平穩分佈對應的狀態轉移矩陣P,那麼從任意初始狀態開始就可以用馬爾科夫鏈取樣得到我們需要的樣本集。問題在於隨意給定一個平穩分佈π,如何得到它所對應的馬爾科夫鏈狀態轉移矩陣P呢?這就是MCMC解決的問題。由於馬爾科夫的細緻平穩條件(如果非週期馬爾科夫鏈的狀態轉移矩陣P和概率分佈π(x)對於所有的i,j滿足:π(i)P(i,j)=π(j)P(j,i),則稱概率分佈π(x)是狀態轉移矩陣P的平穩分佈。)同樣滿足馬爾科夫鏈的收斂條件(πP=π),所以只要找到使π(x)滿足細緻平穩條件的P,也就是找到了狀態轉移矩陣P。由於對一個π(x)很難隨機找到一個馬爾科夫狀態轉移矩陣Q滿足細緻平穩分佈,所以通過改進,引入接受率α(i,j),可以得到P(i,j)=Q(i,j)α(i,j),所以我們的目標矩陣P可以通過任意一個馬爾科夫鏈狀態轉移矩陣Q乘以α(i,j)得到。但同時由於α(i,j)太小,所以M-H方法做了改進。最後由於大資料背景下,在高維情況下,由於接受率的原因導致演算法收斂時間變長,再一個特徵的條件概率好計算然而聯合分佈概率卻不好計算,所以Gibbs取樣出現了。Gibbs取樣避開使用接受率與聯合分佈概率,直接採用條件分佈概率來得到任意概率分佈下的樣本,進而解決了任意概率分佈下的樣本採集問題。