[hiho]#1067 : 最近公共祖先·二 離線演算法
描述:(原題地址:http://hihocoder.com/problemset/problem/1067?sid=601284)
給定一顆樹,給出樹根,以及一些查詢pair,要求輸出每條查詢pair的最近公共節點。
保證所有查詢節點都在這棵樹上。
輸入:第一行一個整數N代表邊數,之後N行每行兩個節點分別是一對父子,其中第一對父子中的父節點是root。
之後是一個整數M代表查詢數,之後M行每行兩個節點代表一次查詢。1<=N,M<=10^5
輸出:對每一個查詢輸出一行結果。
樣例輸入:
4 Adam Sam Sam Joey Sam Micheal Adam Kevin 3 Sam Sam Adam Sam Micheal Kevin
Sam Adam Adam
其實一開始我是單純的。。單蠢的以為和線上演算法相同,嘗試採用標記法對每一個查詢只回溯一次,具體做法是這樣的:
class Node {
public:
Node *parent;
int flag;
string name;
};然並卵,一開始用map<string,string>和set<string>直接記錄關係和查詢路徑(5000ms)還是用unordered_map<string,string>加標記法(4000ms)還是用上面這個Node加標記法(3000ms),都是TLE。
無奈地看了提示,才發現原來離線演算法是這麼做的:
先收集所有查詢的資訊,然後對樹進行一次遍歷得到所有查詢的結果,然後輸出。
這聽起來有點不可思議,查詢是沒有規律的,怎麼遍歷一次就得到所有結果?做法是將具體的查詢分配給對應的節點,然後在遍歷過程中讓節點負責自己的查詢。
使用什麼遍歷?具有記錄祖先特性的遍歷就是深度遍歷啦。那麼遍歷到這個節點的時候怎麼做呢?依然是標記的方法:一開始所有節點都是白色的,當來到這個節點時,將其標記為灰色;當離開它時,將其標記為黑色。如下圖(引自hihoCoder)
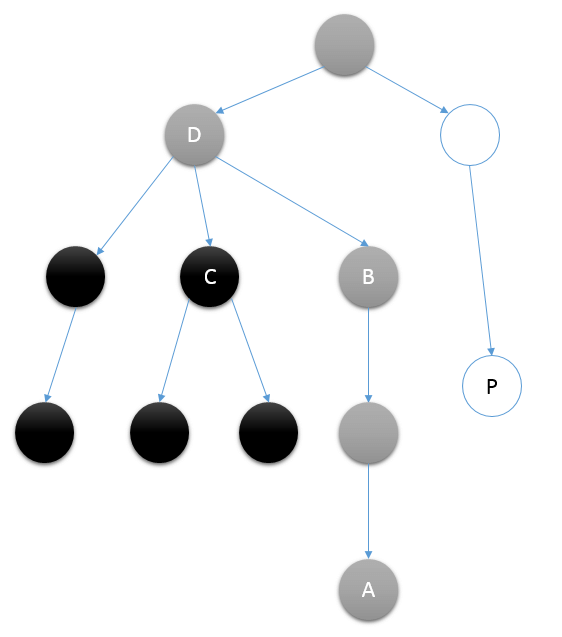
此刻我們來到A節點,那麼可能有三種查詢:AB,AC和AP,分別對應另一個要匹配的節點在自己到root的路徑上(正在訪問)、已經去過(訪問過)和還沒經過(未訪問過)的節點。
如果是B,很簡單直接記錄B即可。
如果是P,沒法判斷,可以將查詢交給P,自己不處理。
如果是C,則需要找到一個灰色的節點是C的最近祖先。如果要循著邊往上找,比如在查詢PA時,讓A順著父節點一直向上找到根,那時間複雜度也是比較大的。不過這可以利用等價類(並查集)演算法的技巧,即為每一個節點標記其所屬的集合,一開始所有節點都屬於自己的集合;當離開一個節點的時候,它要變成黑色了,它的父節點還是灰色,此時將它所屬的集合改為其父節點即可。查詢的時候遇到黑色的節點,則直接去找其所屬集合,如果所屬集合為自身則直接返回;‘否則將其沿路所有集合都改成最終所屬的集合。還是比如PA,將從A到根的所有節點的所屬集合都改成根,以後的查詢就可以直接得到結果了。
遍歷完成之後,所有查詢也完成了,然後依次輸出就可以啦。中間忘記進行“將其沿路所有集合都改成最終所屬的集合”這一步操作(2000ms)再次導致超時,改正之後(1000ms)就AC了。看起來很複雜,寫起來發現其實邏輯理順了還是比較簡潔的。
程式碼如下:
// Problems.cpp : Defines the entry point for the console application.
//
#include <sstream>
#include <stdio.h>
#include <functional>
#include <string.h>
#include <iomanip>
#include <time.h>
#include <math.h>
#include <fstream>
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
#include <tuple>
#include <map>
#include <string>
#include <set>
#include <algorithm>
#include <list>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int MAXPRIME = 1000000007;
class Node {
public:
static unordered_map<string, Node*> mp;
string name;
char c;
Node *belong;
vector<Node*> children;
unordered_map<string, Node*> query;
Node(string n) : name(n), c(0), belong(this) {}
Node* getBelong() {
if (belong == this) return belong;
belong = belong->getBelong();
return belong;
}
};
unordered_map<string, Node*> Node::mp;
void dfs(Node *root) {
root->c = 1;
// do query
for (auto &i : root->query) {
Node *p = Node::mp[i.first];
if (p->c == 1) { // visiting
i.second = p;
}
else if (p->c == 2) { // visited
i.second = p->getBelong();
}
else { // not visited
p->query[root->name] = NULL; // leave it to the other
}
}
// dfs
for (auto &i : root->children) {
dfs(i);
i->belong = root->belong;
}
root->c = 2;
}
void pro() {
int n;
cin >> n;
string a, b;
Node *root = NULL;
n--;
cin >> a >> b;
root = new Node(a);
Node::mp[a] = root;
Node::mp[b] = new Node(b);
root->children.push_back(Node::mp[b]);
while (n--) {
cin >> a >> b;
if (Node::mp.find(a) == Node::mp.end()) Node::mp[a] = new Node(a);
if (Node::mp.find(b) == Node::mp.end()) Node::mp[b] = new Node(b);
Node::mp[a]->children.push_back(Node::mp[b]);
}
vector<pair<string, string>> q;
cin >> n;
Node *pa, *pb;
while (n--) {
cin >> a >> b;
pa = Node::mp[a], pb = Node::mp[b];
q.push_back(make_pair(a, b));
pa->query[b] = NULL;
}
dfs(root);
for (auto &i : q) {
pa = Node::mp[i.first], pb = Node::mp[i.second];
if (pa->query[i.second]) {
cout << pa->query[i.second]->name << endl;
} else {
cout << pb->query[i.first]->name << endl;
}
}
}
void handle() {
pro();
}
int main() {
handle();
system("PAUSE");
return 0;
}
