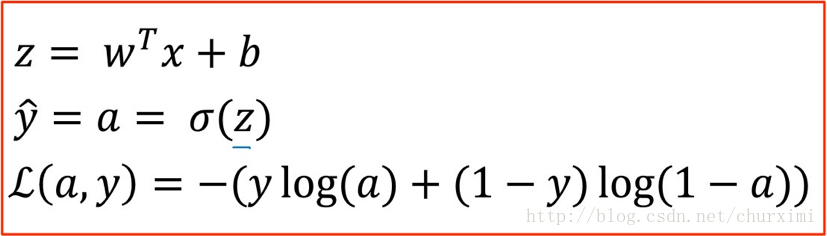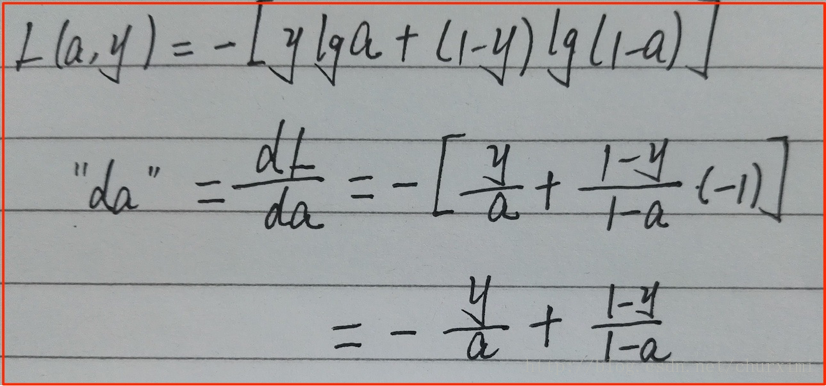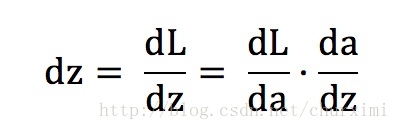吳恩達《deeplearning深度學習》課程學習筆記【1】(精簡總結)
阿新 • • 發佈:2019-01-06
畢業以後就沒再寫過部落格,又想起來了。
Ps:本文只是個人筆記總結,沒有大段的詳細講解,僅僅是將自己不熟悉和認為重要的東西總結下來,算是一個大綱,用的時候方便回憶和查詢。
Ps2:部分筆記內容見圖片。
相關課程內容
一、神經網路和深度學習
- 第一週 深度學習概論
- 第二週 神經網路基礎
知識點總結
1. 神經網路
- 神經元:neuron
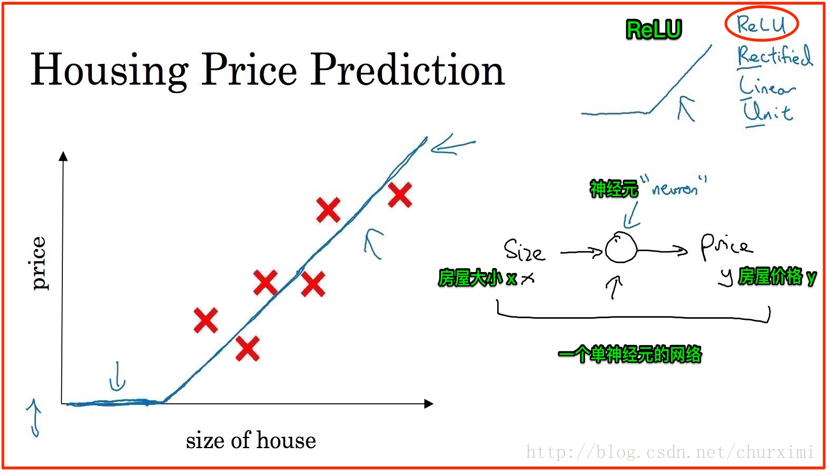
2. 房屋價格預測
- 若干輸入特徵→輸出
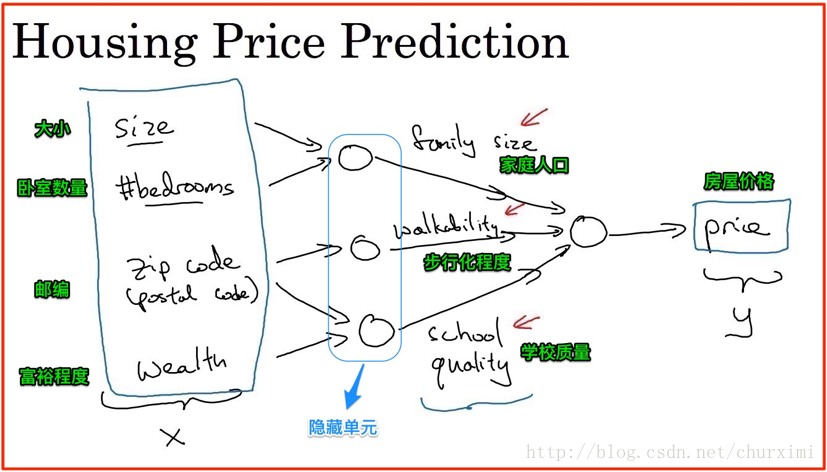
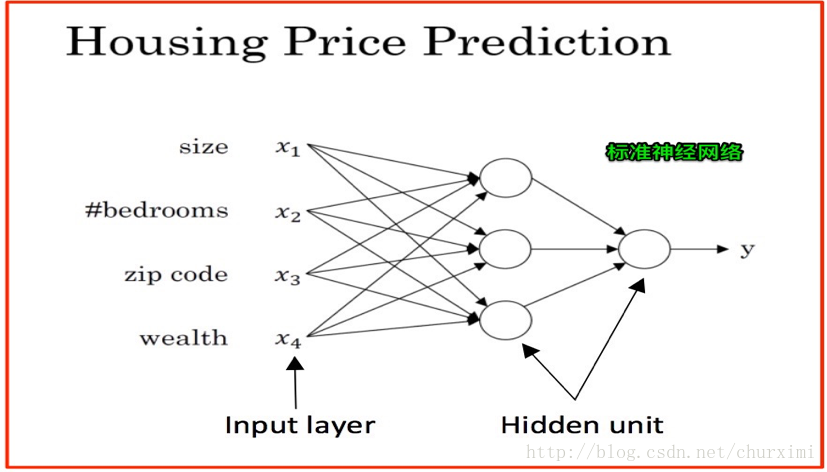
3. 標準神經網路
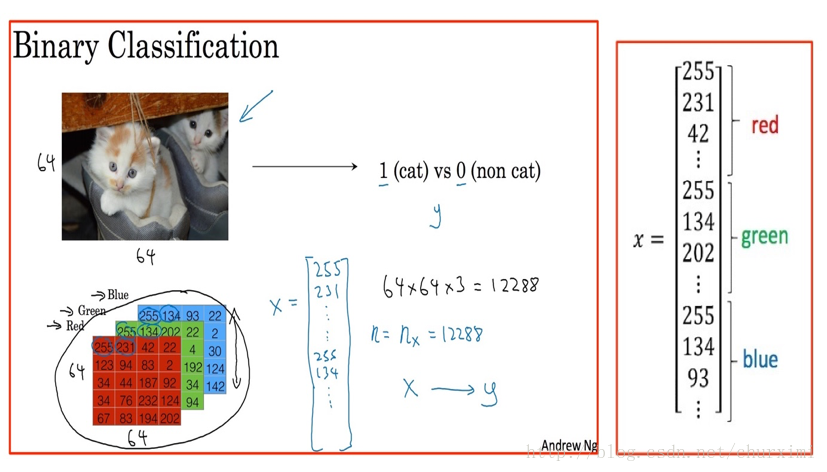
4. 貓的影象識別
- 二元分類
- 邏輯迴歸
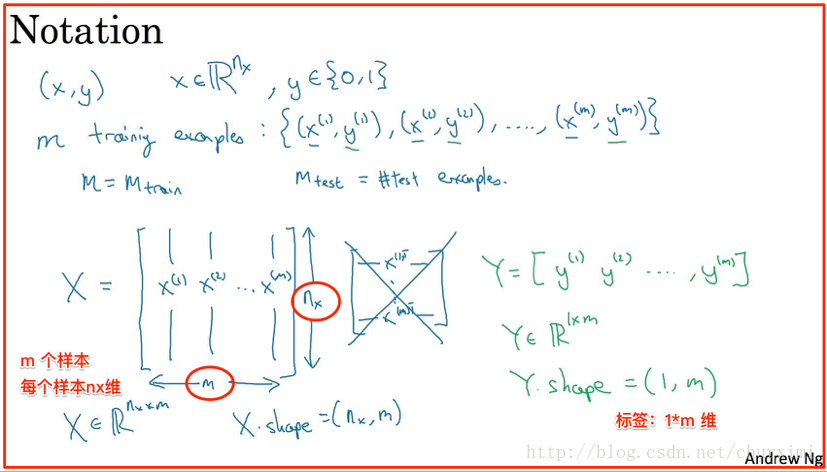
(1)影象表示/轉換
(2)資料集表示
- X維度:(n, m)
- Y維度:(1, m)
5. 啟用函式

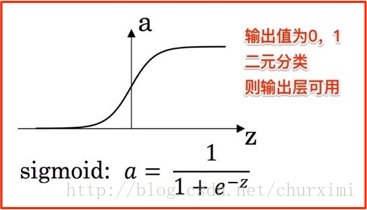
(1)Sigmoid函式(可以作二元分類輸出層啟用函式)及tanh函式
- 在Sigmoid函式和tanh函式(雙曲正切)兩端的斜率很小,梯度接近於0,在使用梯度下降法時,引數變化會非常緩慢,因此學習會變得非常緩慢。
- tanh函式通常比Sigmoid函式表現好。
(2)ReLU函式
- 對於所有的正值,斜率都為1。 大多數地方斜率遠離0,能夠使梯度下降法執行得更快。 缺點是左側導數為0。
- 線性修正單元(Rectified Linear Unit),修正:取不小於0的值。
6. 成本函式(cost function)
- 衡量引數W和b在全部訓練集上的效果。
- 成本函式是損失函式在全部訓練集上的平均值。
- 成本函式計算公式如下:
7. 損失函式(Loss function)/誤差函式(error function)
- 用於衡量單一訓練樣例預測輸出值y_hat與實際值y的差距。
- 例如:誤差平方可以用,但是不適合梯度下降法。
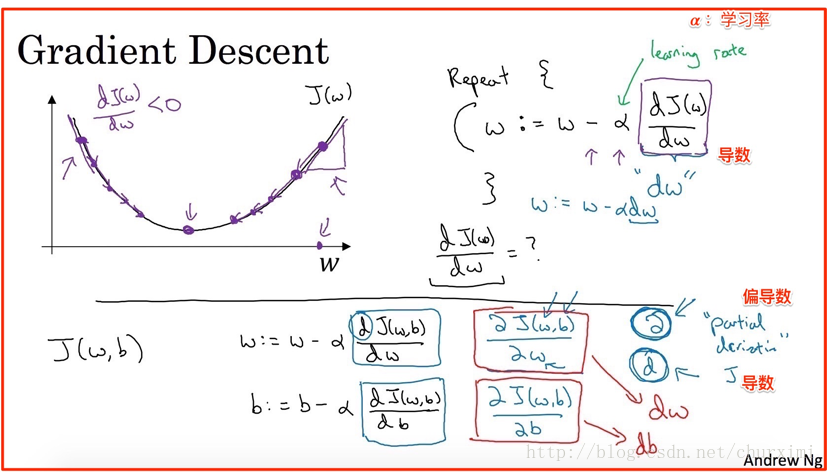
8. 梯度下降法(Gradient Descent)
我們需要找到能夠使成本函式J(W, b)最小化的引數W和b。
(1)隨機化一個初始點(例如全0)
(2)朝最陡的下坡方向走一步
(3)經過N次迭代後到達/接近全域性最優解(global optimum)
- 凸函式(convex):
- 非凸函式(non-convex):有很多不同的區域性最優
9. 導數
- 梯度下降法,需要計算成本函式J(W, b)對各個引數(W,b等)的導數。
正向計算:
計算損失函式L(a, y)對引數a,z,w,b的導數:
(1)★★★ da計算:
(2)★★★ dz計算:(結果為a-y)
- 鏈式法則:
- 【第一項】dL/da上面已經計算出來了
【第二項】da/dz即為啟用函式求導
a的公式(Sigmoid函式):
sigmoid函式求導:
- 最終dz = 【第一項】·【第二項】= a - y
(3)★★★ dw,db計算:
- dw1 = x1 * dz
- dw2 = x2 * dz …
- dw = x * dz
- db = dz
10. 引數更新
- 最終da,dz,dw,db都能夠通過x,y,a來計算。
- 學習率α:learning rate(新的引數)
- w1 = w1 - α*dw1
- w2 = w2 - α*dw2
- b = b - α*db
11. m個樣本的梯度下降及向量化表示
- 成本函式 = sum(m個損失函式) / m
- dA,dZ,dW,db都能夠通過X,Y,A來計算,其中(X, Y)有m個。
- 注意點:
(1)W的轉置問題
(2)dW,db的計算要除以m取均值
(3)後續神經網路會有多層
12. 總結
- 公式不好輸入,下面是圖片