Part 1: 構建神經網路

歡迎來到本週的第一個作業，這個作業我們將利用numpy實現你的第一個迴圈神經網路。

迴圈神經網路(Recurrent Neural Networks: RNN) 因為有”記憶”，所以在自然語言處理(Natural Language Processing) 和其他序列化任務中非常有效。RNN每次讀取序列中的一個輸入x<t>$x^{<t>}$ (比如一個單詞), 通過啟用函式記住一些資訊和上下文，然後傳遞到下一個實踐部。這使得單向RNN可以攜帶資訊想前傳播，而雙向RNN更是可以攜帶過去的和未來的上下文資訊。

符號說明

• 上標 [l]${[l]}^{}$ 表示第l層
• 上標 (i)${(i)}^{}$ 表示第i個樣本
• 上標 <t>${<t>}^{}$ 表示輸入x在第t個時間步上的值
• 下標 i$i_{}$ 表示一個向量的第i個維度
• Tx$T_x$ 和 Ty$T_y$ 分別表示輸入和輸出的時間步數

導包

import numpy as np
from rnn_utils import *

下面是 rnn_utils 中包含的程式：

import numpy as np

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)


def sigmoid(x):
    return
 
 1 / (1 + np.exp(-x))


def initialize_adam(parameters) :
    """
    Initializes v and s as two python dictionaries with:
                - keys: "dW1", "db1", ..., "dWL", "dbL" 
                - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.

    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters["W" + str(l)] = Wl
                    parameters["b" + str(l)] = bl

    Returns: 
    v -- python dictionary that will contain the exponentially weighted average of the gradient.
                    v["dW" + str(l)] = ...
                    v["db" + str(l)] = ...
    s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                    s["dW" + str(l)] = ...
                    s["db" + str(l)] = ...

    """
 


    L = len(parameters) // 2 # number of layers in the neural networks
    v = {}
    s = {}

    # Initialize v, s. Input: "parameters". Outputs: "v, s".
    for l in range(L):
    ### START CODE HERE ### (approx. 4 lines)
        v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
        v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
        s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
        s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
    ### END CODE HERE ###

    return v, s


def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
                                beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8):
    """
    Update parameters using Adam

    Arguments:
    parameters -- python dictionary containing your parameters:
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    grads -- python dictionary containing your gradients for each parameters:
                    grads['dW' + str(l)] = dWl
                    grads['db' + str(l)] = dbl
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    learning_rate -- the learning rate, scalar.
    beta1 -- Exponential decay hyperparameter for the first moment estimates 
    beta2 -- Exponential decay hyperparameter for the second moment estimates 
    epsilon -- hyperparameter preventing division by zero in Adam updates

    Returns:
    parameters -- python dictionary containing your updated parameters 
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    """

    L = len(parameters) // 2                 # number of layers in the neural networks
    v_corrected = {}                         # Initializing first moment estimate, python dictionary
    s_corrected = {}                         # Initializing second moment estimate, python dictionary

    # Perform Adam update on all parameters
    for l in range(L):
        # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
        ### START CODE HERE ### (approx. 2 lines)
        v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1 - beta1) * grads["dW" + str(l+1)] 
        v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1 - beta1) * grads["db" + str(l+1)] 
        ### END CODE HERE ###

        # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - beta1**t)
        v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - beta1**t)
        ### END CODE HERE ###

        # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
        ### START CODE HERE ### (approx. 2 lines)
        s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1 - beta2) * (grads["dW" + str(l+1)] ** 2)
        s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1 - beta2) * (grads["db" + str(l+1)] ** 2)
        ### END CODE HERE ###

        # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1 - beta2 ** t)
        s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1 - beta2 ** t)
        ### END CODE HERE ###

        # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
        ### START CODE HERE ### (approx. 2 lines)
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)] / np.sqrt(s_corrected["dW" + str(l+1)] + epsilon)
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)] / np.sqrt(s_corrected["db" + str(l+1)] + epsilon)
        ### END CODE HERE ###

    return parameters, v, s

1 基本迴圈神經網路的前向傳播

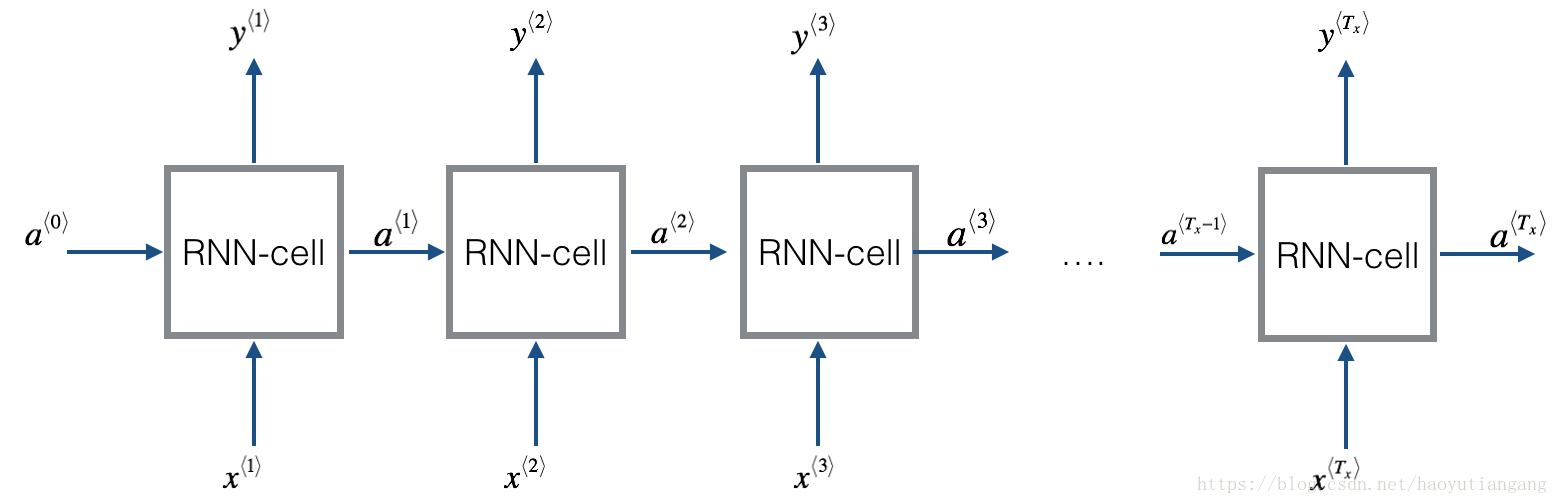
基本的RNN結構如下：(這裡Tx = Ty)

實現迴圈神經網路

• 實現 RNN 單時間步運算
• 按時間迴圈Tx的每個時間步運算

1.1 RNN 單元

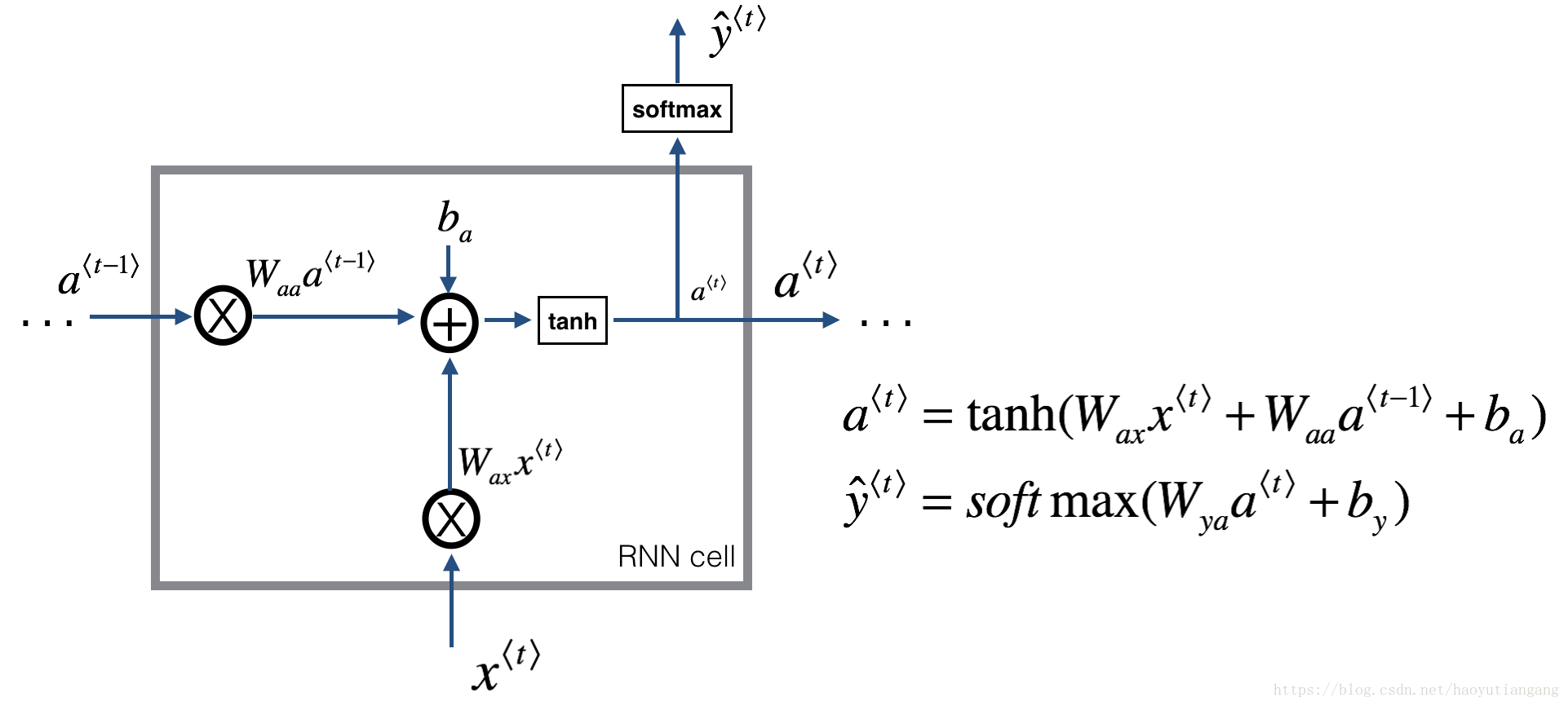
一個迴圈神經網路可以看成是單個RNN單元的重複。首先我們將實現一個單時間步的RNN單元的計算，下圖描述了單步RNN 的操作。

練習：實現上圖描述的單步RNN單元

1. 利用tanh啟用函式計算隱藏層的狀態
   a⟨t⟩=tanh(Waaa⟨t−1⟩+Waxx⟨t⟩+ba)$$a^{⟨t⟩}=\tanh (W_{aa}{a}^{⟨t-1⟩}+W_{ax}{x}^{⟨t⟩}+b_a)$$
2. 使用新的隱藏層狀態a<t>$a^{<t>}$ 計算預測值yhat$y_{hat}$ （已提供函式softmax）
   ŷ ⟨t⟩=softmax(Wyaa⟨t⟩+by)$${\hat{y}}^{⟨t⟩}=softmax(W_{ya}{a}^{⟨t⟩}+b_y)$$
3. 在cache中儲存引數
   (a⟨t⟩,a⟨t−1⟩,x⟨t⟩,parameters)$$(a^{⟨t⟩},a^{⟨t-1⟩},x^{⟨t⟩},parameters)$$
4. 返回 a<t>$a^{<t>}$, y<t>$y^{<t>}$ 和 cache

我們的輸入是m個向量。所以：x<t>$x^{<t>}$ 維度：(nx$n_x$, m) ; a<t>$a^{<t>}$ 維度：(na$n_a$, m)

# GRADED FUNCTION: rnn_cell_forward

def rnn_cell_forward(xt, a_prev, parameters):
    """
    Implements a single forward step of the RNN-cell as described in Figure (2)

    Arguments:
    xt -- your input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
    """

    # Retrieve parameters from "parameters"
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]

    ### START CODE HERE ### (≈2 lines)
    # compute next activation state using the formula given above
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    # compute output of the current cell using the formula given above
    yt_pred = softmax(np.dot(Wya, a_next) + by) 
    ### END CODE HERE ###

    # store values you need for backward propagation in cache
    cache = (a_next, a_prev, xt, parameters)

    return a_next, yt_pred, cache

#########################################################

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

# a_next[4] =  [ 0.59584544  0.18141802  0.61311866  0.99808218  0.85016201  # 0.99980978
#  -0.18887155  0.99815551  0.6531151   0.82872037]
# a_next.shape =  (5, 10)
# yt_pred[1] = [ 0.9888161   0.01682021  0.21140899  0.36817467  0.98988387  # 0.88945212
#   0.36920224  0.9966312   0.9982559   0.17746526]
# yt_pred.shape =  (2, 10)

期待輸出