題意：

講題的大佬說這題好簡單……
我個\(n^3\)暴力的不如退役吧……

思路：樹形DP，長鏈剖分

考慮把每組點的貢獻記錄在將三個點連成的路徑中深度最小的點上，如圖：

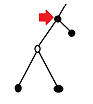
記\(f(x,d)\)為x子樹內與x的距離為d的點數，\(g(x,d)\)為x子樹內已經選了2個節點，最後一個節點與x的距離要為d的方案數。

則答案可以在dp的過程中統計出，且dp方程不難寫出：

\(g(x,j)+=f(x,j)\cdot f(v,j-1)+g(v,j+1)\)
\(f(x,j)+=f(v,j-1)\)

又發現這個dp過程在只有一個兒子節點時滿足：

\(f(x,d)=f(v,d-1)\)

\(g(x,d)=g(v,d+1)\)

於是可以想到長鏈剖分，O(1)繼承重兒子的資料。

具體實現用雙端佇列，因為雙端佇列支援首位push,pop，和隨機訪問（我也是今天才知道）

放程式碼：

#include<bits/stdc++.h>
#define rep(i,x,y) for (int i=(x);i<=(y);++i)
#define drep(i,y,x) for (int i=(y);i>=(x);--i)
#define go(x) for (int i=head[x];i;i=edge[i].nxt)
#define sz 50050
using namespace std;
typedef long long ll;
void file(){freopen("a.txt","r",stdin);}

int n;
struct hh{int t,nxt;}edge[sz<<1];
int head[sz],ecnt;
void make_edge(int f,int t)
{
    edge[++ecnt]=(hh){t,head[f]};
    head[f]=ecnt;
    edge[++ecnt]=(hh){f,head[t]};
    head[t]=ecnt;
}
ll ans;
deque<ll>f[sz],g[sz];
int rt[sz];
int D[sz],son[sz];
void dfs(int x,int fa)
{
    go(x) 
    {
        int v=edge[i].t;
        if (v==fa) continue;
        dfs(v,x);
        if (D[v]>=D[son[x]]) son[x]=v;
    }
    if (son[x]) D[x]=D[son[x]]+1;
    rt[x]=x;
    if (son[x])
    {
        rt[x]=rt[son[x]];
        g[rt[x]].pop_front();g[rt[x]].push_back(0);
    }
    int xx=x;x=rt[x];
    f[x].push_front(1);g[x].push_back(0);
    if (!son[xx]) return;
    go(xx) 
    {
        int vv=edge[i].t,v=rt[vv];
        if (vv==son[xx]||vv==fa) continue;
        rep(j,1,D[vv]+1)
        {
            ans+=g[x][j]*f[v][j-1]+(j>=D[vv]?0:f[x][j]*g[v][j+1]);
            g[x][j]+=f[x][j]*f[v][j-1]+(j>=D[vv]?0:g[v][j+1]);
            f[x][j]+=f[v][j-1];
        }
        if (D[vv]) g[x][0]+=g[v][1];
    }
    ans+=g[x][0];
}
int main()
{
    file();
    int x,y;
    while (233)
    {
        scanf("%d",&n);
        if (!n) break;
        rep(i,1,n) f[i].clear(),g[i].clear(),son[i]=D[i]=head[i]=0;
        ecnt=ans=0;
        rep(i,1,n-1) scanf("%d %d",&x,&y),make_edge(x,y);
        dfs(1,0);
        printf("%lld\n",ans);
    }
}
 

然而，這份程式碼開了O2後會RE，我也不知道為什麼……不過A了就好