第一次嘗試寫部落格，希望能堅持下去。。。
最近在做紅外小目標檢測，用到一個最大熵分割法，ok，下面介紹一下。

最大熵分割法

現在主要用的熵演算法有 P 氏熵演算法，KSW 熵演算法、JM 熵演算法下面以經典的 KSW 熵演算法為例介紹其原理和計算過程。

KSW熵演算法

設分割閾值為設分割閾值為t,

T為{0,1,2，...t}的灰度分佈，B為{t+1,t+2,...L-1}的灰度分佈，則概率分佈為：

式中

則這兩個概率密度相關的熵為：

定義函式φ（t）為H(T)和H（B）的和，則

求出φ(t)最大時的灰度級t即為所求的最佳閾值。

程式碼如下：

#include <cv.h>
#include <opencv2/opencv.hpp>  
#include <opencv2/legacy/legacy.hpp>
using namespace cv;

float calc_entropy(CvHistogram *hist, int begin, int end)
{
	float total = 0;  // 總概率
	// 得到總的Pi
	for(int i = begin; i < end; i++)
	{
		total += cvQueryHistValue_1D(hist,i);
	}

	float entropy = 0;  // 熵
	
	for(int i = begin; i < end; i++)
	{
		float probability = cvQueryHistValue_1D(hist, i);
		if(probability == 0)
			continue;
		probability /= total;

		entropy += -probability*log(probability);
	}

	return entropy;
}

int ksw_entropy(IplImage *img)
{
	assert(img != NULL);
	assert(img->depth == 8);  
    assert(img->nChannels == 1);  

	float range[2] = {0,255};
	float *ranges[1] = {&range[0]};
	int sizes = 256;

	// 建立直方圖
	CvHistogram *hist = cvCreateHist(1, &sizes, CV_HIST_ARRAY, ranges, 1);
	// 直方圖計算
	cvCalcHist(&img, hist, 0, 0);
	// 直方圖歸一化
	cvNormalizeHist(hist, 1.0); 

	int threshold = 0;
	float max_entropy = 0;
	// 迴圈計算，得到做大熵以及分割閾值
	for(int i = 0; i < sizes; i++)
	{
		float entropy = calc_entropy(hist, 0, i) + calc_entropy(hist, i+1, sizes);
		if(entropy > max_entropy)
		{
			max_entropy = entropy;
			threshold = i;
		}
	}

	return threshold;
}
int main(int argc, char **argv)
{
	IplImage *img = cvLoadImage("1.bmp", CV_LOAD_IMAGE_GRAYSCALE);
	IplImage *reimg = cvCreateImage(cvGetSize(img), IPL_DEPTH_8U, 1);

	int threshold = ksw_entropy(img);
	cvThreshold(img, reimg, threshold, 255, CV_THRESH_BINARY); 

	cvNamedWindow("img");
	cvShowImage("img", img);
	cvNamedWindow("reimg");
	cvShowImage("reimg", reimg);

	cvWaitKey(0);
	return 0;
}
 

在學習獲取灰度直方圖的時候，有一個函式讓我費解了半天，cvNormalizeHist,灰度歸一化，剛開始就是搞不懂這個灰度歸一化是指的什麼，

opencv給出的函式解釋如下：

什麼叫the sum of the bins becomes equal to factor，好吧，後來明白了，其實意思就是說，把直方圖縱座標的值相加的和等於第二個引數，所以如果設為1的話，那縱座標的值就是該灰度級的概率了。

下面是實驗圖片:

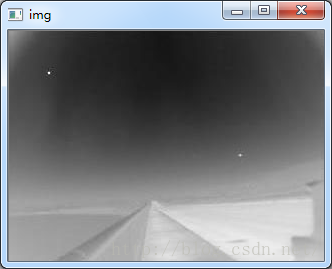
                                  圖1  原圖                                          圖2   最大熵閾值分割後圖片

效果很不理想吧，所以在做閾值分割前需要加入tophat，後面部落格會講到。

全文完。