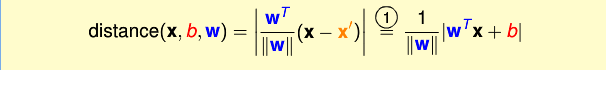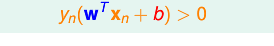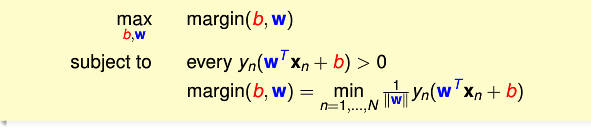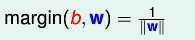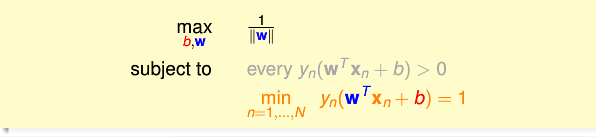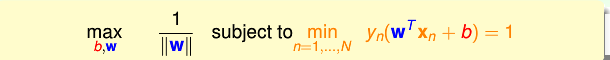svm系列之最大分隔超平面
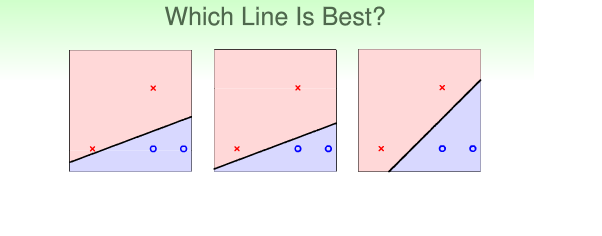
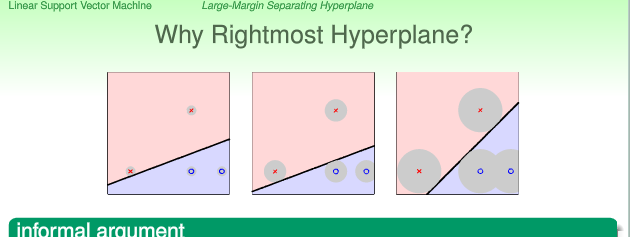
對於對上面4點的分隔,如果是用線性迴歸的話,三個圖形都可能發生。因為PLA是遇到一個輸入值,才進行調整,即如果用PLA模型的話,最終的模型與初始狀態和輸入點的順序有關。都是我們從直覺上來看,不難發現,其實最右邊的分割線由於另外兩個分割線的。
那為什麼最右邊的超平面是最好的呢???
現在,我們先來一個直觀的理解。
在這裡我們先假設資料是可分。
以上有4個點,我們要對其分類,然後我們得出來以上三種結果。假設來了第5個點,它其實就是上面4個點中最左邊的那一個點‘ * ’,但是,由於測量等影響,有了一些誤差。作為我們看來,我們肯定是希望把這個點分為‘ * ’。如果我們用最左邊的那個模型,可以發現,哪怕是一點點的誤差,資料有一點點的干擾,第5個點就有可能被分為 ‘ 。’.再看最右邊的那個模型,發現陰影圓部分都是第5個點可以容忍的誤差範圍。所以,我們認為,資料點離分隔線的距離越大,模型就可以容忍各大的干擾,對過擬合有更好的健壯性。 又點是不能動的,分割線是可以動的。再加上分割線必須把所有點都正確分隔。所以以上也可以理解為,分割線距離 最近點 的距離越大,模型就可以容忍各大的干擾,超平面對過擬合有更好的健壯性。 所以,我們說,由於最右邊的分割線距離 最近點 最遠,於是具有最高的健壯性,所以我們選最右邊的點。
所以,我們是要找到最胖的分隔線,這個最胖的意思,就是分隔線距離最近點的距離。然而前提是,這個分割線要把所有點都正確分隔(預設資料是可分的)。所以最終化成求一個目標函式,但有約束條件。
即
為了規範化,我們定義最胖的意思是,最大邊界,即fatness==largest_margin
約束條件——分隔線必須把點都正確分類,即
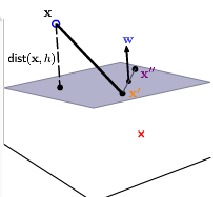
- 為了求出上面方程的解,我們要先弄明白什麼是distance(x,b,w)?
假設超平面的方程為
兩式相減,即可得,
假設平面外有一點 x , 則
這裡h 就是 w
於是可得
好了,我們就表示出了distance(x,b,w)的公式了
由於這是任一點到任意平面的距離公式,然而我們要求的是超平面能夠把所有的資料點正確分類,則有附加條件
其實
即最終化為
我們再來分析分析,我們最終想要的結果是得到超平面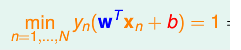
這樣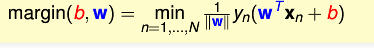
就化簡會
即可得到
由於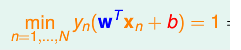
即得到
但是這還是不能求解啊!!約束條件裡面有min。現在就想方法把min也去掉。
對於對上面4點的分隔,如果是用線性迴歸的話,三個圖形都可能發生。因為PLA是遇到一個輸入值,才進行調整,即如果用PLA模型的話,最終的模型與初始狀態和輸入點的順序有關。都是我們從直覺上來看,不難發現,其實最右邊的分割線由於另外兩個分割線的。
那為什麼 tro for eof pen tar nbsp karp none out Ford-Fulkerson方法:dfs實現
dfs 140ms
#include<map>
#include<set>
#include<cmath>
hide ring 拆點 前驅 clas view int for fff 這題看了半天看不懂題意。。。還是看的網上題意寫的
加一個源點一個匯點,把每個點拆成兩個,這兩個點的流量是v,其他聯通的邊都設為無窮大
輸入沒有1的點就與源點連接,輸出只有1的點就與匯點連接
還有這個 href aps flow bit 明顯 log sum dir 一個 題目鏈接:hdu 1565 方格取數(2)
題意:
有一個n*m的方格,每個方格有一個數,現在讓你選一些數。使得和最大。
選的數不能有相鄰的。
題解:
我們知道對於普通二分圖來說,最大獨立點集 + 最小 要求 -c style 相加 宋體 所有 概念 -s 流量 最大流
網絡流的定義:
在一個網絡(有流量)中有兩個特殊的點,一個是網絡的源點(s),流量只出不進,一個是網絡的匯點(t),流量只進不出。
最大 可能 pac 深度優先 bool 技術分享 模擬 機會 r+ ont 網絡流
題記:網絡流是最近講過的最迷算法……
網絡流(network-flows)是一種類比水流的解決問題方法,與線性規劃密切相關。非常重視選手在網絡流上的建模技巧,畫圖是非常關鍵的。
1、最大流 ava clas 最小值 amp get max brush logs ise 給定數組arr和整數num,共返回有多少個子數組滿足 <= num
數組長度N 時間復雜度O(N)
package TT;
import java.util.LinkedL rom lang spa bsp pen from per int eof Every time it rains on Farmer John‘s fields, a pond forms over Bessie‘s favorite clover patch. This queue pre small clu key HA 每一個 void ins 優先隊列(priority queue)是一種用來維護一組數據集合S的數據結構。每一個元素都有一個相關的值,被稱為關鍵字key。
這裏以實現最大優先隊列為例子
最大優先隊列支持的操作如下:INS 結束 last 之一 src typedef 我們 define 是不是 fine 13195的質數因子有5,7,13和29.
600851475143的最大質數因子是多少?
這裏可以肯定的是:1.數字很大,絕對不能暴力。2.如果這是一到OJ題,那麽我們的目的就是盡量縮小這 global log cap {} lse scan bae Go tor 理解處
刷題處
DFS
#include <iostream>
#include <stdio.h>
#include <vector>
#include & 數字 euler class tin urn break 如果 == 素因子
from math import floor
def panduan(num):
if num > 1:
if num > 1:
# 匹配 eof 等於 link 矩陣 class -s esp spa 題意:在一個網格中有若幹個點,每一次可以清除一行或者一列,問最少幾次可以將網格中的點全部清除。
思路:這個題是一個入門的最大匹配題(這個好像不是思路..)。一般的方式就是將 行 看作集合A,列 看作集合B rop create default 數據文件 32位系統 conn dbf ide 剩余空間 /*分為四步 *//*第1步:創建臨時表空間 */create temporary tablespace emaoyi_temp tempfile ‘D:\app\Adminis
本來博主是沒有心情寫這篇部落格了,因為昨天住的地方遭賊了。半夜兩點多,偷開我家窗戶,把博主臥室裡面的玫瑰金給偷走了。當時博主就睡得特別不舒服,半夜醒來就發現手機被偷了。搞得博主後半夜基本沒有睡,萬幸的是,博主的手機開了“查詢iphone”功能,因此開啟了丟失
原題地址:http://acm.hdu.edu.cn/showproblem.php?pid=1231
演算法核心:
動態規劃, 陣列為vec[]vec[],設dp[i]dp[i] 是以vec[i]
最大k乘積問題
問題描述 設I是一個n位十進位制整數。如果將I分割為k段,則可得到k個整數。這k個整數的乘積稱為I的一個k乘積。試設計一個演算法,對於給定的I和k,求出I的最大k乘積。
樣例輸入:
第一組 5 2 12345
第二組 5 3 4 5 6 2
題目描述
有一條河,河中間有一些石頭,已知石頭的數量和相鄰兩塊石頭之間的距離。現在可以移除一些石頭,問最多移除m塊石頭後(首尾兩塊石頭不可以移除),相鄰兩塊石頭之間的距離的最小值最大是多少。
輸入資料
第一行輸入兩個數字,n(2<=n<=1000)為石頭 在一個網路裡 對於S流到T的流量,有很多值。其中這些值的最大值,我們稱為S到T的最大流
(想象成自來水管,S就是水廠,T就是你家,邊就是管子,最大流就是能流到你家水量的最大值)
介紹三個相關的知識點
(1) 容量網路 &nbs
傳送門
題意
現在有 n 顆糖果,要將其分給 m 個小朋友,每個小朋友都有特定的喜好,如果他得到了自己喜歡的糖果,那麼他將增加K的歡樂值,否則就只會增加1的歡樂值。當第 i 個小朋友的歡樂值大於等於Bi時,他才是高興的
問是否存在一種分配方案,使得所
我們現在用反證法證明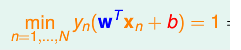
假設二者約束能力不同,即假設相關推薦
svm系列之最大分隔超平面
hdu3549網絡流之最大流
poj3436網絡流之最大流拆點
hdu 1565 方格取數(2)(網絡流之最大點權獨立集)
網絡流之最大流算法
網絡流之最大流
算法總結之 最大值減去最小值或等於num的子數組數量
POJ-1273-Drainage Ditches(網絡流之最大流)
優先隊列(oriority queue)之最大優先隊列的實現
歐拉項目第三題之最大質數因子
網絡流之最大流-Ford-Fullkerson算法 DFS && BFS
project euler之最大的素因子
POJ 3041 Asteroids 二分圖之最大匹配
oracle 創建表空間及oracle 11g表空間之最大最小
貪心演算法之最大的子組合求解
HDU 1231 簡單DP之最大欄位和
動規之最大k乘積問題
列舉演算法之最大值
網路流之最大流 (二)
網路流之最大費用流