Python程式碼實現NIST隨機性測試
阿新 • • 發佈:2019-01-06
最近科研的需要,需要測試二進位制序列的隨機性
找遍所有內網都沒有找到自己合適的程式碼,網上很多都是講解自己怎麼去下載和安裝sts-2.1.2的開發包,於是我也是一開始就入坑了,之前也是寫了一篇比較完整的工具包的下載和安裝的教程,點選開啟連結,但是如果你按照我的安裝步驟的話,成功安裝肯定是沒有問題的,但是你的使用就會出現各種各樣的問題:
比如我在使用的過程中遇到的問題有:首先,就是經常出現UNDERFLOW的情況,這種情況下,一般都是因為資料量不夠大的情況下造成的,所以如果你用過,你就會發現,想要測試15項的內容,大約你需要1GBit,這對於我們正常的情況下,是非常難的,根本達不到這個資料量,沒錯,肯定有的人會說,你可以不測試那麼多的資料量啊 ,你可以測試部分的測試項啊,我也想啊,但是網上根本沒有發現怎麼使用,單獨測試,而不是使用15項
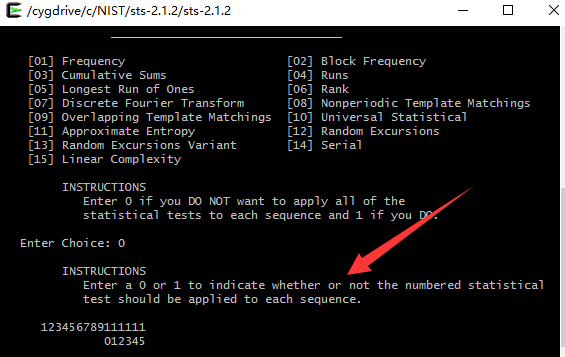
我按照他的步驟,每次單獨測試的時候總是會出現下面的情況,(我不知道你們有沒有遇到)
看這個提示:如果你不想測試所有的項,請輸入0,否則輸入1.
然後我就輸入0
從這裡開始,無論你輸入0還是1,都是沒有響應了。我一直也沒有找到任何解決的辦法,如果有人知道,請留言交流。
但是又因為迫於科研的壓力,還是要解決這個事情,這個是NIST的官方文件
參考開發文件,和國外大牛寫的程式碼:整理並編寫python如下:
這裡把15個測試項都單獨的編寫了一個可以執行的python程式碼:
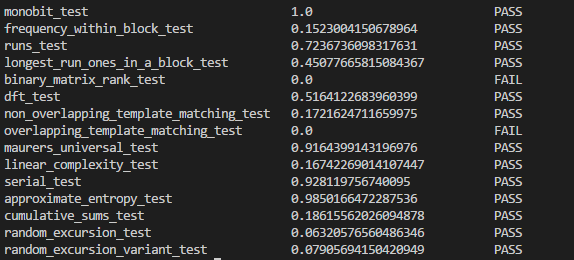
先看一下我的結果圖:有兩項不pass,13項success、
第一個是:
cumulative_sums_test第二個是:maurers_universal_testimport math #from scipy.special import gamma, gammainc, gammaincc from gamma_functions import * #import scipy.stats def normcdf(n): return 0.5 * math.erfc(-n * math.sqrt(0.5)) def p_value(n,z): sum_a = 0.0 startk = int(math.floor((((float(-n)/z)+1.0)/4.0))) endk = int(math.floor((((float(n)/z)-1.0)/4.0))) for k in range(startk,endk+1): c = (((4.0*k)+1.0)*z)/math.sqrt(n) #d = scipy.stats.norm.cdf(c) d = normcdf(c) c = (((4.0*k)-1.0)*z)/math.sqrt(n) #e = scipy.stats.norm.cdf(c) e = normcdf(c) sum_a = sum_a + d - e sum_b = 0.0 startk = int(math.floor((((float(-n)/z)-3.0)/4.0))) endk = int(math.floor((((float(n)/z)-1.0)/4.0))) for k in range(startk,endk+1): c = (((4.0*k)+3.0)*z)/math.sqrt(n) #d = scipy.stats.norm.cdf(c) d = normcdf(c) c = (((4.0*k)+1.0)*z)/math.sqrt(n) #e = scipy.stats.norm.cdf(c) e = normcdf(c) sum_b = sum_b + d - e p = 1.0 - sum_a + sum_b return p def cumulative_sums_test(bits): n = len(bits) # Step 1 x = list() # Convert to +1,-1 for bit in bits: #if bit == 0: x.append((bit*2)-1) # Steps 2 and 3 Combined # Compute the partial sum and records the largest excursion. pos = 0 forward_max = 0 for e in x: pos = pos+e if abs(pos) > forward_max: forward_max = abs(pos) pos = 0 backward_max = 0 for e in reversed(x): pos = pos+e if abs(pos) > backward_max: backward_max = abs(pos) # Step 4 p_forward = p_value(n, forward_max) p_backward = p_value(n,backward_max) success = ((p_forward >= 0.01) and (p_backward >= 0.01)) plist = [p_forward, p_backward] if success: print ("PASS") else: print ("FAIL: Data not random") return (success, None, plist) bits=[1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1,1,1,1, 0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,1,0,1,0, 0,1,1,0,0,0,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,0,0,1,1, 0,0,0,1,1,0,1,0,1,1,1,0,0,1,1,1,1,1,0,0,0] if __name__ == "__main__": #bits = [1,1,0,0,1,0,0,1,0,0,0,0,1,1,1,1,1,1,0,1, # 1,0,1,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0,0,1, #0,1,1,0,1,0,0,0,1,1,0,0,0,0,1,0,0,0,1,1, #0,1,0,0,1,1,0,0,0,1,0,0,1,1,0,0,0,1,1,0, #0,1,1,0,0,0,1,0,1,0,0,0,1,0,1,1,1,0,0,0] success, _, plist = cumulative_sums_test(bits) print ("success =",success) print ("plist = ",plist)
import math def pattern2int(pattern): l = len(pattern) n = 0 for bit in (pattern): n = (n << 1) + bit return n def maurers_universal_test(bits,patternlen=None, initblocks=None): n = len(bits) # Step 1. Choose the block size if patternlen != None: L = patternlen else: ns = [904960,2068480,4654080,10342400, 22753280,49643520,107560960, 231669760,496435200,1059061760] L = 6 if n < 387840: print ("Error. Need at least 387840 bits. Got %d." % n) exit() for threshold in ns: if n >= threshold: L += 1 # Step 2 Split the data into Q and K blocks nblocks = int(math.floor(n/L)) if initblocks != None: Q = initblocks else: Q = 10*(2**L) K = nblocks - Q # Step 3 Construct Table nsymbols = (2**L) T=[0 for x in range(nsymbols)] # zero out the table for i in range(Q): # Mark final position of pattern = bits[i*L:(i+1)*L] # each pattern idx = pattern2int(pattern) T[idx]=i+1 # +1 to number indexes 1..(2**L)+1 # instead of 0..2**L # Step 4 Iterate sum = 0.0 for i in range(Q,nblocks): pattern = bits[i*L:(i+1)*L] j = pattern2int(pattern) dist = i+1-T[j] T[j] = i+1 sum = sum + math.log(dist,2) print (" sum =", sum) # Step 5 Compute the test statistic fn = sum/K print (" fn =",fn) # Step 6 Compute the P Value # Tables from https://static.aminer.org/pdf/PDF/000/120/333/ # a_universal_statistical_test_for_random_bit_generators.pdf ev_table = [0,0.73264948,1.5374383,2.40160681,3.31122472, 4.25342659,5.2177052,6.1962507,7.1836656, 8.1764248,9.1723243,10.170032,11.168765, 12.168070,13.167693,14.167488,15.167379] var_table = [0,0.690,1.338,1.901,2.358,2.705,2.954,3.125, 3.238,3.311,3.356,3.384,3.401,3.410,3.416, 3.419,3.421] # sigma = math.sqrt(var_table[L]) mag = abs((fn - ev_table[L])/((math.sqrt(var_table[L]))*math.sqrt(2))) P = math.erfc(mag) success = (P >= 0.01) return (success, P, None) if __name__ == "__main__": #bits = [0,1,0,1,1,0,1,0,0,1,1,1,0,1,0,1,0,1,1,1] bits=[1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1,1,1,1, 0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,1,0,1,0, 0,1,1,0,0,0,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,0,0,1,1, 0,0,0,1,1,0,1,0,1,1,1,0,0,1,1,1,1,1,0,0,0] success, p, _ = maurers_universal_test(bits, patternlen=2, initblocks=4) print ("success =",success) print ("p = ",p)
這個好沒效率,15項的程式碼太多了,等我把資源上傳到csdn吧,等稽核通過,我再來附連結。