隨機計算(2)——A General Design of Stochastic Circuit and Its Synthesis
1、Abstract
在這篇文章中,為隨機計算電路的設計介紹了一種一般的組合電路設計方法。這種設計方法能夠完成具有任何算術方程功能的電路。
2、Introduction
超大規模積體電路(VLSI circuits)的可靠性成為一個最重要的問題,設計過程存在電壓變化和熱變化引起一系列問題。為此,隨機計算高容錯能力(tolerance of bit-flip errors)能夠很好的解決這些問題。
SC 簡介:它是將數位電路中邏輯域上的運算轉化成概率域上的運算。即:當一個邏輯器件的布林方程是
轉化到概率域上運算就是把每個輸入輸出看作是一個隨機變數,那麼輸出是1的概率是:
例如一個二輸入的AND門,它的布林函式是:
轉化到概率域上運算,要使得輸出隨機變數是1,則輸入變數需要都是1,即:
利用伯努利大數定理可得:一些列獨立同分布的實驗,可以利用頻率去近似概率。所以利用隨機數序列去表示這些概率值,即利用一串二進位制數序列中1出現的頻率去表示這些概率值。如下圖:
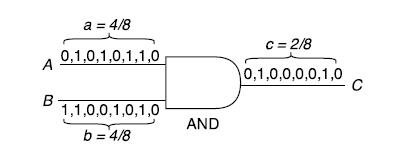
SC一個重要特點就是:它具有強大的容錯能力。
設計SC電路的方法類似於邏輯電路中的設計方法,分為:組合和時序。
這篇文章主要貢獻是:
1、我們為SC引入了一般的組合設計,它只對必要的輸入概率做出假設,而不需要對底層組合電路進行任何額外的假設。 我們分析了隨機域中設計的一般行為。
2、我們提出了一種綜合方法來合成用於實現任意目標算術函式的隨機電路。 我們首先將目標函式轉換為可以通過所提出的設計實現的特殊形式。 但是,布林函式有很多選擇,可以在隨機域中實現轉換後的函式。 我們展示了這些候選布林函式的依據的特徵,並提出了有效的啟發式方法,以確定一個可以減小電路面積和延遲的組合電路的良好選擇。
3、A General Design of Stochastic Design
我們的目的在於設計一個算術函式,即輸出為的概率是。下面我們討論的是組合電路。
首先,這個函式中的變數需要由一系列的輸入提供這些“概率值”(利用RNG產生)。另外這些變數一定會有係數,所以需要額外提供常量輸入,這些常量利用一系列的構成(利用LFSR提供)。因此,文章中提出的設計電路的輸入是:,其中提供一系列的概率值,提供一系列的常量。如下圖:
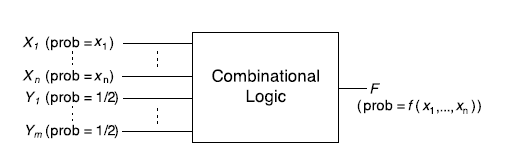
那麼,提出這樣的組合電路到底能夠實現怎麼樣的函式:
