1、Abstract

SC(Stochastic Computing)對於位元翻轉表現出強大的容錯能力(The tolerance to bit-flip errors)。更重要的是，它相比於傳統的二進位制編碼方式計算，能夠利用更簡單的電路實現更復雜的算術功能。在這篇論文中，提出了一種特殊的設計高效能隨機計算電路的方法。這種方法是基於一種啟發式的廣度優點遍歷搜尋演算法在解空間中確定一個最優解進而使得電路滿足一些要求。

2、Introduction

對於SC的基本介紹可以檢視我的這篇部落格：https://blog.csdn.net/qq_34037046/article/details/84306846
中的Introduction

部分，如同其中提到的：我們首先將目標函式轉換為可以通過所提出的設計實現的特殊形式。 但是，布林函式有很多選擇，可以在隨機域中實現轉換後的函式。而這正是隨機計算電路設計的難處，即能夠實現目標函式的解空間是很大的，我們需要找出一個最優的解（即：如何 assign the cubes(product terms)）來滿足一些需求：最低的成本（最少的邏輯閘器件）。但是上面部落格中也提出了一種尋找滿足要求的Cube Assignment方法。即使這種方法很快的確定了解，但是它缺少了在解空間Search的過程，即它無法確定在解空間中到底有沒有比它更優的解。
在這篇論文中，主要的貢獻：
1、提出了一種新的方法利用迭代的方法確定Cube構造目標布林函式；
2、提出了一種啟發式廣度優先遍歷搜尋演算法來尋找更好的Cube 選擇方案；
3、將上述演算法拓展，從而可以應用到多變數多項式中。
這篇文章相對於以前文章中提出的方法主要的改進：
1、提出了廣度優先遍歷演算法，更加節省時間
2、不僅適用於單變數任意多項式，還適用於任意多變數多項式；
3、改進了這個演算法，不僅適用於二級電路，也適用於多級電路。

3、Background on Synthesis Stochastic Circuits

我們提出的方法是基於一個一般形式的隨機電路。
A、一般隨機計算電路和它的表示式
一個一般形式的隨機計算電路如下：

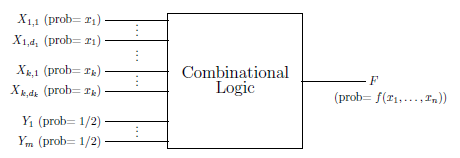
如上圖，可以將輸入分成k+1

個部分。這些個輸入都是相互獨立的。可以注意到第“k+1”個部分的輸入$Y_{1},...,Y_{m}$的所表示的概率值都是$\frac{1}{2}$,這些部分是為了提供多項式的各項係數。在之前的研究中，這些0.5的隨機數由偽隨機位元源產生（例如：LFSR）以及利用另外的附加電路產生別的概率值，例如：比較器。通常將$Y_{1},...,Y_{m}$作為隨機數的輸入，這樣消除了隨機資料路徑和常數概率產生器的界限，也因此有了更大的優化空間（這句話我覺得可以這麼理解：這就像一個齊次線性方程組求解，然後原先這K+1個部分的輸入是完全沒有關聯的，我們可以看成這個向量空間的維度是所有輸入個數的和，然後如果我們選擇將Y部分輸入作為產生X部分的輸入源，那麼就相當於在X與Y之間建立了一種關係，使得矩陣的秩減少，從而解空間的維度增加，使得優化空間更大）。
另外，$m$的選擇很重要。它能夠決定量化誤差的大小，$m$越大，量化誤差越小。這個事先一般會提供需要的精度，這部分見部落格：
https://blog.csdn.net/qq_34037046/article/details/84306846
中的Part4 A有描述。
為了方便描述，接下來做出兩個定義：
$Definition\ 1:\ For\ any\ 0\le s_{1}\le d_{1},...,\ 0\le s_{k}\le d_{k},\\ we\ define\ the\ set:\\ M(s_{1},...,s_{k})=\{a_{1,1},...,a_{1,d_{1}},....,a_{k,1},....,a_{k,d_{k}},b_{1},...,b_{m}\in\{0,1\}^{m+n}\\ ：\sum_{j=1}^{d_{i}}a_{i,j}=s_{i},\ for\ all\ i=1,...,k\}$
$Definition\ 2:\ For\ a\ Boolean\ function\ B,\ its\ on-set,\ denoted\ as\ On(B),\ is\ the\ set\ of\ input\ vectors\ that\ let\ the\ Boolean\ function\ evalute\ to\ 1.$
我們將輸入寫成向量形式：$(a_{1,1},...,a_{k,d_{k}},b_{1},...,b_{m})\in\{0,1\}^{n+m}$，同樣，$(a_{1,1},...,a_{k,d_{k}},b_{1},...,b_{m})\in M(s_{1},...,s_{k})$。任意輸入向量$(X_{1,1},...,X_{k,d_{k}},Y_{1},...,Y_{m})=(a_{1,1},...,a_{k,d_{k}},b_{1},...,b_{m})$的概率是:
$\prod_{i=1}^{k}\prod_{j=1}^{d_{i}}P_{r}(X_{i,j}=a_{i,j}).\prod_{i=1}^{m}P(Y_{i}=b_{i})\\ \Rightarrow\frac{1}{2^{m}}\prod_{i=1}^{k}x_{i}^{s_{i}}(1-x_{i})^{d_{i}-s_{i}}$
根據上面的式子我們可以總結到：在同一個集合$M(s_{1},...,s_{k})$中的任意兩個輸入向量的概率是相等的。換言之，一個$M(s_{1},...,s_{k})$構造了一個等價輸入向量類。這個類中含有的基數是$2^{m}\prod_{i=1}^{k}\binom{d_{i}}{s_{i}}$