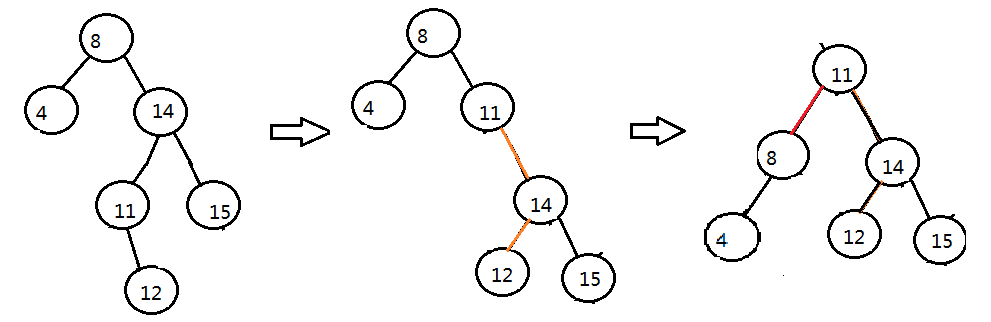
由平衡樹引發的思考
Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
平衡樹的演算法以前研究過,可是因為沒總結這次又忘了,思路往往是一瞬間的,不斷總結還是程式設計師應該養成的一個習慣。
平衡二叉樹是特殊的二叉排序樹,加了一個限定條件:
每個節點的左右子樹不大於1;
二叉排序樹是插入一個節點時,只需要隨意插入即可,隨意性很大,導致極端情況是單支二叉樹。
插入時候的旋轉,分成四種情況:
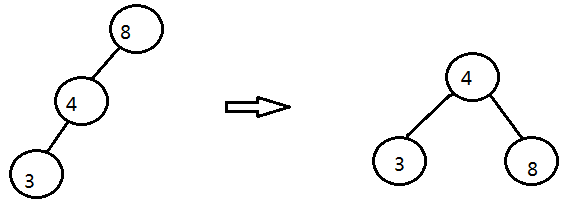
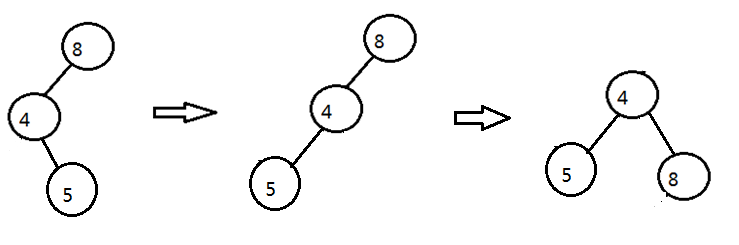
1>左左型:
二叉樹本是 8,4當插入3時
二叉樹情況是,此時我們就應該進行調整,讓其平衡.
我們來看看更復雜的情況:
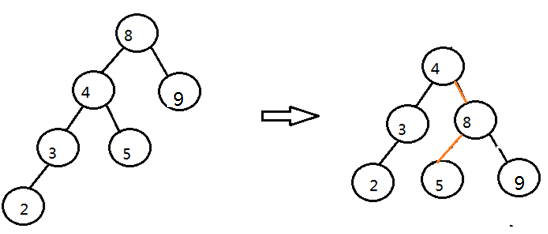
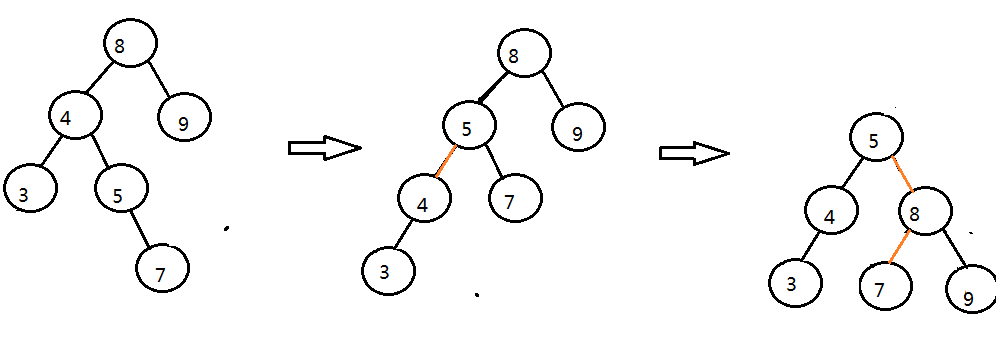
2>左右型
必須先轉換成左左狀態,在按照左左的方法轉化成平衡樹
複雜情況:
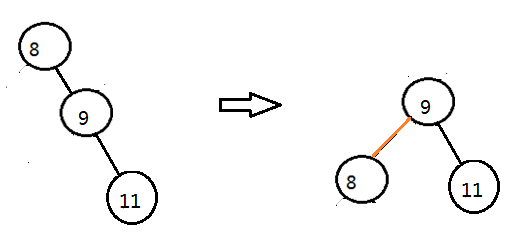
3>右右型
複雜情況:
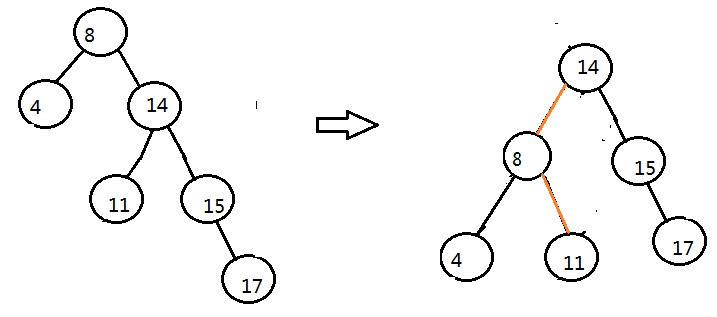
4>右左型
處理方法類似左右
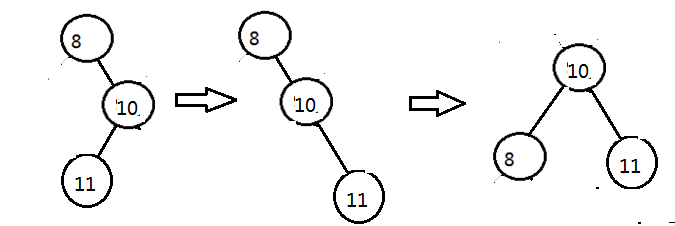
複雜情況:
說是旋轉,其實更多的是換位,比如在左左型情況中,將根節點8拿下來充當4的右子樹,4從而成為新的根節點,而4原來的右子樹變成8的左子樹,調整完後仍符合BST。我們只是將根節點與其中某個節點進行換位,便實現了樹的平衡,在左右和右左兩種情況,我們需要先將其轉化為左左或右右,然後再次呼叫已經實現了的方法即可。
問題是:
將升序的陣列轉化成一顆平衡樹。
完成後搜尋一番,發現我的思路有點複雜,忘記了陣列是有序,
思路:
從第一個開始插入,每插入一個將樹調整為平衡,直到陣列中所有的值已全部插完。
下面貼程式碼:
class Tree { int data; Tree left; Tree right; Tree(int x) { data = x; } Tree(){} } class AvlTree { //獲取當前節點在二叉樹中的高度 public static int getHeight(Tree root) { if(root == null) { return 0; } int leftHeight = getHeight(root.left); int rightHeight = getHeight(root.right); if(leftHeight > rightHeight ) { return leftHeight + 1; } else { return rightHeight + 1; } } public static Tree AvlTreeLeftLeft(Tree root) { //左左型 //必須先將根的左子樹儲存起來,否則根直接換位,左子樹的地址就會丟失 Tree temp = root.left; root.left = temp.right; temp.right = root; return temp; } public static Tree AvlTreeLeftRight(Tree root) { //左右 //跟圖中的方法一樣,先變成左左,再呼叫左左型的處理方法 Tree temp = root.left; root.left = root.left.right; temp.right = root.left.left; root.left.left = temp; root = AvlTreeLeftLeft(root); return root; } public static Tree AvlTreeRightRight(Tree root) { //右右 Tree temp = root.right; root.right = temp.left; temp.left = root; return temp; } public static Tree AvlTreeRightLeft(Tree root) { //右左 //類似左右型,分為兩步,先變成右右,然後呼叫右右的處理方法 Tree temp = root.right; root.right = temp.left; temp.left = root.right.right; root.right.right = temp; root = AvlTreeRightRight(root); return root; } //插入新節點 public static Tree insertNode(int data , Tree root) { if(root == null)//如果當前節點不存在,則分配節點 { root = new Tree(data); root.left = root.right = null; } else if(data<root.data)//小於根節點的權值,往左子樹走 { //直到走到最後的左子樹 root.left = insertNode(data,root.left); //左子樹的高度和右子樹的高度如果等於2,就說明當前BST不平衡,需要調整 if(getHeight(root.left) - getHeight(root.right) == 2) { //左左 if(data < root.left.data)//如果值小於左子樹的值,也就說插入了左子樹的左邊,即左左型 root = AvlTreeLeftLeft(root); else //左右 root = AvlTreeLeftRight(root);//相反是插入到左子樹的右邊 } } else if(data >root.data) //大於,往右子樹走 { root.right = insertNode(data,root.right); if(getHeight(root.right) - getHeight(root.left) == 2) { if(data > root.right.data) //右右 root = AvlTreeRightRight(root); else //右左 root = AvlTreeRightLeft(root); } } return root; } //先序遍歷 public static void prePrint(Tree root) { if(root!=null) { System.out.print(root.data); prePrint(root.left); prePrint(root.right); } } //中序遍歷 public static void InorderPrint(Tree root) { if(root!=null) { InorderPrint(root.left); System.out.print(root.data); InorderPrint(root.right); } } public static void main(String[] args) { int[] num = {1,2,3,4,5,6,7,8}; Tree root = null; for(int i = 0; i<num.length ;i++) { root = insertNode(num[i],root); } //我們利用先序遍歷和中序遍歷可以確定一顆唯一的BST prePrint(root); System.out.println(); InorderPrint(root); } }
完成後我們發現右右型,右左型其實完全就是左左型,左右型的一個映象,只是進行了相反的操作。
提交到Leetcode上結果正確,但是時間超長,覺得應該有更好的方法,然後,傻眼了
其實我們完全可以利用陣列升序來處理這件事,每次選擇中間的,對兩側進行遞迴,從而就可以得到一顆平衡樹。
程式碼如下:
class Tree
{
int data;
Tree left;
Tree right;
Tree(int x) { data = x; }
Tree(){}
}
class Soultion
{
public static Tree toBST(num,start,end)
{
if(start > end) return null;
if(start == end)return new Tree(num[start]);
int mid = (start + end)/2;
Tree node = new Tree(num[mid]);
node.left = toBST(num,start,mid-1);
node.right = toBST(num,mid+1.end);
}
public static Tree getBST(int[] num)
{
Tree root = null;
root = toBST(num,0,num,length-1);
return root;
}
}