公理設計-由奇怪海戰引發的軟體設計思考
前幾天看到了一個部落格,推薦了《公理設計》一書,還有其相關的文件以及視訊。簡單瞭解了一下,增深了一些對軟體設計的理解,特此也推薦給大家。
公理設計理論將設計建立在科學公理、定理和推論的基礎上,由麻省理工學院教授 Nam. P. Suh 領導的研究小組於 1978 年提出,適用於各種類別的設計活動。軟體設計當然也屬於一類工程設計過程,下面我們就來看一下兩者的關聯。
奇怪的海戰
首先從1862年11月13日的一場海戰講起。這場海戰“標誌著蒸汽動力鐵甲艦新時代的到來。為了便於理解,我這裡對艦船名稱進行了修改,想了解的朋友可以百度 U.S.S. Monitor battles C.S.S. Virginia.
南方叛軍的大大號戰艦,體型龐大,非常凶悍。已經擊沉了兩艘聯邦軍艦。北方政府軍則只派出小小號,一艘非常小,火力也小多的軍艦。

大大號顧名思義,它船體特別的大,但是都是固定炮塔,兩側和首尾有很多門炮。而小小號雖然小,卻有一個可以旋轉的炮臺。
我們可以理解為一條戰艦需要有兩個基礎功能:調整航行方向和調整炮擊方向。
對於大大號,這兩個功能需求是耦合 couple 的,要改變炮擊方向,就需要將船隻轉向。而對於小小號,這兩個功能需求則是解耦合 decouple 的,航行方向與炮擊方向無關,炮擊方向可以獨立調整。
於是小小號一直儘量守在大大號的射擊死角攻擊,而大大號雖然火力猛烈則必須不斷通過改變航線來調整炮擊方向,於是就不斷繞圈。這兩條船打了4個小時,大大號不得不撤退了,小小號獲得了勝利。
由此可見功能之間的解耦十分重要,它增加了便捷性和靈活性。
工科生最愛的對映矩陣
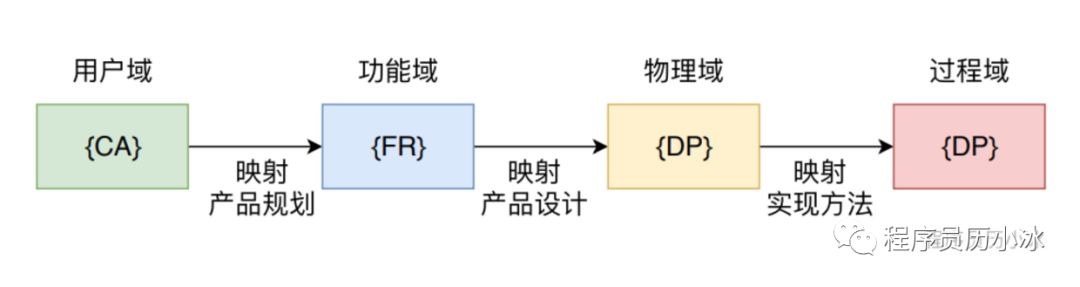
書中由海戰作為引子,介紹了設計過程中的四個域(Domain):
- CNs:Customer Needs,客戶域,就是客戶描述的一大堆自然語言也說不清楚的事情,什麼高階大氣上檔次之類的東西。
- FRs:Functional Requirements,功能域,從 CNs 域到 FRs 域的變換,就是把客戶漫無邊際的需求翻譯成一些可定量的引數,比如戰艦控制系統的 FR 是控制航行方向和控制開炮方向。
- DPs:Design Parameters,設計引數,或者叫物理域,實現 FRs 的物理引數,比如航向控制器和炮塔控制器。
- PVs:Process Variables,過程變數,或者叫過程域,是描述實現功能過程中涉及的過程變數。
相鄰域之間的對映,可以看成目標(做什麼?)和手段(怎樣做?)之間的對應關係。設計過程是相鄰域中特徵向量之間對映和轉換過程。
例如,使用者域元素對映到功能域的過程,實際上是將使用者需求轉變成產品功能要素的過程,即產品規劃;功能域向物理域的對映過程是產品的設計過程;從物理域到過程域的對映則可看成“加工產品”的過程。
其中最為重要的是FRs(功能需求)到DPs(設計引數)的對映,這也是我們軟體開發過程中最長接觸的步驟,需求文件有了,如何進行程式碼設計並實現。

書中以矩陣向量的方式講述了 FRs (功能需求) 和 DPs (設計引數) 的對映關係,也就是上圖中由 A 變數組成的矩陣代表著 FPs 到 DPs 的對映。不同的矩陣代表著不同的對映關係,其實我們不需要關心矩陣各個位置的具體值如何計算,只需簡化的瞭解如果 FP 和 DP 有關聯,則矩陣相應位置上的值為1,否則為0。
比如說小小號上的情況,有兩個功能需要:FR1(調整航向)和FR2(調整開炮方向);以及兩個設計引數:DP1(船舵)和DP2(旋轉炮塔)
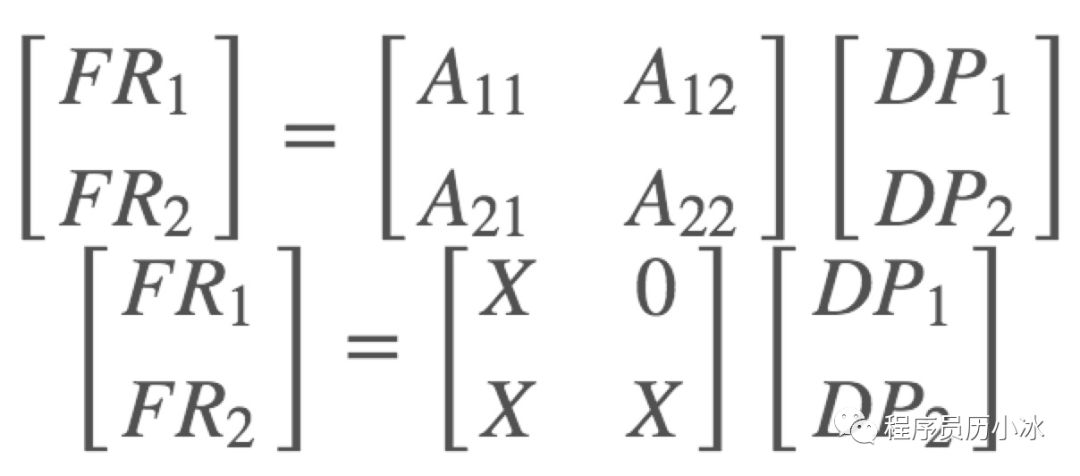
其中轉動船舵的時候,船會轉向,所以A11這裡是X,同時船身上的炮塔也跟著船一起轉向,所以也影響開炮方向FR2,因此A21也是X。 而在旋轉炮塔的時候,不影響船的航行方向,所以A12這裡是0。
好的設計?
所以,基於上邊這個對映矩陣,好的設計應該有兩個特點:
- 首先FRs(功能需求)的數量N,應當等於DPs (設計引數)的數量M。
- 每一個FR(功能需求)與且只與一個DP(設計引數)相互關聯。
也就是說對映矩陣是一個對角矩陣,對角線上有值,其他位置都是0。《程式設計師修煉之道》中也提及了類似的思想,也就是正交性一節。那一節的提示是消除無關事務之間的影響,正好和這裡對映矩陣是對角矩陣不謀而合。當對映舉證是對角矩陣時,說明 FR 和 DP 一一對應,不會有交叉影響。當某一個 FR也就是需求發生變更時,只需要修改一個DP。
當然對角矩陣屬於比較理想的情況,書中也羅列了一些其他型別的對映矩陣。

其中最差的情況是 FRs(功能需求)的數量N,小於 DPs(設計引數)的數量M。也就是大大號中的情景:它有兩個功能需求,FR1 調整航向
和FR2 調整開炮方向,但只有一個DP1 船舵。所以它的對映矩陣如下圖所示。

書中還繼續講解了矩陣分解的知識,也就是對應了需求功能點細分到軟體詳細設計細分等部分的內容,有興趣的小夥伴可以自己去看看。
總結
所以書中最後給出兩個公里:
- 獨立公理(功能獨立性公理)
- 資訊公理(資訊量最少公理)
這不正是軟體設計中經常提及的鬆耦合和高內聚嘛。模組相互獨立互不影響就是鬆耦合,最小化資訊量就是不對外暴露過多資訊,也就是高內聚或者資訊隱藏。
我的部落格,歡迎來玩

