影象的幾何變換：在不改變影象畫素的前提下，對影象畫素進行空間幾何變換。常見的變換：距離變換，座標對映，平移，映象，旋轉，縮放和仿射變換等等。

        影象的幾何變換：建立了一種源影象畫素與變換後的影象畫素之間的對映關係。也正是通過這種對映關係可以知道原影象任意畫素點變換後的座標，或者是變換後的影象在原影象的座標位置等。

一、前向對映

1. 數學公式表示：

表示輸出影象畫素的座標；表示輸入影象的畫素座標；而表示的是兩種對映關係：線性對映或多項式對映；

存在問題：

（1）浮點座標：如（1,1）對映成（0.5,0.5），這是無效座標，這是可以用插演算法進一步處理；

（2）對映不完全：輸入影象的畫素總數小於輸出的畫素總數，會使得輸出影象的部分畫素與原始影象並沒有對映關係，如放大操作；

（3）對映重疊：與對映不完全正好相反，輸出影象會存在對映後的畫素重疊。

2. 前向對映矩陣表示法

其中表示輸出影象畫素的座標，表示輸入影象畫素的座標；

3. 前向對映也稱為素移交對映

輸出影象某一點的畫素值不能直接得到，需要遍歷輸入影象的所有畫素值，對其進行座標變換，分配畫素值到整數位置，才能得到輸出影象各畫素點的畫素值。這是向前對映法的缺點；

二、後向對映

1. 數學公式表示

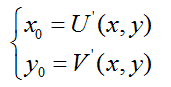
表示輸出影象畫素的座標；表示輸入影象的畫素座標；而

解釋：

（1）與前向對映相反，是由輸出影象的畫素座標反過來推算為該畫素在源影象中的座標位置；

（2）在影象處理中，一般都是用後向對映來實現座標變換的；

（3）前向對映中：適合一些改變影象大小的幾何變換；

（4）後向對映中：適合影象旋轉，不會改變幾何大小。

2. 後向對映矩陣表示法

3. 後向對映也稱為影象填充對映