LIS(最長上升子序列)問題的三種求解方法以及一些例題
摘要
本篇部落格介紹了求LIS的三種方法,分別是O(n^2)的DP,O(nlogn)的二分+貪心法,以及O(nlogn)的樹狀陣列優化的DP,後面給出了5道LIS的例題。
LIS的定義
一個數的序列bi,當b1 < b2 < … < bS的時候,我們稱這個序列是上升的。對於給定的一個序列(a1, a2, …, aN),我們可以得到一些上升的子序列(ai1, ai2, …, aiK),這裡1 <= i1 < i2 < … < iK <= N。比如,對於序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。這些子序列中最長的長度是4,比如子序列(1, 3, 5, 8).
LIS長度的求解方法
解法1:動態規劃
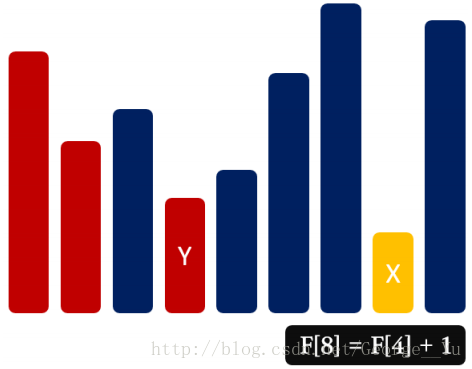
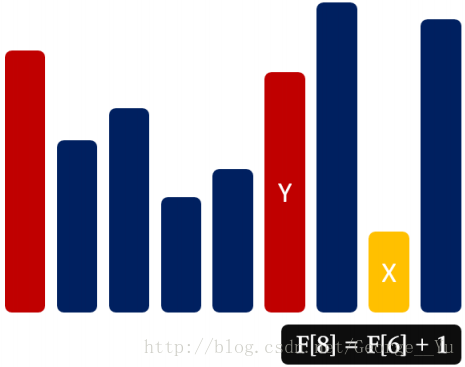
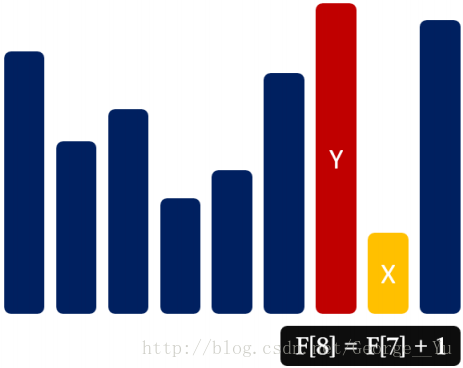
狀態設計:F[i]代表以A[i]結尾的LIS的長度
狀態轉移:F[i]=max{F[j]+1}(1<=j< i,A[j]< A[i])
邊界處理:F[i]=1(1<=i<=n)
時間複雜度:O(n^2)
程式碼:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath> 解法2:貪心+二分
思路:
新建一個low陣列,low[i]表示長度為i的LIS結尾元素的最小值。對於一個上升子序列,顯然其結尾元素越小,越有利於在後面接其他的元素,也就越可能變得更長。因此,我們只需要維護low陣列,對於每一個a[i],如果a[i] > low[當前最長的LIS長度],就把a[i]接到當前最長的LIS後面,即low[++當前最長的LIS長度]=a[i]。
那麼,怎麼維護low陣列呢?
對於每一個a[i],如果a[i]能接到LIS後面,就接上去;否則,就用a[i]取更新low陣列。具體方法是,在low陣列中找到第一個大於等於a[i]的元素low[j],用a[i]去更新low[j]。如果從頭到尾掃一遍low陣列的話,時間複雜度仍是O(n^2)。我們注意到low陣列內部一定是單調不降的,所有我們可以二分low陣列,找出第一個大於等於a[i]的元素。二分一次low陣列的時間複雜度的O(lgn),所以總的時間複雜度是O(nlogn)。
程式碼
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =300003,INF=0x7f7f7f7f;
int low[maxn],a[maxn];
int n,ans;
int binary_search(int *a,int r,int x)
//二分查詢,返回a陣列中第一個>=x的位置
{
int l=1,mid;
while(l<=r)
{
mid=(l+r)>>1;
if(a[mid]<=x)
l=mid+1;
else
r=mid-1;
}
return l;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
low[i]=INF;//由於low中存的是最小值,所以low初始化為INF
}
low[1]=a[1];
ans=1;//初始時LIS長度為1
for(int i=2;i<=n;i++)
{
if(a[i]>=low[ans])//若a[i]>=low[ans],直接把a[i]接到後面
low[++ans]=a[i];
else //否則,找到low中第一個>=a[i]的位置low[j],用a[i]更新low[j]
low[binary_search(low,ans,a[i])]=a[i];
}
printf("%d\n",ans);//輸出答案
return 0;
}解法3:樹狀陣列維護
我們再來回顧O(n^2)DP的狀態轉移方程:F[i]=max{F[j]+1}(1<=j< i,A[j]< A[i])
我們在遞推F陣列的時候,每次都要把F陣列掃一遍求F[j]的最大值,時間開銷比較大。我們可以藉助資料結構來優化這個過程。用樹狀陣列來維護F陣列(據說分塊也是可以的,但是分塊是O(n*sqrt(n))的時間複雜度,不如樹狀陣列跑得快),首先把A陣列從小到大排序,同時把A[i]在排序之前的序號記錄下來。然後從小到大列舉A[i],每次用編號小於等於A[i]編號的元素的LIS長度+1來更新答案,同時把編號小於等於A[i]編號元素的LIS長度+1。因為A陣列已經是有序的,所以可以直接更新。有點繞,具體看程式碼。
程式碼:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =103,INF=0x7f7f7f7f;
struct Node{
int val,num;
}z[maxn];
int T[maxn];
int n;
bool cmp(Node a,Node b)
{
return a.val==b.val?a.num<b.num:a.val<b.val;
}
void modify(int x,int y)//把val[x]替換為val[x]和y中較大的數
{
for(;x<=n;x+=x&(-x)) T[x]=max(T[x],y);
}
int query(int x)//返回val[1]~val[x]中的最大值
{
int res=-INF;
for(;x;x-=x&(-x)) res=max(res,T[x]);
return res;
}
int main()
{
int ans=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&z[i].val);
z[i].num=i;//記住val[i]的編號,有點類似於離散化的處理,但沒有去重
}
sort(z+1,z+n+1,cmp);//以權值為第一關鍵字從小到大排序
for(int i=1;i<=n;i++)//按權值從小到大列舉
{
int maxx=query(z[i].num);//查詢編號小於等於num[i]的LIS最大長度
modify(z[i].num,++maxx);//把長度+1,再去更新前面的LIS長度
ans=max(ans,maxx);//更新答案
}
printf("%d\n",ans);
return 0;
}例題
Tips:例題1、4可以用來測試n^2的演算法,例題2、3、5可以用來測試nlogn的演算法
1.洛谷【p1020】導彈攔截
題目描述
某國為了防禦敵國的導彈襲擊,發展出一種導彈攔截系統。但是這種導彈攔截系統有一個缺陷:雖然它的第一發炮彈能夠到達任意的高度,但是以後每一發炮彈都不能高於前一發的高度。某天,雷達捕捉到敵國的導彈來襲。由於該系統還在試用階段,所以只有一套系統,因此有可能不能攔截所有的導彈。
輸入導彈依次飛來的高度(雷達給出的高度資料是不大於30000的正整數),計算這套系統最多能攔截多少導彈,如果要攔截所有導彈最少要配備多少套這種導彈攔截系統。
輸入輸出格式
輸入格式:
一行,若干個正整數最多100個。
輸出格式:
2行,每行一個整數,第一個數字表示這套系統最多能攔截多少導彈,第二個數字表示如果要攔截所有導彈最少要配備多少套這種導彈攔截系統。
輸入輸出樣例
輸入樣例#1:
389 207 155 300 299 170 158 65
輸出樣例#1:
6
2
題解
程式碼:
#include <iostream>//O(n^2)
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn = 103,INF=0x7f7f7f7f;
int a[maxn],f[maxn];
int n,ans,i,j;
int main()
{
for(n=0;~scanf("%d",&a[n+1]);n++) f[n+1]=1;
for(i=1;i<=n;i++)
for(int j=1;j<i;j++)
if(a[j]>a[i]) f[i]=max(f[i],f[j]+1);
for(i=1,ans=-INF;i<=n;i++) ans=max(ans,f[i]);
printf("%d\n",ans);
for(i=1;i<=n;i++) f[i]=1;
for(i=1;i<=n;i++)
for(j=1;j<i;j++)
if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
for(i=1,ans=-INF;i<=n;i++) ans=max(ans,f[i]);
printf("%d\n",ans);
return 0;
}2.洛谷【p2757】導彈的召喚(資料加強版)
題目描述
同導彈攔截
資料範圍
n<=300000
題解
使用O(nlogn)的演算法求解
程式碼:
#include <iostream>//O(nlogn)
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =300003,INF=0x7f7f7f7f;
int f1[maxn],low1[maxn],f2[maxn],low2[maxn],a[maxn];
int n,ans;
int bs1(int *a,int r,int x)//返回a陣列中第一個小於等於x的位置
{
int l=1,mid;
while(l<=r)
{
mid=(l+r)>>1;
if(a[mid]>=x)
l=mid+1;
else
r=mid-1;
}
return l;
}
int bs2(int *a,int r,int x)//返回a陣列中第一個大於x的位置
{
int l=1,mid;
while(l<=r)
{
mid=(l+r)>>1;
if(a[mid]<x)
l=mid+1;
else
r=mid-1;
}
return l;
}
int main()
{
for(n=0;~scanf("%d",&a[n+1]);n++)
{
f2[n+1]=f1[n+1]=1;
low1[n+1]=-INF;
low2[n+1]=INF;
}
low1[1]=a[1];//low[i]表示長度為i的最長下降子序列末尾的最大值
ans=1;
for(int i=2;i<=n;i++)
{
if(a[i]<=low1[ans]) low1[++ans]=a[i];//如果a[i]比當前最長下降子序列的末尾小,直接接到後面
else low1[bs1(low1,ans,a[i])]=a[i];//否則,在low1陣列中找到第一個小於等於a[i]的位置,用a[i]替換
}
printf("%d\n",ans);
low2[1]=a[1];
ans=1;
for(int i=2;i<=n;i++)
{
if(a[i]>low2[ans]) low2[++ans]=a[i];
else low2[bs2(low2,ans,a[i])]=a[i];
}
printf("%d\n",ans);
return 0;
}3.POJ1631 Bridging signals
題目大意
有p條線路,它們有可能相交。現在讓你去掉一些線路,使得剩下的線不相交且線最多(p<40000)。
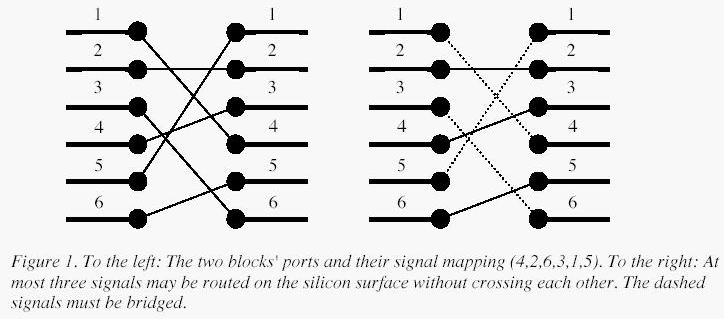
輸入格式:On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.
輸入n個序列,每個序列有p項,每個序列的第i個數ai代表左邊的 i 號接到了右邊的ai號。
題解
對輸入的序列求LIS即可,由於p<40000而且是多組測試資料,要用nlogn的演算法。
4.洛谷【p1091】合唱隊形
題目描述
N位同學站成一排,音樂老師要請其中的(N-K)位同學出列,使得剩下的K位同學排成合唱隊形。
合唱隊形是指這樣的一種隊形:設K位同學從左到右依次編號為1,2…,K,他們的身高分別為T1,T2,…,TK, 則他們的身高滿足T1<…Ti+1>…>TK(1<=i<=K)。
你的任務是,已知所有N位同學的身高,計算最少需要幾位同學出列,可以使得剩下的同學排成合唱隊形。
輸入輸出格式
輸入格式:
輸入檔案chorus.in的第一行是一個整數N(2<=N<=100),表示同學的總數。第一行有n個整數,用空格分隔,第i個整數Ti(130<=Ti<=230)是第i位同學的身高(釐米)。
輸出格式:
輸出檔案chorus.out包括一行,這一行只包含一個整數,就是最少需要幾位同學出列。
輸入輸出樣例
輸入樣例#1:
8
186 186 150 200 160 130 197 220
輸出樣例#1:
4
資料範圍
對於50%的資料,保證有n<=20;
對於全部的資料,保證有n<=100。
題解
合唱隊形要求的是先上升,再下降的最長子序列,如圖:
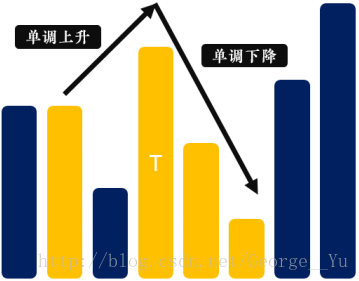
狀態設計:F[i]表示以i結尾的最長上升子序列,G[i]代表從i開始的最長下降子序列。
狀態轉移:F[i]=max{F[j+1]}(1<=j < i,A[j]< A[i]),G[i]=max{G[j]+1}(i< j<=n,A[j]< A[i])
邊界處理:F[i]=1,G[i]=1(1<=i<=n)
最後的答案是ans=max{F[i]+G[i]-1}(1<=i<=n)
減1的原因是i重複算了兩遍
程式碼:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn =1001;
int a[maxn],f[maxn],g[maxn];
int n;
int main()
{
int ans=0,l;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
g[i]=f[i]=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=i-1;j++)
if(a[j]<a[i]&&f[i]<f[j]+1)
f[i]=f[j]+1;
}
for(int i=n;i>=1;i--){
for(int j=n;j>=i+1;j--)
if(a[j]<a[i]&&g[i]<g[j]+1)
g[i]=g[j]+1;
}
for(int i=1;i<=n;i++)
ans=max(ans,f[i]+g[i]-1);
printf("%d\n",n-ans);
return 0;
}5.洛谷【p1439】排列LCS問題
題目描述
給出1-n的兩個排列P1和P2,求它們的最長公共子序列。
輸入輸出格式
輸入格式:
第一行是一個數n,
接下來兩行,每行為n個數,為自然數1-n的一個排列。
輸出格式:
一個數,即最長公共子序列的長度
輸入輸出樣例
輸入樣例#1:
5
3 2 1 4 5
1 2 3 4 5
輸出樣例#1:
3
【資料規模】
對於50%的資料,n≤1000
對於100%的資料,n≤100000
題解
50分做法:直接跑LCS(最長公共子序列)
滿分做法:
注意到題目中的兩個序列都是1~n的一個排列。若其中一個排列是1,2,3…n,那麼他們的LCS(最長公共子序列)就是就是另一個序列的LIS(最長上升子序列)。如果兩個序列的排列都不是1,2,3…n,那麼我們可以認為其中一個序列是1,2,3..n,然後把第一個序列的a[1]對映到1,a[2]對映到2,a[n]對映到n,對b序列也按照a序列的對映規則處理,這樣再求b序列的LIS即可。
程式碼:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =100003,INF=0x7f7f7f7f;
int low[maxn];
int a[maxn],b[maxn];
int main()
{
int n,ans=1;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
a[x]=i;//把a[i]對映到i
}
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
b[i]=a[x];//把b陣列按照a陣列的對映規則進行對映
}
for(int i=1;i<=n;i++) low[i]=INF;//初始化
low[1]=b[1];
for(int i=2;i<=n;i++)
{
if(b[i]>=low[ans])
low[++ans]=b[i];
else
low[lower_bound(low+1,low+ans+1,b[i])-low]=b[i];//利用STL的lower_bound減少碼量
}
printf("%d\n",ans);
return 0;
}後記
本人水平有限,本文如有錯誤,歡迎指正:)