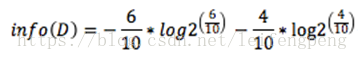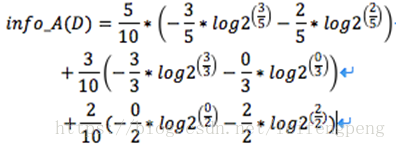DeepLearning基礎學習筆記二(決策樹演算法DecisionTree)
概念
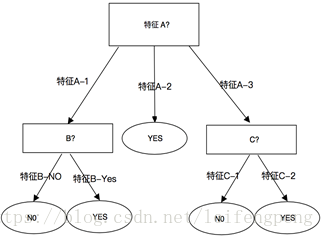
決策樹是一個類似於流程圖的樹結構,可用於資料預測,其中每個內部節點表示在一個屬性上的測試,每個分枝代表一個屬性輸出,而每個樹葉節點代表類或類分佈。樹的最頂層為根結點,結構圖如下:
其中某一個數據實例包含特徵[A,B,C,Boolean],以A為根結點判斷A特徵取值(A-1,A-2,A-3),在特徵A-2中只存在一種情況,因此不需要在分枝決策;在特徵A-1,A-3中還存在一種以上的可能性,因此在以B,C特徵為節點繼續進行判斷,知道判斷特徵的結果只剩下一種。
熵(entropy)
1948年,夏農提出了 ”資訊熵(entropy)“的概念一條資訊的資訊量大小和它的不確定性有直接的關係,要搞清楚一件非常非常不確定的事情,或者是我們一無所知的事情,需要了解大量資訊==>資訊量的度量就等於不確定性的多少。
位元(bit)來衡量資訊的多少
-(p1log(p1)+p2
可寫成函式
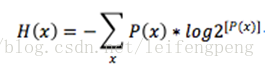
變數的不確定性越大(也就是X值越小),資訊熵也就越大。
如例子:現在有如下資料(根據不同的情況買iphoneX的人進行統計),特徵有“年齡”=[youth,middle_aged,senior],“收入=[high,medium,low]”,“是否學生=[yes,no]”,“信用度=[bad,good]”
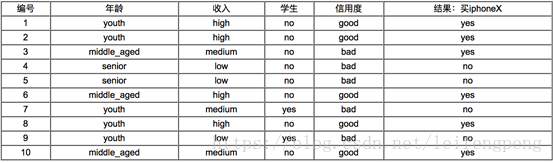
其基本結構圖如下:
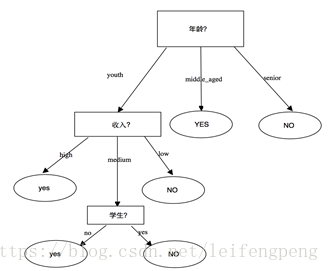
決策樹ID3歸納演算法
在1970-1980, J.Ross. Quinlan, 提出ID3演算法。
如何選擇屬性判斷節點(節點到底以哪個為標準?為什麼以“年齡”,“收入”,“信用度”作為結點):
資訊獲取量(Information Gain)
Gain(A)=info(D)-info_A(D)
計算通過A特徵來作為節點分類獲取了多少資訊
根據以上表格資料,和以上Gain公式可知:
info(D)表示對於目標“買iphoneX”資訊熵,“-6/10log2[(6/10)]”表示買iphoneX的概率,“-4/10log2[(4/10)]”表示不買iphonX概率
對於關於年齡的資訊熵:
備註:
5/10*(-3/5log2[3/5],-2/10log2[2/5])=年輕人在整體例項集佔比 x ( -在年輕人中買手機概率 -不買手機概率)
3/10(-3/3log2[3/3]-0/3log2[0/3])=中年人在整體例項集佔比 x( -在中年人中買手機概率 -不買手機概率)
2/10*(-0/2log2[0/2]-2/2
由上可知 Gain(年齡)=0.940-0.694=0.246 (以年齡分類的資訊獲取量)。
因此以Gain(收入)=0.151,Gain(是否學生)=0.029,Gain(信用度)=0.048可以按照以上分別求出值。
在以上4個特徵中值排序為:Gain(年齡) >Gain(收入)>Gain(信用度)>Gain(是否學生),因此該節點以 “年齡”為標準。
總結歸納
1 .樹代表訓練樣本的單個節點開始.
2 如果樣本在同一個類,則該節點稱為樹葉。
3 如果樣本不在同一個類,則演算法使用資訊增益熵的度量作為評判資訊,選擇能夠最好將樣本分類的屬性
4 所有屬性都是分類的,即是離散值。如果是連續的值必須離散化先(如年齡為具體數字,著需要對數字離散化1-10為一個段,10-100位一個段…)。
5 對測試屬性的每個已知的值,建立一個分枝,並據此劃分樣本。
6 演算法使用同樣過程,遞迴形成每個劃分上的樣本判定。如果以惡屬性出現在一個節點上就不需要在該節點的任何後代考慮(意思是如年齡已經成為一個節點,那麼子節點中不需要考慮“年齡”特徵)
7 遞迴劃分步驟,當只剩下一下條件成立即停止:
7-1 給定節點所有樣本屬於同一類;7-2 沒有剩餘屬性可以用來進一步劃分(使用多數表決)
決策樹優點:
直觀,便於理解,小規模資料有效。
決策樹缺點:
處理連續變數不好,類別較多時錯誤增加快,可規模性一般。