機器學習:向量空間中的投影
阿新 • • 發佈:2019-01-07
今天介紹向量空間中的投影,以及投影矩陣。
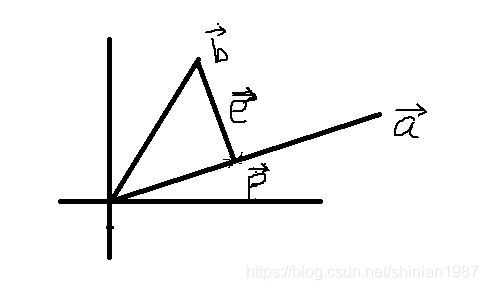
假設空間中有兩個向量 , 在 上的投影為 ,我們要計算出 到底是多少,如下圖所示:
為了計算 ,我們可以先假設 ,因為 是在 上,所以兩者只差係數的關係,如上圖所示,我們可以找到 和 的差:,而我們又可以看出, 是和 垂直的,所以 ,我們可以進一步得到,
所以:
進而:
所以:
所以投影矩陣
這是到直線的投影,如果是到矩陣的投影,我們也可以用類似的方法求得, 只是將上面的向量 換成矩陣 ,假設向量 在矩陣 上的投影為 ,相當於向量 投影到了矩陣 的列空間上,而矩陣 的列空間與其 left-null 空間是互相垂直的,所以:
所以:
進而:
所以:
所以投影矩陣
關於投影,最後多說幾句,講講點到直線的距離,這個與機器學習中的 SVM 的最初的優化函式有關:
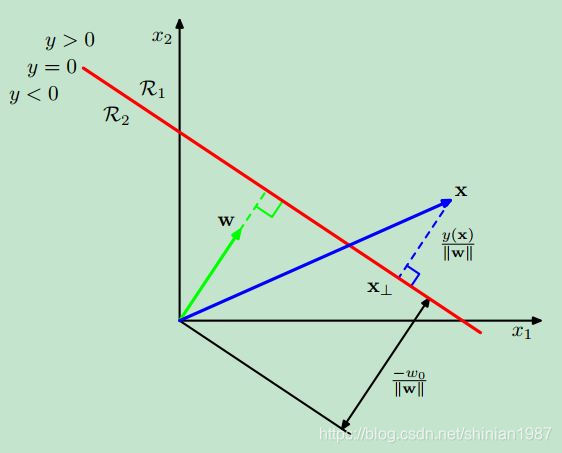
這個圖是那本經典的機器學習教材 《Pattern Recognition and Machine Learning》裡的,這個是想說明向量空間中,一個點到直線的距離。假設直線的表示式為 ,如果我們要求一個點 到該直線的距離,我們可以用上面說的投影來求這個距離, 假設點 到直線上的投影為 ,如上圖的 ,而 到 的這個向量與 是平行的,所以我們可以得到如下的表示式:
兩邊同時乘以 並且加上 , 可以得到:
因為 在直線上,所以 ,進而,我們可以得到:
因為 是單位向量,所以這個向量的幅值就是 ,所以點 到該直線的距離就是 。這個距離的表示式,就是機器學習裡 SVM 的基礎,SVM 要優化的就是尋找這樣一個 使得所有離該直線最近的點的距離最遠,聽起來好像有點繞哈~