有理數類的定義與實現
阿新 • • 發佈:2019-01-07
一個有理數是由一個分子和分母組成的a/b形式的數。我們知道一般程式語言裡已經定義了整形類,浮點型,字元型,但並不支援有理數型。這對於分數的精確計算如1/3=0.33333....不能用double 或者float精確表示,所以有必要自己定義一個有理數類Rational類:
含有分子nume和分母deno兩個資料域;
可以進行加減乘除比較,轉換等多種函式
定義的類如下:
int gys(int x,int y){ x=abs(x); y=abs(y); int t=1; int f=1; while(t<=x&&t<=y){ int re1=x%t; int re2=y%t; if(re1==0&&re2==0) f=t; t++;} return f;}//求得最大公約數 int gbs(int x,int y){ x=abs(x); y=abs(y); int f=1; int t=x*y; while(t>=x&&t>=y){ int re1=t%x; int re2=t%y; if(re1==0&&re2==0) f=t; t--;} return f;}//求得最小公倍數 class Rational{ private: long nume; long deno; public: Rational(){nume=0;deno=1;} Rational(long nume,long b){this->nume=nume;deno=b;} long getnume(){return nume;} long getdeno(){return deno;} Rational getadd(Rational &s){ int deno1=gbs(deno,s.getdeno()); int fnume1=deno1/deno; int fnume2=deno1/s.getdeno(); int nume1=fnume1*nume+fnume2*s.getnume(); int gbs=gys(deno1,nume1); int nume2=nume1/gbs; int deno2=deno1/gbs; Rational add(nume2,deno2); return add;}//有理數加法,按照四則運算分數相加法則 Rational getsub(Rational &s){ int deno1=gbs(deno,s.getdeno()); int fnume1=deno1/deno; int fnume2=deno1/s.getdeno(); int nume1=fnume1*nume-fnume2*s.getnume(); int gbs=gys(deno1,nume1); int nume2=nume1/gbs; int deno2=deno1/gbs; Rational sub(nume2,deno2); return sub;}//有理數減法,按照四則運算分數相減法則 Rational getmin(Rational &s){ int nume1=nume*s.getnume(); int deno1=deno*s.getdeno(); int gys1=gys(nume1,deno1); int nume2=nume1/gys1; int deno2=deno1/gys1; Rational sub(nume2,deno2); return sub;}//有理數乘法,直接對應相乘,然後化簡 Rational getdiv(Rational &s){ int snume=s.getdeno(); int sdeno=s.getnume(); Rational s1(snume,sdeno); return getmin(s1);}//有理數除法,除數倒置以後的乘法 int com( Rational &s){ int deno1=gbs(deno,s.getdeno()); int fnume1=deno1/deno; int fnume2=deno1/s.getdeno(); int nume1=fnume1*nume; int nume2=fnume2*s.getnume(); if(nume1>nume2) return 1; else if(nume1==nume2) return 0; else return -1;}//有理數比較,先雷同有理數加減,化成分母相同,直接比較分子即可 bool equ(Rational &s){ if(com(s)==0) return true; else return false;}//直接利用已有的比較函式 int intval(){ return nume/deno;} double doubleval(){ return 1.0*nume/deno;} string tostring(){ char *str=new char[22]; char *str1=new char[22]; if(deno==1) {itoa(nume,str,10);return str;} else {itoa(nume,str,10);itoa(deno,str1,10); string s1(str); string s2(str1); s1.append(1,'/'); s1.append(s2); return s1;}}//涉及到數和字串轉換itoa(),涉及到字串到string 轉換 private: long gcd(long x,long y){ x=abs(x); y=abs(y); long t=1; long f=1; while(t<=x&&t<=y){ int re1=x%t; int re2=y%t; if(re1==0&&re2==0) f=t; t++;} return f;}//求n,d的公約數 };
呼叫:
inline void dis(Rational &s){ cout<<"result:"<<s.getnume()<<"/"<<s.getdeno()<<endl;} int main(){ int a=37,b=10; Rational a1(2,6); //cout<<"enter two:"<<endl; //cin>>a>>b; Rational b1(a,b); Rational add=a1.getadd(b1); dis(add); Rational sub=a1.getsub(b1); dis(sub); Rational min=a1.getmin(b1); dis(min); Rational div=a1.getdiv(b1); dis(div); cout<<a1.com(b1)<<endl; cout<<a1.equ(b1)<<endl; cout<<a1.tostring()<<endl; system("pause"); return 0;}
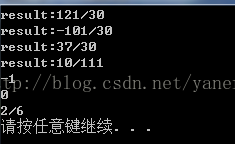
實現結果如圖:
這樣以後不僅僅有int,float,double等資料類,還有有理數類參與計算了。