題目如下：

給出一個可能包含重複的整數陣列，和一個大小為 k 的滑動視窗, 從左到右在陣列中滑動這個視窗，找到陣列中每個視窗內的最大值。O(n)時間，O(k)的額外空間

樣例

給出陣列 [1,2,7,7,8], 滑動視窗大小為 k = 3. 返回 [7,7,8].

解釋：

最開始，視窗的狀態如下：

[|1, 2 ,7| ,7 , 8], 最大值為 7;

然後視窗向右移動一位：

[1, |2, 7, 7|, 8], 最大值為 7;

最後視窗再向右移動一位：

[1, 2, |7, 7, 8|], 最大值為 8.

解題思路：

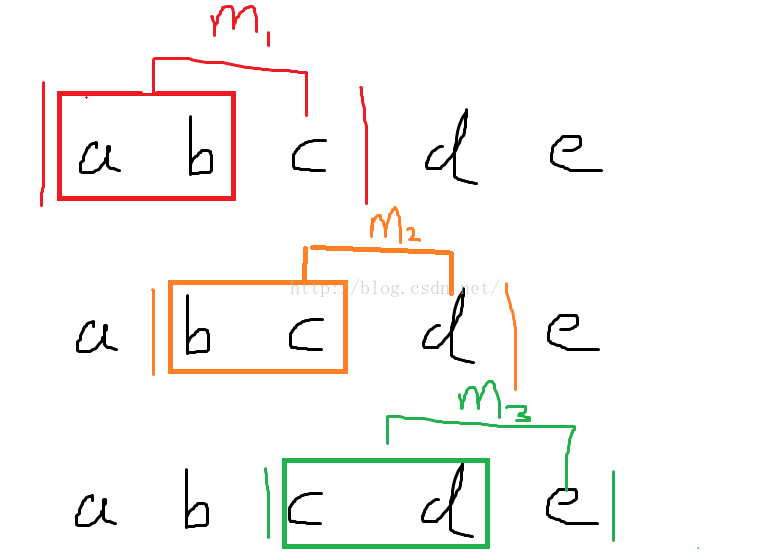
O（n）的複雜度明顯需要快取，每個視窗間都存在並集部分，那麼並集部分的最大值當然就是快取了。至於遍歷，我們可以像下圖一樣（m1，m2，m3為所在視窗最大值

由於我們需要的只是快取裡的最大值，只要在保證快取的最大值在視窗有效區間內，那麼該最大值也就是該視窗的最大值了。顯然，排序快取是不可靠的提取最大值方法，除開復雜度提升問題不說，快取裡儲存的陣列下標也跟排序不相襯，並且快取裡的非區間最大值也許永遠都用不上，因此，我們採取壓榨區間來提取最大值。採用雙向列表的優勢，不停把最後元素與目前遍歷處理的元素相比較，少於則popback，直到列表back元素大於它，大於則pushback，這樣，我們可以確保，列表任意兩個元素組成的區間內的元素都比這兩個元素要小。只要列表最前元素在區間內，此元素也就是該區間最大值，不在，則下一個元素是最大值。

思路程式碼實現如下：

void Method(int *s,int len,int k)
{
    deque<short>d;int i;
    for(i=0;i<len;++i)
    {
        if(!d.empty()&&d.front()==i-k)
            d.pop_front();
        while(!d.empty()&&d.back()<s[i])
            d.pop_back();
        d.push_back(i);
        if(i>=k-1)
            printf("%d ",s[d.front()]);
    }
}