Dijkstra迪傑斯特拉 演算法詳細步驟及實現
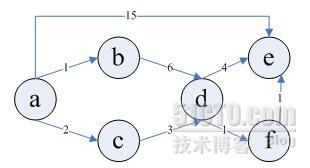
(2)演算法詳細步驟如下表:
| 步驟 | S集合中 | U集合中 |
| 初始化 | 選入a,此時s={a} 此時最短路徑有a->a=0 以a為中間點,從a開始找 | U={b,c,d,e,f} a->b=1 a->c=2 a->e=15 a->其他U中頂點為無窮 |
| 1 | 從U={b,c,d,e,f}中發現路徑a->b=1最短 選入b,S={a,b} 此時最短路徑有a->a=0,a->b=1 以b為中間點,從a->b=1這條最短路徑開始找 | U={c,d,e,f} (a->b->d=7)<初始的無窮 改寫a->b->d=無窮為當前的a->b->d=7 a-> b->其他U中頂點為無窮 |
| 2 | 從U={c,d,e,f}中發現路徑a->c=2最短 選入c,S={a,b,c} 此時最短路徑有 a->a=0,a->b=1,a->c=2 以b為中間點,從a->c=2這條最短路徑開始找 | U={d,e,f} (a->c->d=5)<已有的7 改寫為a->c->d=5 |
| 3 | 從U={d,e,f}中發現路徑a->c->d=5最短 選入d,S={a,b,c,d} 此時最短路徑有 a->a=0,a->b=1,a->c=2,a->c->d=5 以d為中間點,從a->c->d=5這條最短路徑開始找 | U={e,f} (a->c->d->e=9)<步驟1中的15 改寫為a->c->d->e=9 (a->c->d->f=6)<初始的無窮 改寫為a->c->d->f=6 |
| 4 | 從U={e,f}中發現路徑a->c->d->f=6最短 選入f,S={a,b,c,d,f} 此時最短路徑有 a->a=0,a->b=1,a->c=2,a->c->d=5 a->c->d->f=6 以f為中間點,從a->c->d->f=6這條最短路徑開始找 | U={e} (a->c->d->f->e=7)<步驟3中改寫成的9 改寫為a->c->d->f->e=7 |
| 5 | 從U={f}中發現路徑a->c->d->f->e=7最短 選入f,S={a,b,c,d,f,e} 此時最短路徑有 a->a=0,a->b=1,a->c=2,a->c->d=5 a->c->d->f=6,a->c->d->f->e=7 | U集合已空,查詢完畢。 |
例如,對下圖中的有向圖,應用Dijkstra演算法計算從源頂點1到其它頂點間最短路徑的過程列在下表中。

主題好好理解上圖!
以下是具體的實現(C/C++):
#include <iostream>usingnamespace std;
constint maxnum =100;
constint maxint =999999;
void Dijkstra(int n, int v, int*dist, int*prev, int c[maxnum][maxnum])
{
bool s[maxnum]; // 判斷是否已存入該點到S集合中for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i]; //初始化其他點到源點的最短距離
s[i] =0; // 初始都未用過該點if(dist[i] == maxint)//初始化其他點距離源點最短路徑的 前一個點
prev[i] =0; //其他點到源點 不存在路徑時,
else
prev[i] = v;
} //初始化源點的狀態
dist[v] =0;
s[v] =1;
// 依次將未放入S集合的結點中,取dist[]最小值的結點,放入結合S中
// 一旦S包含了所有V中頂點,dist就記錄了從源點到所有其他頂點之間的最短路徑長度for(int i=2; i<=n; ++i)
{
int tmp = maxint;
int u = v;
// 找出當前未使用的點j的dist[j]最小值for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u儲存當前鄰接點中距離最小的點的號碼 tmp = dist[j];
}
s[u] =1; // 表示u點已存入S集合中
// 更新其他點距離源點 最短距離點的 distfor(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<maxint)
{
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
void searchPath(int*prev,int v, int u)
{
int que[maxnum];
int tot =1;
que[tot] = u;
tot++;
int tmp = prev[u];
while(tmp != v)
{
que[tot] = tmp;
tot++;
tmp = prev[tmp];
}
que[tot] = v;
for(int i=tot; i>=1; --i)
if(i !=1)
cout << que[i] <<" -> ";
else
cout << que[i] << endl;
}
int main()
{
freopen("input.txt", "r", stdin);
// 各陣列都從下標1開始int dist[maxnum]; // 表示當前點到源點的最短路徑長度int prev[maxnum]; // 記錄當前點的前一個結點int c[maxnum][maxnum]; // 記錄圖的兩點間路徑長度int n, line; // 圖的結點數和路徑數
// 輸入結點數 cin >> n;
// 輸入路徑數 cin >> line;
int p, q, len; // 輸入p, q兩點及其路徑長度
// 初始化c[][]為maxintfor(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
c[i][j] = maxint;
for(int i=1; i<=line; ++i)
{
cin >> p >> q >> len;
if(len < c[p][q]) // 有重邊 {
c[p][q] = len; // p指向q c[q][p] = len; // q指向p,這樣表示無向圖 }
}
for(int i=1; i<=n; ++i)
dist[i] = maxint;
for(int i=1; i<=n; ++i)
{
for(int j=1; j<=n; ++j)
printf("%8d", c[i][j]);
printf("\n");
}
Dijkstra(n, 1, dist, prev, c);
// 最短路徑長度 cout <<"源點到最後一個頂點的最短路徑長度: "<< dist[n] << endl;
// 路徑 cout <<"源點到最後一個頂點的路徑為: ";
searchPath(prev, 1, n);
}
輸入資料:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
輸出資料:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源點到最後一個頂點的最短路徑長度: 60
源點到最後一個頂點的路徑為: 1 -> 4 -> 3 -> 5
以下是java實現
import java.util.ArrayList;
import java.util.LinkedHashMap;
public class DijkstraPath {
/**
* @param args
*/
static int[][] cost;
static ArrayList<String> visited = new ArrayList<String>();
static ArrayList<String> unVisited = new ArrayList<String>();
static ArrayList<String> vertexs = new ArrayList<String>();
static LinkedHashMap<String ,Integer> shortPath = new LinkedHashMap<String ,Integer>();
static ArrayList<arc> arcs = new ArrayList<arc>();
static LinkedHashMap<String ,String> shortPathWay = new LinkedHashMap<String ,String>();
public static void main(String[] args) {
// TODO Auto-generated method stub
//init the verges set
arcs.add(new arc("A","B",2));
arcs.add(new arc("A","C",4));
arcs.add(new arc("A","D",15));
arcs.add(new arc("B","D",5));
arcs.add(new arc("B","C",1));
arcs.add(new arc("C","D",7));
arcs.add(new arc("D","E",4));
//init the nodes set
vertexs.add("A");
vertexs.add("B");
vertexs.add("C");
vertexs.add("D");
vertexs.add("E");
// init the novisited set
visited.add("A");
//init the visited set
unVisited.add("B");
unVisited.add("C");
unVisited.add("D");
unVisited.add("E");
//init the shortPath map
for(String unvisitNode:unVisited)
{
boolean access = false;
for(arc a:arcs)
{
if(a.startNode.equals("A") && a.endNode.equals(unvisitNode))
{
shortPath.put(unvisitNode,a.weight);
access = true;
break;
}
}
if(access == false)
{
shortPath.put(unvisitNode, -1);
}
}
//把第一個臨近節點的前驅找到
initFirstShortPathWay();
while(unVisited.size()>0){
String lastVisitedNode = getLastVisitedNode();
for(String unvisitNode:unVisited)
{
//獲得最後一訪問節點到未訪問節點到距離
int newPath = getWeight(lastVisitedNode,unvisitNode);
if(newPath > 0)
{
//獲得源點到未訪問節點的距離
int oldPath = getOldPath(unvisitNode);
//如果二者都存在話,改變shortPath 的相應值為最小值
if(oldPath > 0)
{
if(oldPath > getOldPath(lastVisitedNode)+newPath){
resetShortPath(unvisitNode,getOldPath(lastVisitedNode)+newPath);
shortPathWay.put(unvisitNode,lastVisitedNode);//後繼——前驅
}
}
//如果原來不可達的話,但是通過中間節點可以到達,那麼同樣要改變shortPath
else
{
resetShortPath(unvisitNode,getOldPath(lastVisitedNode)+newPath);
shortPathWay.put(unvisitNode,lastVisitedNode);
}
}
}
String minNode = getTheMinPathNode();
removeNode(minNode,unVisited);
addNode(minNode,visited);
}
//輸出最終結果
printResult();
}
//初始化第一個 路徑的前驅
public static void initFirstShortPathWay()
{
int min = 500;
String firstNode ="";
for(String vertex:shortPath.keySet())
{
int tem = shortPath.get(vertex);
if(tem > 0){
min = min > tem?tem:min;
}
}
for(String vertex:shortPath.keySet())
{
if(min == shortPath.get(vertex))firstNode = vertex;
}
shortPathWay.put(firstNode,"A");
}
//add a node to the set
public static void addNode(String node,ArrayList<String> set)
{
set.add(node);
}
// remove a node of the set
public static void removeNode(String delNode,ArrayList<String> set){
int index = 0;
for(int i=0;i<set.size();i++)
{
if(delNode.equals(set.get(i)))
{
index = i;
}
}
set.remove(index);
}
//得到未訪問結點中shutPath的最小值的點
public static String getTheMinPathNode()
{
int min = 500; //距離超過500為不可達
String node = "";
for(String unode:unVisited)
{
int tem = shortPath.get(unode);
if(tem>0){
min = min>tem?tem:min;
}
}
for(String unode:unVisited)
{
if(min == shortPath.get(unode))node=unode;
}
return node;
}
//得到源點到未訪問結點的最短距離
public static int getOldPath(String node)
{
if(node.equals("A"))return 0;
return shortPath.get(node);
}
//重新設定 shortPath
public static void resetShortPath(String node,int path)
{
for(String snode:shortPath.keySet())
{
if(snode.equals(node))shortPath.put(snode, path);
}
}
//get the last node of the visited set
public static String getLastVisitedNode()
{
return visited.get(visited.size()-1);
}
// get the weight
public static int getWeight(String startNode, String endNode)
{
int weight=-1;
for(arc a:arcs)
{
if(a.startNode.equals(startNode) && a.endNode.equals(endNode))
{
weight = a.weight;
System.out.println(a.startNode+"-->"+a.endNode+"="+weight);
}
}
return weight;
}
// get the min num
public static void printResult()
{
for(String vertex:shortPath.keySet())
{
System.out.print("從源點A到"+vertex+"的最短路徑為");
printPath(vertex);
System.out.print(vertex);
System.out.print("長度為:"+shortPath.get(vertex));
System.out.println(" ");
}
}
public static void printPath(String vertex)
{
String node = shortPathWay.get(vertex);
if(!node.equals("A"))printPath(node);
System.out.print(node+" ");
}
}
class arc{
String startNode = "";
String endNode = "";
int weight =0;
public arc(String startNode,String endNode,int weight){
this.startNode = startNode;
this.endNode = endNode;
this.weight = weight;
}
}

