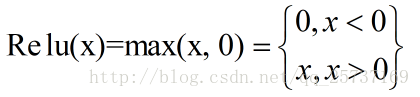前言

本文主要深入介紹深度學習中的梯度消失和梯度爆炸的問題以及解決方案。本文分為三部分，第一部分主要直觀的介紹深度學習中為什麼使用梯度更新，第二部分主要介紹深度學習中梯度消失及爆炸的原因，第三部分對提出梯度消失及爆炸的解決方案。有基礎的同鞋可以跳著閱讀。 
其中，梯度消失爆炸的解決方案主要包括以下幾個部分。

- 預訓練加微調
- 梯度剪下、權重正則（針對梯度爆炸）
- 使用不同的啟用函式
- 使用batchnorm
- 使用殘差結構
- 使用LSTM網路

• 1
• 2
• 3
• 4
• 5
• 6
• 7

第一部分：為什麼要使用梯度更新規則

在介紹梯度消失以及爆炸之前，先簡單說一說梯度消失的根源—–深度神經網路和反向傳播。目前深度學習方法中，深度神經網路的發展造就了我們可以構建更深層的網路完成更復雜的任務，深層網路比如深度卷積網路，LSTM等等，而且最終結果表明，在處理複雜任務上，深度網路比淺層的網路具有更好的效果。但是，目前優化神經網路的方法都是基於反向傳播的思想，即根據損失函式計算的誤差通過梯度反向傳播的方式，指導深度網路權值的更新優化。這樣做是有一定原因的，首先，深層網路由許多非線性層堆疊而來，每一層非線性層都可以視為是一個非線性函式 f(x)f(x)(非線性來自於非線性啟用函式），因此整個深度網路可以視為是一個複合的非線性多元函式 

F(x)=fn(...f3(f2(f1(x)∗θ1+b)∗θ2+b)...)F(x)=fn(...f3(f2(f1(x)∗θ1+b)∗θ2+b)...)

我們最終的目的是希望這個多元函式可以很好的完成輸入到輸出之間的對映，假設不同的輸入，輸出的最優解是g(x)g(x) ，那麼，優化深度網路就是為了尋找到合適的權值，滿足Loss=L(g(x),F(x))Loss=L(g(x),F(x))取得極小值點，比如最簡單的損失函式 

Loss=||g(x)−f(x)||22Loss=||g(x)−f(x)||22

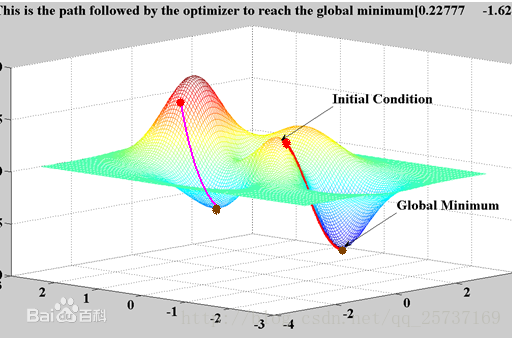
,假設損失函式的資料空間是下圖這樣的，我們最優的權值就是為了尋找下圖中的最小值點，對於這種數學尋找最小值問題，採用梯度下降的方法再適合不過了。 

第二部分：梯度消失、爆炸

梯度消失與梯度爆炸其實是一種情況，看接下來的文章就知道了。兩種情況下梯度消失經常出現，一是在深層網路中，二是採用了不合適的損失函式，比如sigmoid。梯度爆炸一般出現在深層網路和權值初始化值太大的情況下，下面分別從這兩個角度分析梯度消失和爆炸的原因。

1.深層網路角度

比較簡單的深層網路如下：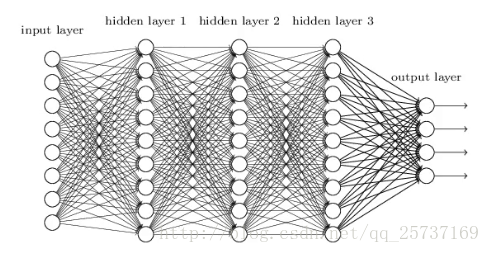 
 
圖中是一個四層的全連線網路，假設每一層網路啟用後的輸出為fi(x)fi(x),其中ii為第ii層, xx代表第ii層的輸入，也就是第i−1i−1層的輸出，ff是啟用函式，那麼，得出fi+1=f(fi∗wi+1+bi+1)fi+1=f(fi∗wi+1+bi+1)，簡單記為fi+1=f(fi∗wi+1)fi+1=f(fi∗wi+1)。 
BP演算法基於梯度下降策略，以目標的負梯度方向對引數進行調整，引數的更新為w←w+Δww←w+Δw，給定學習率αα，得出Δw=−α∂Loss∂wΔw=−α∂Loss∂w。如果要更新第二隱藏層的權值資訊，根據鏈式求導法則，更新梯度資訊： 
Δw1=∂Loss∂w2=∂Loss∂f4∂f4∂f3∂f3∂f2∂f2∂w2Δw1=∂Loss∂w2=∂Loss∂f4∂f4∂f3∂f3∂f2∂f2∂w2，很容易看出來∂f2∂w2=f1∂f2∂w2=f1，即第二隱藏層的輸入。 
所以說，∂f4∂f3∂f4∂f3就是對啟用函式進行求導，如果此部分大於1，那麼層數增多的時候，最終的求出的梯度更新將以指數形式增加，即發生梯度爆炸

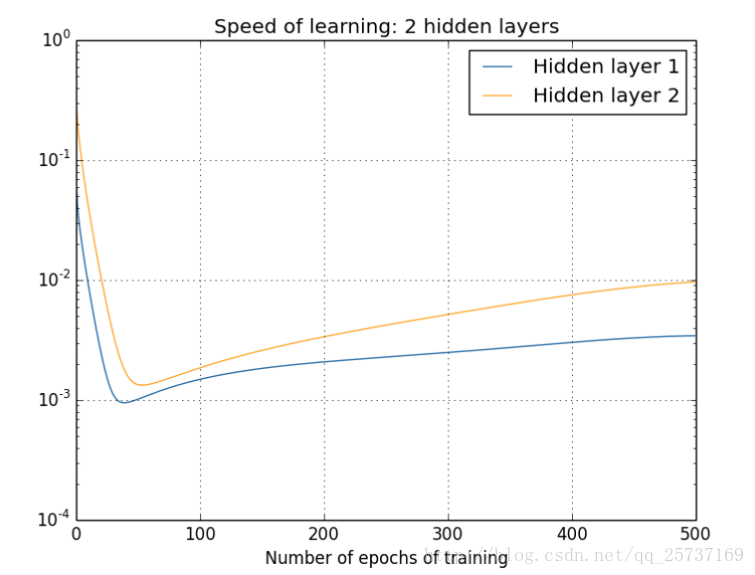
注：下圖中的隱層標號和第一張全連線圖隱層標號剛好相反。 
圖中的曲線表示權值更新的速度，對於下圖兩個隱層的網路來說，已經可以發現隱藏層2的權值更新速度要比隱藏層1更新的速度慢

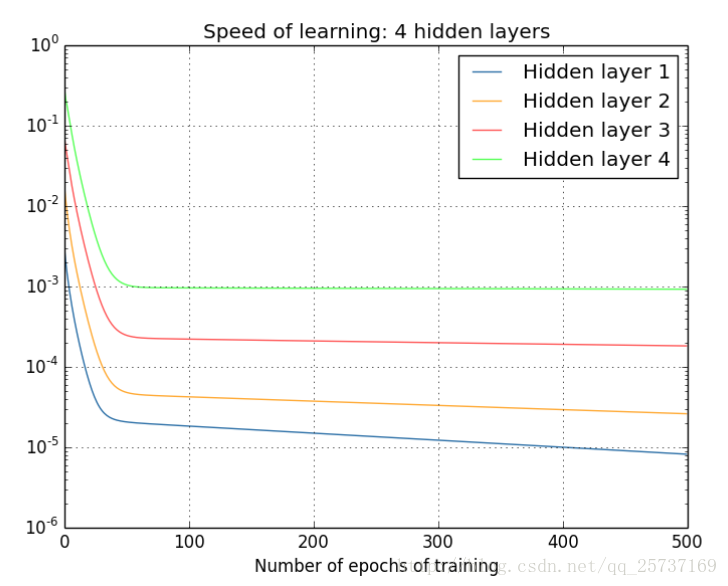
    那麼對於四個隱層的網路來說，就更明顯了，第四隱藏層比第一隱藏層的更新速度慢了兩個數量級：

• 1
• 2

總結：從深層網路角度來講，不同的層學習的速度差異很大，表現為網路中靠近輸出的層學習的情況很好，靠近輸入的層學習的很慢，有時甚至訓練了很久，前幾層的權值和剛開始隨機初始化的值差不多。因此，梯度消失、爆炸，其根本原因在於反向傳播訓練法則，屬於先天不足，另外多說一句，Hinton提出capsule的原因就是為了徹底拋棄反向傳播，如果真能大範圍普及，那真是一個革命。

2.啟用函式角度

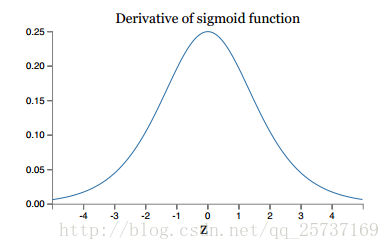
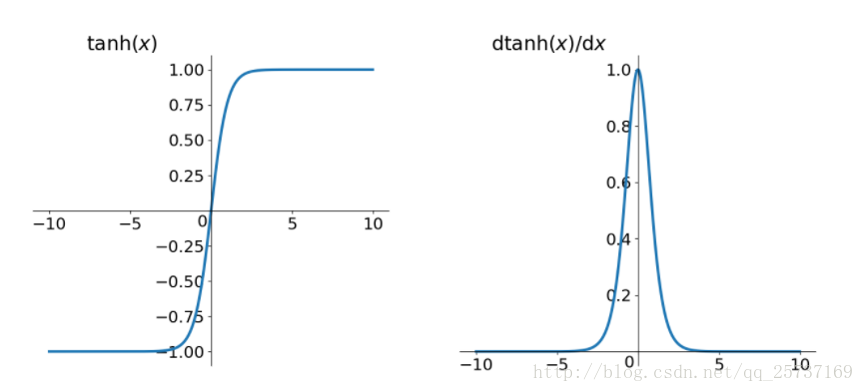
其實也注意到了，上文中提到計算權值更新資訊的時候需要計算前層偏導資訊，因此如果啟用函式選擇不合適，比如使用sigmoid，梯度消失就會很明顯了，原因看下圖，左圖是sigmoid的損失函式圖，右邊是其倒數的影象，如果使用sigmoid作為損失函式，其梯度是不可能超過0.25的，這樣經過鏈式求導之後，很容易發生梯度消失，sigmoid函式數學表示式為：sigmoid(x)=11+e−xsigmoid(x)=11+e−x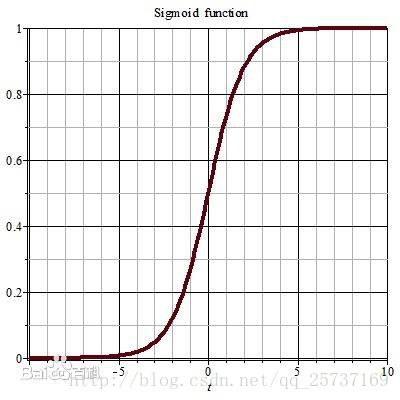 
 

同理，tanh作為啟用函式，它的導數圖如下，可以看出，tanh比sigmoid要好一些，但是它的倒數仍然是小於1的。tanh數學表達為：

• 1
• 2

tanh(x)=ex−e−xex+e−xtanh(x)=ex−e−xex+e−x

第三部分：梯度消失、爆炸的解決方案

2.1 方案1-預訓練加微調

此方法來自Hinton在2006年發表的一篇論文，Hinton為了解決梯度的問題，提出採取無監督逐層訓練方法，其基本思想是每次訓練一層隱節點，訓練時將上一層隱節點的輸出作為輸入，而本層隱節點的輸出作為下一層隱節點的輸入，此過程就是逐層“預訓練”（pre-training）；在預訓練完成後，再對整個網路進行“微調”（fine-tunning）。Hinton在訓練深度信念網路（Deep Belief Networks中，使用了這個方法，在各層預訓練完成後，再利用BP演算法對整個網路進行訓練。此思想相當於是先尋找區域性最優，然後整合起來尋找全域性最優，此方法有一定的好處，但是目前應用的不是很多了。

2.2 方案2-梯度剪下、正則

梯度剪下這個方案主要是針對梯度爆炸提出的，其思想是設定一個梯度剪下閾值，然後更新梯度的時候，如果梯度超過這個閾值，那麼就將其強制限制在這個範圍之內。這可以防止梯度爆炸。

注：在WGAN中也有梯度剪下限制操作，但是和這個是不一樣的，WGAN限制梯度更新資訊是為了保證lipchitz條件。

• 1
• 2

另外一種解決梯度爆炸的手段是採用權重正則化（weithts regularization）比較常見的是l1l1正則，和l2l2正則，在各個深度框架中都有相應的API可以使用正則化，比如在tensorflowtensorflow中，若搭建網路的時候已經設定了正則化引數，則呼叫以下程式碼可以直接計算出正則損失：

regularization_loss = tf.add_n(tf.losses.get_regularization_losses(scope='my_resnet_50'))

• 1

如果沒有設定初始化引數，也可以使用以下程式碼計算l2l2正則損失：

    l2_loss = tf.add_n([tf.nn.l2_loss(var) for var in tf.trainable_variables() if 'weights' in var.name])

• 1
• 2

正則化是通過對網路權重做正則限制過擬合，仔細看正則項在損失函式的形式： 
Loss=(y−WTx)2+α||W||2Loss=(y−WTx)2+α||W||2 
其中，αα是指正則項係數，因此，如果發生梯度爆炸，權值的範數就會變的非常大，通過正則化項，可以部分限制梯度爆炸的發生。

注：事實上，在深度神經網路中，往往是梯度消失出現的更多一些。

• 1
• 2

2.3 方案3-relu、leakrelu、elu等啟用函式

Relu:思想也很簡單，如果啟用函式的導數為1，那麼就不存在梯度消失爆炸的問題了，每層的網路都可以得到相同的更新速度，relu就這樣應運而生。先看一下relu的數學表示式：

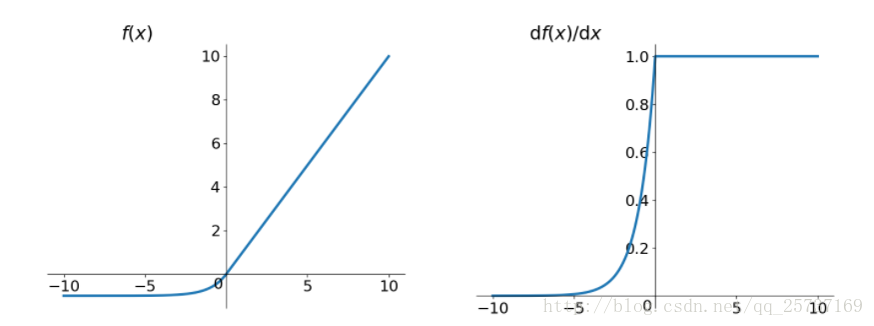
其函式影象：

 
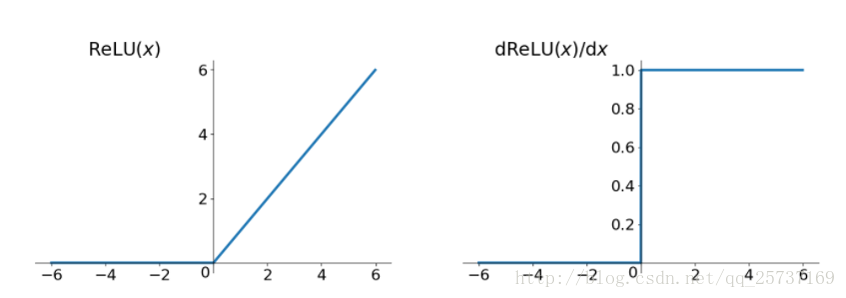
從上圖中，我們可以很容易看出，relu函式的導數在正數部分是恆等於1的，因此在深層網路中使用relu啟用函式就不會導致梯度消失和爆炸的問題。

relu的主要貢獻在於：

 -- 解決了梯度消失、爆炸的問題
 -- 計算方便，計算速度快
 -- 加速了網路的訓練

• 1
• 2
• 3
• 4

同時也存在一些缺點：

-- 由於負數部分恆為0，會導致一些神經元無法啟用（可通過設定小學習率部分解決）
 -- 輸出不是以0為中心的

• 1
• 2
• 3

儘管relu也有缺點，但是仍然是目前使用最多的啟用函式

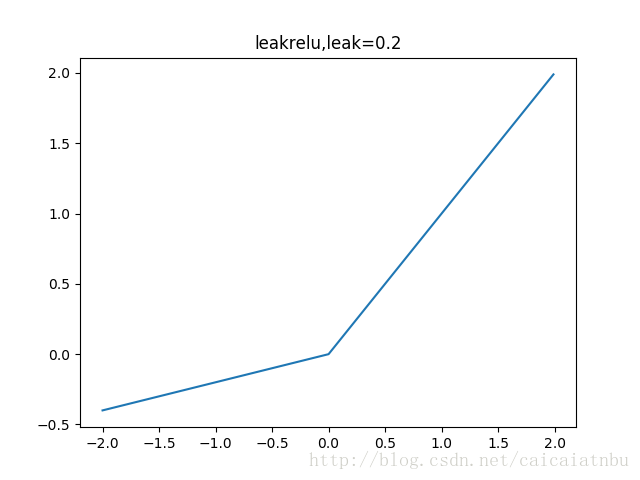
leakrelu 
leakrelu就是為了解決relu的0區間帶來的影響，其數學表達為：leakrelu=max(k∗x,0)leakrelu=max(k∗x,0)其中k是leak係數，一般選擇0.01或者0.02，或者通過學習而來

leakrelu解決了0區間帶來的影響，而且包含了relu的所有優點 
elu 
elu啟用函式也是為了解決relu的0區間帶來的影響，其數學表達為：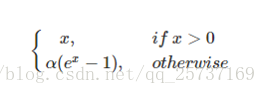 
其函式及其導數數學形式為：

但是elu相對於leakrelu來說，計算要更耗時間一些

2.4 解決方案4-batchnorm

Batchnorm是深度學習發展以來提出的最重要的成果之一了，目前已經被廣泛的應用到了各大網路中，具有加速網路收斂速度，提升訓練穩定性的效果，Batchnorm本質上是解決反向傳播過程中的梯度問題。batchnorm全名是batch normalization，簡稱BN，即批規範化，通過規範化操作將輸出訊號x規範化保證網路的穩定性。 
具體的batchnorm原理非常複雜，在這裡不做詳細展開，此部分大概講一下batchnorm解決梯度的問題上。具體來說就是反向傳播中，經過每一層的梯度會乘以該層的權重，舉個簡單例子： 
正向傳播中f2=f1(wT∗x+b)f2=f1(wT∗x+b)，那麼反向傳播中，∂f2∂x=∂f2∂f1w∂f2∂x=∂f2∂f1w，反向傳播式子中有ww的存在，所以ww的大小影響了梯度的消失和爆炸，batchnorm就是通過對每一層的輸出規範為均值和方差一致的方法，消除了ww帶來的放大縮小的影響，進而解決梯度消失和爆炸的問題，或者可以理解為BN將輸出從飽和區拉倒了非飽和區。 
有關batch norm詳細的內容可以參考我的另一篇部落格： 
http://blog.csdn.net/qq_25737169/article/details/79048516

2.5 解決方案5-殘差結構

殘差結構說起殘差的話，不得不提這篇論文了：Deep Residual Learning for Image Recognition，關於這篇論文的解讀，可以參考知乎連結：https://zhuanlan.zhihu.com/p/31852747這裡只簡單介紹殘差如何解決梯度的問題。 
事實上，就是殘差網路的出現導致了image net比賽的終結，自從殘差提出後，幾乎所有的深度網路都離不開殘差的身影，相比較之前的幾層，幾十層的深度網路，在殘差網路面前都不值一提，殘差可以很輕鬆的構建幾百層，一千多層的網路而不用擔心梯度消失過快的問題，原因就在於殘差的捷徑（shortcut）部分，其中殘差單元如下圖所示：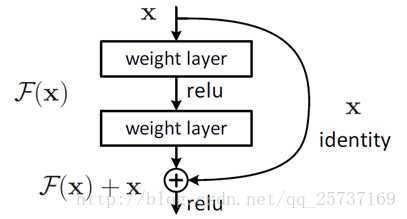 
 
相比較於以前網路的直來直去結構，殘差中有很多這樣的跨層連線結構，這樣的結構在反向傳播中具有很大的好處，見下式： 
 
式子的第一個因子 ∂loss∂xL∂loss∂xL 表示的損失函式到達 L 的梯度，小括號中的1表明短路機制可以無損地傳播梯度，而另外一項殘差梯度則需要經過帶有weights的層，梯度不是直接傳遞過來的。殘差梯度不會那麼巧全為-1，而且就算其比較小，有1的存在也不會導致梯度消失。所以殘差學習會更容易。

注：上面的推導並不是嚴格的證明。

• 1
• 2

2.6 解決方案6-LSTM

LSTM全稱是長短期記憶網路（long-short term memory networks），是不那麼容易發生梯度消失的，主要原因在於LSTM內部複雜的“門”(gates)，如下圖，LSTM通過它內部的“門”可以接下來更新的時候“記住”前幾次訓練的”殘留記憶“，因此，經常用於生成文字中。目前也有基於CNN的LSTM，感興趣的可以嘗試一下。

參考資料: