1、RNN模型結構

　　迴圈神經網路RNN（Recurrent Neural Network）會記憶之前的資訊，並利用之前的資訊影響後面結點的輸出。也就是說，迴圈神經網路的隱藏層之間的結點是有連線的，隱藏層的輸入不僅包括輸入層的輸出，還包括上時刻隱藏層的輸出。下圖為RNN模型結構圖：

2、RNN前向傳播演算法

RNN前向傳播公式為：

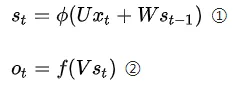
　　其中：

　　　　S_t為t時刻的隱含層狀態值；

　　　　O_t為t時刻的輸出值；

　　　　①是隱含層計算公式，U是輸入x的權重矩陣，S_t-1是t-1時刻的狀態值，W是S_t-1作為輸入的權重矩陣，$\Phi $是啟用函式；

　　　　②是輸出層計算公司，V

　　損失函式（loss function）採用交叉熵$L_{t}=-\overline{o_{t}}logo_{_{t}}$（O_t是t時刻預測輸出，$\overline{o_{t}}$是t時刻正確的輸出） 

那麼對於一次訓練任務中，損失函式$L=\sum_{i=1}^{T}-\overline{o_{t}}logo_{_{t}}$， T是序列總長度。

假設初始狀態S_t為0，t=3 有三段時間序列時，由 ① 帶入②可得到 

　　t1、t2、t3 各個狀態和輸出為：

　　t=1：

　　　　狀態值：$s_{1}=\Phi (Ux_{1}+Ws_{0})$

　　　　輸出：$o_{1}=f(V\Phi (Ux_{1}+Ws_{0}))$

　　t=2：

　　　　狀態值：$s_{2}=\Phi (Ux_{2}+Ws_{1})$

　　　　輸出：$o_{2}=f(V\Phi (Ux_{2}+Ws_{1}))=f(V\Phi (Ux_{2}+W\Phi(Ux_{1}+Ws_{0})))$

　　t=3：

　　　　狀態值：$s_{3}=\Phi (Ux_{3}+Ws_{2})$

　　　　輸出：$o_{3}=f(V\Phi (Ux_{3}+Ws_{2}))=\cdots =f(V\Phi (Ux_{3}+W\Phi(Ux_{2}+W\Phi(Ux_{1}+Ws_{0}))))$

3、RNN反向傳播演算法

　　BPTT（back-propagation through time）演算法是針對循層的訓練演算法，它的基本原理和BP演算法一樣。其演算法本質還是梯度下降法，那麼該演算法的關鍵就是計算各個引數的梯度，對於RNN來說引數有 U、W、V。

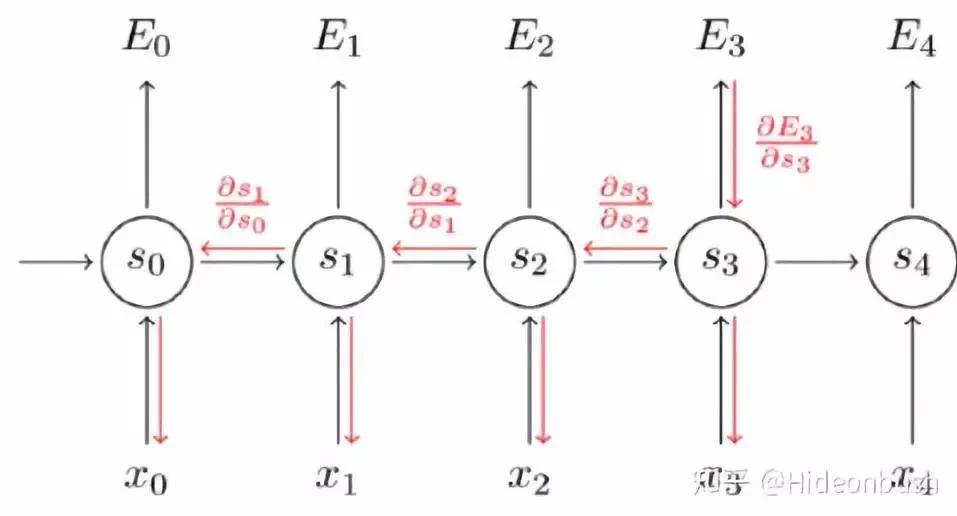
反向傳播 

　　現對t=3時刻的U、W、V求偏導，由鏈式法則得到：

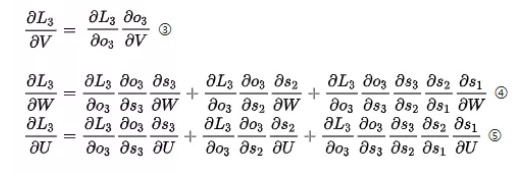
可以簡寫成：

　　觀察③④⑤式，可知，對於 V 求偏導不存在依賴問題；但是對於 W、U 求偏導的時候，由於時間序列長度，存在長期依賴的情況。主要原因可由 t=1、2、3 的情況觀察得 , S_t會隨著時間序列向前傳播，同時S_t是 U、W 的函式。

　　前面得出的求偏導公式⑥，取其中累乘的部分出來，其中啟用函式 Φ 通常是tanh函式 ，則

4、梯度爆炸和梯度消失的原因

　　啟用函式tanh和它的導數影象如下:

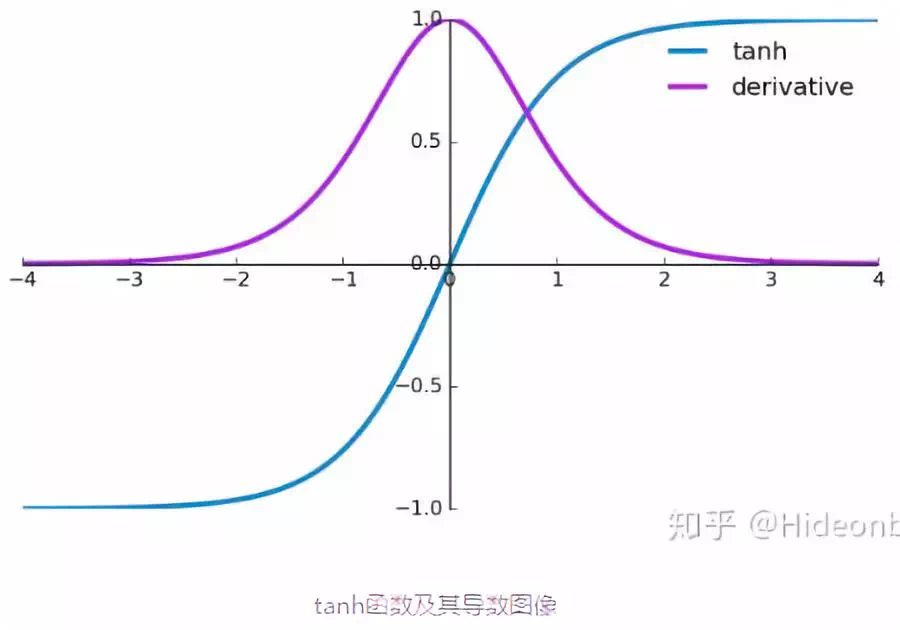
由上圖可知當啟用函式是tanh函式時，tanh函式的導數最大值為1，又不可能一直都取1這種情況，實際上這種情況很少出現，那麼也就是說，大部分都是小於1的數在做累乘，若當t很大的時候，$\prod_{j=k-1}^{t}tan{h}'W$中的$\prod_{j=k-1}^{t}tan{h}'$趨向0，舉個例子：0.8⁵⁰=0.00001427247也已經接近0了，這是RNN中梯度消失的原因。

再看⑦部分：

$\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3}tan{h}'W$

如果引數 W 中的值太大，隨著序列長度同樣存在長期依賴的情況，$\prod_{j=k-1}^{t}tan{h}'W$中的$\prod_{j=k-1}^{t}tan{h}'$趨向於無窮，那麼產生問題就是梯度爆炸。

在平時運用中，RNN比較深，使得梯度爆炸或者梯度消失問題會比較明顯。

5、解決梯度爆炸和梯度消失的方案

1）採使用ReLu啟用函式

　　面對梯度消失問題，可以採用ReLu作為啟用函式，下圖為ReLu函式：

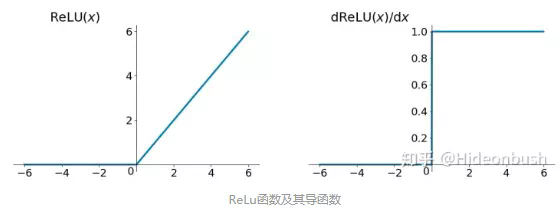
　　ReLU函式在定義域大於0部分的導數恆等於1，這樣可以解決梯度消失的問題，（雖然恆等於1很容易發生梯度爆炸的情況，但可通過設定適當的閾值可解決）。

另外計算方便，計算速度快，可以加速網路訓練。但是，定義域負數部分恆等於零，這樣會造成神經元無法啟用（可通過合理設定學習率，降低發生的概率）。

　　ReLU有優點也有缺點，其中的缺點可以通過其他操作取避免或者減低發生的概率，是目前使用最多的啟用函式。

還可以通過更改內部結構來解決梯度消失和梯度爆炸問題，那就是LSTM了。

2）使用長短記憶網路LSTM

　　使用長短期記憶（LSTM）單元和相關的門型別神經元結構可以減少梯度爆炸和梯度消失問題，LSTM的經典圖為：

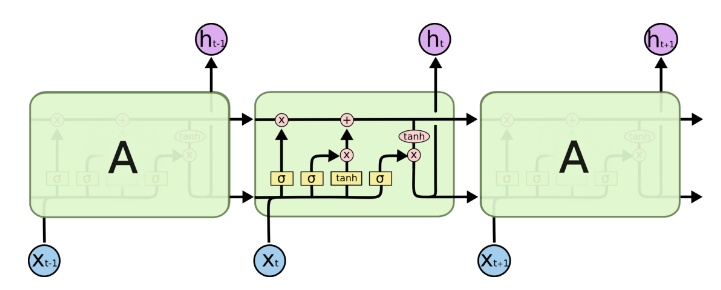
可以抽象為：

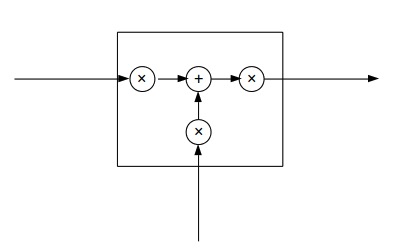
　　三個×分別代表的就是forget gate，input gate，output gate，而我認為LSTM最關鍵的就是forget gate這個部件。這三個gate是如何控制流入流出的呢，其實就是通過下面 _ft，it，ot 三個函式來控制，因為$\sigma (x)$代表sigmoid函式） 的值是介於0到1之間的，剛好用趨近於0時表示流入不能通過gate，趨近於1時表示流入可以通過gate。

$f_{t}=\sigma (W_{f}X_{t}+b_{f})$

$i_{t}=\sigma (W_{i}X_{t}+b_{i)$

$o_{t}=\sigma (W_{o}X_{t}+b_{o})$

　　LSTM當前的狀態值為： $S_{t}=f_{t}S_{t-1}+i_{t}X_{t}$，表示式展開後得：

$S_{t}=\sigma (W_{f}X_{t}+b_{f})S_{t-1}+\sigma (W_{i}X_{t}+b_{i})X_{t}$

　　如果加上啟用函式:

$S_{t}=tanh[\sigma (W_{f}X_{t}+b_{f})S_{t-1}+\sigma (W_{i}X_{t}+b_{i})X_{t}]$

　　上文中講到傳統RNN求偏導的過程包含：

$\prod_{j=k-1}^{t}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{t}tan{h}'W$ 

　　對於LSTM同樣也包含這樣的一項，但是在LSTM中 為：

$\prod_{j=k-1}^{t}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{t}tan{h}'(W_{f}X_{t}+b_{f})$

　　假設$Z=tanh'(x)\sigma (y)$，則Z的函式影象如下圖所示：

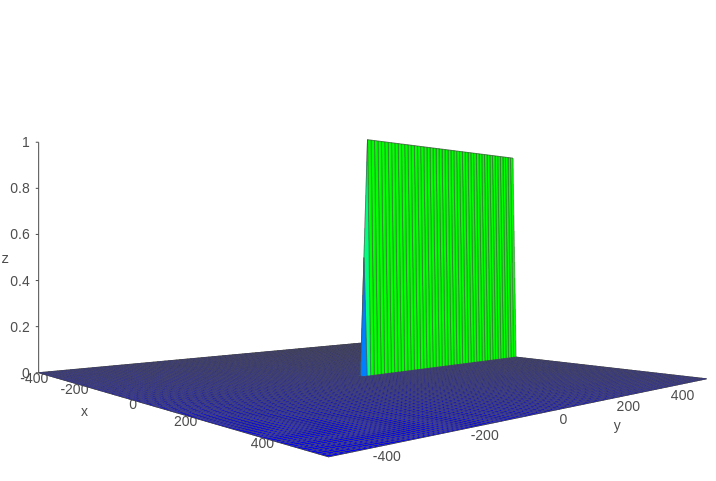
　　可以看到該函式值基本上不是0就是1。

　　傳統RNN的求偏導過程：

$\frac{\sigma L_{3}}{\sigma W}=\sum_{k=0}^{t}\frac{\partial L_{3}}{\partial o_{3}}\frac{\partial o_{3}}{\partial s_{3}}(\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}})\frac{\partial s_{k}}{\partial W}$

　　如果在LSTM中上式可能就會變成：

$\frac{\sigma L_{3}}{\sigma W}=\sum_{k=0}^{t}\frac{\partial L_{3}}{\partial o_{3}}\frac{\partial o_{3}}{\partial s_{3}}\frac{\partial s_{k}}{\partial W}$

　　因為$\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3}tan{h}'\sigma (W_{f}X_{t}+b_{f})\approx 0|1$，這樣解決了傳統RNN中梯度消失的問題。

參考

　　https://www.jiqizhixin.com/articles/2019-01-17-7

　　https://zhuanlan.zhihu.com/p/2868