Dijkstra演算法 c語言實現
阿新 • • 發佈:2019-01-08
Dijkstra(迪傑斯特拉)演算法是典型的最短路徑路由演算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止。Dijkstra演算法能得出最短路徑的最優解,但由於它遍歷計算的節點很多,所以效率低。
Dijkstra演算法是很有代表性的最短路演算法,在很多專業課程中都作為基本內容有詳細的介紹,如資料結構,圖論,運籌學等等。
其基本思想是,設定頂點集合S並不斷地作貪心選擇來擴充這個集合。一個頂點屬於集合S當且僅當從源到該頂點的最短路徑長度已知。
初始時,S中僅含有源。設u是G的某一個頂點,把從源到u且中間只經過S中頂點的路稱為從源到u的特殊路徑 ,並用陣列dist記錄當前每個頂點所對應的最短特殊路徑長度。Dijkstra演算法每次從V-S中取出具有最短特殊路長度的頂點u,將u新增到S中,同時對陣列dist作必要的修改。一旦S包含了所有V中頂點,dist就記錄了從源到所有其它頂點之間的最短路徑長度。
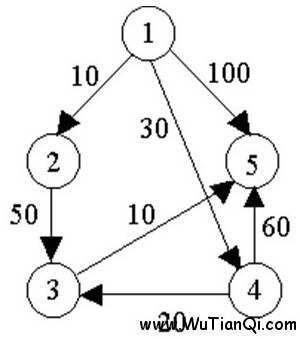
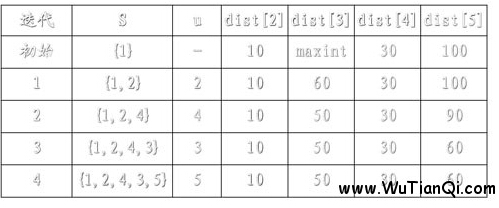
例如,對下圖中的有向圖,應用Dijkstra演算法計算從源頂點1到其它頂點間最短路徑的過程列在下表中。
Dijkstra演算法的迭代過程:
#include <stdio.h> #include <conio.h> #include <stdlib.h> #define X 10000 #define VertexNum 7 //實際上共有六個頂點(1---6) #define EdgeNum 9 int Graph[VertexNum][VertexNum] = //0 1 2 3 4 5 6 { X, X, X, X, X, X, X, //0 X, X, 6, 3, X, X, X, //1 X, X, X, X, 5, X, X, //2 X, X, 2, X, 3, 4, X, //3 X, X, X, X, X, X, 3, //4 X, X, X, X, 2, X, 5, //5 X, X, X, X, X, X, X //6 }; int Visited[VertexNum]; int path[VertexNum]; int Distance[VertexNum]; void Dijkstra(int Begin) { int MinEdge, Vertex, i,j, Edges; Edges = 1; Visited[Begin] = 1; for (i = 1; i<VertexNum; i++) Distance[i] = Graph[Begin][i]; Distance[Begin] = 0; printf(" 1 2 3 4 5 6\\n"); printf("-----------------------------------\\n"); printf("s:%d", Edges); for( i=1; i<VertexNum; i++) if (Distance[i] == X) printf(" *"); else printf("%3d",Distance[i]); printf("\\n"); while( Edges<VertexNum-1) { Edges++; MinEdge = X; for(j=1; j<VertexNum; j++) if (Visited[j]==0 && MinEdge > Distance[j] ) { Vertex = j; MinEdge = Distance[j]; } Visited[Vertex] = 1; printf("s:%d",Edges); for(j=1; j<VertexNum; j++) { if (Visited[j] == 0 && Distance[Vertex] + Graph[Vertex][j] <Distance[j]) { Distance[j] = Distance[Vertex] + Graph[Vertex][j]; path[j] = Vertex; } //printf("%6d",Distance[j]); if (Distance[j] == X) printf(" *"); else printf("%3d",Distance[j]); } printf("\\n"); } } void main() { int i; int k; // clrscr(); for(i=0; i<VertexNum; i++) { Visited[i] = 0; path[i] = 1;} Dijkstra(1); printf("\\n\\nAll Path-------------------------\\n"); for(i=2; i<VertexNum; i++) //printf("%5d",Visited[i]); { printf("[%d] ",Distance[i]); k = i; do { printf("%d<--",k); k = path[k]; } while (k!=1); printf("1 \\n"); } }
以上程式碼參考了資料結構課本
下面的是網上的程式碼:
以下是具體的實現(C/C++): /*************************************** * About: 有向圖的Dijkstra演算法實現 * Author: Tanky Woo * Blog: www.WuTianQi.com ***************************************/ #include <iostream> using namespace std; const int maxnum = 100; const int maxint = 999999; void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum]) { bool s[maxnum]; // 判斷是否已存入該點到S集合中 for(int i=1; i<=n; ++i) { dist[i] = c[v][i]; s[i] = 0; // 初始都未用過該點 if(dist[i] == maxint) prev[i] = 0; else prev[i] = v; } dist[v] = 0; s[v] = 1; // 依次將未放入S集合的結點中,取dist[]最小值的結點,放入結合S中 // 一旦S包含了所有V中頂點,dist就記錄了從源點到所有其他頂點之間的最短路徑長度 for(int i=2; i<=n; ++i) { int tmp = maxint; int u = v; // 找出當前未使用的點j的dist[j]最小值 for(int j=1; j<=n; ++j) if((!s[j]) && dist[j]<tmp) { u = j; // u儲存當前鄰接點中距離最小的點的號碼 tmp = dist[j]; } s[u] = 1; // 表示u點已存入S集合中 // 更新dist for(int j=1; j<=n; ++j) if((!s[j]) && c[u][j]<maxint) { int newdist = dist[u] + c[u][j]; if(newdist < dist[j]) { dist[j] = newdist; prev[j] = u; } } } } void searchPath(int *prev,int v, int u) { int que[maxnum]; int tot = 1; que[tot] = u; tot++; int tmp = prev[u]; while(tmp != v) { que[tot] = tmp; tot++; tmp = prev[tmp]; } que[tot] = v; for(int i=tot; i>=1; --i) if(i != 1) cout << que[i] << " -> "; else cout << que[i] << endl; } int main() { freopen("input.txt", "r", stdin); // 各陣列都從下標1開始 int dist[maxnum]; // 表示當前點到源點的最短路徑長度 int prev[maxnum]; // 記錄當前點的前一個結點 int c[maxnum][maxnum]; // 記錄圖的兩點間路徑長度 int n, line; // 圖的結點數和路徑數 // 輸入結點數 cin >> n; // 輸入路徑數 cin >> line; int p, q, len; // 輸入p, q兩點及其路徑長度 // 初始化c[][]為maxint for(int i=1; i<=n; ++i) for(int j=1; j<=n; ++j) c[i][j] = maxint; for(int i=1; i<=line; ++i) { cin >> p >> q >> len; if(len < c[p][q]) // 有重邊 { c[p][q] = len; // p指向q c[q][p] = len; // q指向p,這樣表示無向圖 } } for(int i=1; i<=n; ++i) dist[i] = maxint; for(int i=1; i<=n; ++i) { for(int j=1; j<=n; ++j) printf("%8d", c[i][j]); printf("\n"); } Dijkstra(n, 1, dist, prev, c); // 最短路徑長度 cout << "源點到最後一個頂點的最短路徑長度: " << dist[n] << endl; // 路徑 cout << "源點到最後一個頂點的路徑為: "; searchPath(prev, 1, n); } 輸入資料: 5 7 1 2 10 1 4 30 1 5 100 2 3 50 3 5 10 4 3 20 4 5 60 輸出資料: 999999 10 999999 30 100 10 999999 50 999999 999999 999999 50 999999 20 10 30 999999 20 999999 60 100 999999 10 60 999999 源點到最後一個頂點的最短路徑長度: 60 源點到最後一個頂點的路徑為: 1 -> 4 -> 3 -> 5 最後給出兩道題目練手,都是直接套用模版就OK的: 1.HDOJ 1874 暢通工程續 http://www.wutianqi.com/?p=1894 2.HDOJ 2544 最短路 http://www.wutianqi.com/?p=1892