本來打算自己寫寫的，但是發現了David Foster的神作，看了就懂了。我也就不說啥了。

看不清的話，原圖在後面的連線也可以找到。

沒懂？！！！那我再解釋下。

AlphaGo Zero主要由三個部分組成：自我博弈（self-play），訓練和評估。和AlphaGo 比較，AlphaZero最大的區別在於，並沒有採用專家樣本進行訓練。通過自己和自己玩的方式產生出訓練樣本，通過產生的樣本進行訓練；更新的網路和更新前的網路比賽進行評估。

在開始的時候，整個系統開始依照當前最好的網路引數進行自我博弈，那麼假設進行了10000局的比賽，收集自我博弈過程中所得到的資料。這些資料當中包括：每一次的棋局狀態以及在此狀態下各個動作的概率（由蒙特卡羅搜尋樹得到）；每一局的獲勝得分以及所有棋局結束後的累積得分（勝利的+1分，失敗得-1分，最後各自累加得分），得到的資料全部會被放到一個大小為500000的資料儲存當中；然後隨機的從這個資料當中取樣2048個樣本，1000次迭代更新網路

那麼我們首先來看一下AlphaZero的輸入的棋局狀態到底是什麼。如圖所示，是一個大小為19*19*17的資料，表示的是17張大小為19*19（和棋盤的大小相等）的特徵圖。其中，8張屬於白子，8張屬於黑子，標記為1的地方表示有子，否則標記為0 。剩下的一張用全1或者是全0表示當前輪到 黑子還是白子了。構成的這個資料表示遊戲的狀態輸入到網路當中進行訓練。

那麼我們來看一下，AlphaZero的網路到底是怎麼樣的呢？

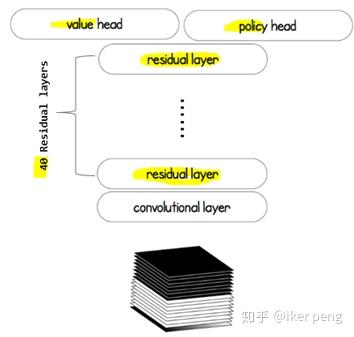
這個網路主要由三個部分組成：由40層殘差網路構成的特徵提取網路（身體），以及價值網路以及策略網路（兩個頭）。該網路當中價值網路所輸出的值作為當前的狀態的價值估計； 策略網路的輸出作為一個狀態到動作的對映概率。而這兩個部分的輸出都被引入到蒙特卡羅搜尋樹當中，用來指導最終的下棋決策。那麼顯然，價值網路輸出的是一個1D的標量值，在-1到1之間；策略網路輸出的是一個19*19*1的特徵圖，其中的每一個點表示的是下棋到該位置的概率。那我們來看一下，該網路是如何指導蒙特卡羅搜尋樹的。

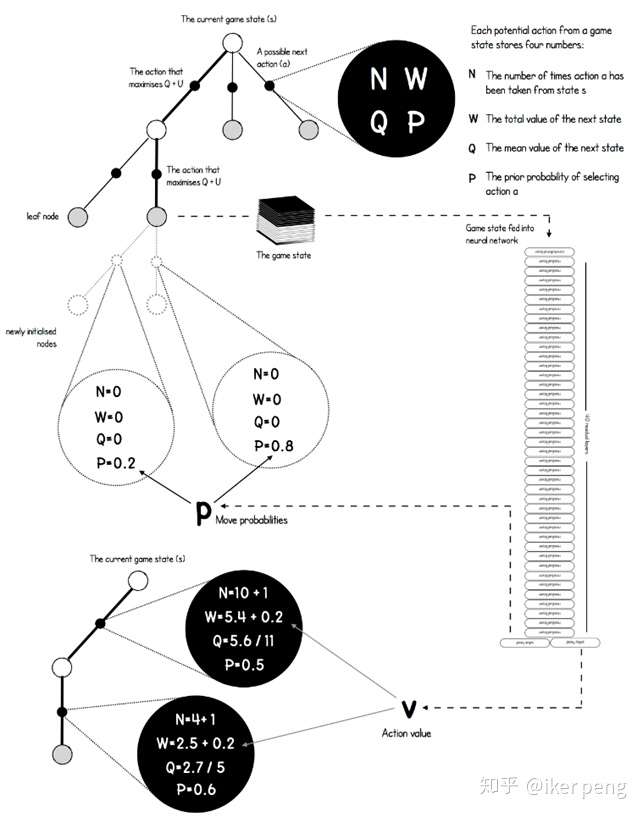
如圖所示，在圖中的搜尋樹當中，黑色的點表示的是從一個狀態過渡到另一個狀態的動作a；其餘的節點表示的是棋局的狀態，也就是之前所說的輸入。從一個非葉子節點的狀態開始，往往存在多種可能的行動，而其中的狀態節點a具有4種屬性，他們決定了到底應該如何選擇。具體來講，其中的N表示的是到目前為止，該動作節點被訪問的次數；P表示網路預測出來的選擇該節點的概率；W表示下一個狀態的總的價值，而價值網路輸出的動作的價值會被累及到這個值當中；這個值除以被訪問到的次數就等於平均的價值Q。實際上，還會給Q加上一個U來起到探索更多的動作的效果。我想應該是非常清楚的。那麼如何根據構建出來的搜尋樹進行下棋的步驟呢？在一定的閾值範圍內（比如說，1000個迭代之前），採用最大化Q函式的方式來選擇動作；那麼當大於這個閾值之後採用蒙特卡羅搜尋樹的方式（例如PUCT演算法，也就是根據概率和被訪問的次數）來選擇執行的動作。

那我們來看一下蒙特卡羅搜尋樹在這裡面時如何實現的。首先是其中的節點：

class Node:
    def __init__(self, parent=None, proba=None, move=None):
        self.p = proba
        self.n = 0
        self.w = 0
        self.q = 0
        self.children = []
        self.parent = parent
        self.move = move

其中主要為之前所說的4個屬性以及父子節點的指標。而最後一個move指出了在當前狀態下的合法下棋步驟。在訓練的過程中，這些值都會被更新，那麼在更新之後如何通過他們來進行動作的選擇呢？

def select(nodes, c_puct=C_PUCT):
    " Optimized version of the selection based of the PUCT formula "

    total_count = 0
    for i in range(nodes.shape[0]):
        total_count += nodes[i][1]
    action_scores = np.zeros(nodes.shape[0])
    for i in range(nodes.shape[0]):
        action_scores[i] = nodes[i][0] + c_puct * nodes[i][2] * \
                (np.sqrt(total_count) / (1 + nodes[i][1])) 
    equals = np.where(action_scores == np.max(action_scores))[0]
    if equals.shape[0] > 0:
        return np.random.choice(equals)
    return equals[0]

這裡表示的是對於任何一個節點，從其所有的子節點當中，通過PUCT演算法找出最大得分的那個節點。在這個得分action_scores[i]的計算過程中，網路預測的概率和該節點被訪問的次數都有被考慮。對於被訪問到的非葉子節點繼續進行擴充套件；而如果是葉子節點則進行最終的評估。至於其中的殘差網路模組，價值網路，策略網路就不再一一敘述了。詳細參考：

References: