數字影象處理- 3.6 銳化空間濾波器
3.6 銳化空間濾波器
銳化處理的主要目的是突出影象中的突出灰度的過度部分。總的來說，微分運算元的響應強度與影象在該店(應用了運算元)的突變程度有關。這樣一來，影象微分增強了邊緣和其他突變(如噪聲)並削弱了灰度變化緩慢的區域。
為了說明簡單，主要集中討論一階微分的性質。我們最高興去的微分性質是恆定灰度區域(平坦段)、突變的開頭與結尾(階梯和斜坡突變)及沿著灰度級斜坡處的特性。這些型別的突變可以用來對影象中的噪聲點、細線與邊緣模型化。
3.6.1 基礎
數字函式（影象，離散的數字序列）的微分定義條件：
這裡我們首先了解下數學函式的微分，微分可以用不同的術語定義，也有各種方法定義這些差別，然而，對於一階微分任何定義都必須保證以下幾點：
(1)在平坦段(灰度不變區域)微分值為零；
(2)在灰度階梯或斜坡的起始點處微分值非零；
(3)沿著斜坡面微分值非零。
任何二階微分的定義也類似：
（1）在平坦去微分值必為零；
（2）在灰度階梯或斜坡的起始點處微分值非零；
（3）沿著斜坡面微分值非零。
因為我們處理的是數字量，其值是有限的，故最大灰度級的變換也是有限的，變化發生最短距離是在兩相鄰畫素之間。
對於一元函式f(x)表達一階微分定義是一個差值：
∂f/∂x = f(x+1) − f(x)
二階導數：(∂f/∂x)/∂x = f(x+2) - f(x+1) -f(x+1)+f(x)
相當於：f(x+1)-2f(x)+f(x-1)
這裡，為了與對二元影象函式f(x,y)求微分時的表示式保持一致，使用偏導數符號，對二元函式，我們將沿著兩個空間軸處理偏微分，類似地，用差分定義二階微分：
下圖表明瞭上述的具體含義。
注意下圖中二階差分的零交叉點（Zero crossing），零交叉點對於邊緣的定位非常有用。
由於影象邊緣處的一階微分是極值點, 影象邊緣處的二階微分應為零,確定零點的位置要比確定極值點更容易,也更準確"
我們發現交叉點就是邊緣，而一階微分中卻沒有這樣的性質
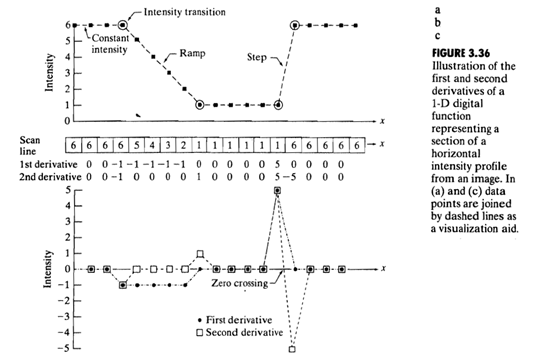
二階微分在增強細節方面比一階微分好得多，這是一個適合銳化影象的理想特徵。
3.6.2 基於二階微分的影象增強--拉普拉斯運算元
這裡介紹二階微分在影象增強處理中的應用。
首先定義一個二階微分的離散公式，然後構造一個基於此式的濾波器。
我們最關注的是一種各向同性濾波器，這種濾波器的響應與濾波器作用的影象的突變方向無關。
也就是說，各向同性濾波器是旋轉不變的，即將原始影象旋轉後進行濾波處理給出的結果與先對影象濾波，然後再旋轉的結果相同。
處理方法
最簡單的各向同性微分運算元是拉普拉斯運算元，一個二元影象函式f(x,y)的拉普拉斯變換定義為：
因為任意階微分都是線型操作，所以拉普拉斯變換也是一個線性操作。
考慮到有兩個變數，因此，我們在x，y方向上對二階偏微分採用下倆定義：
因此二維拉維拉斯數字實現可由這兩個分量相加得到：
，
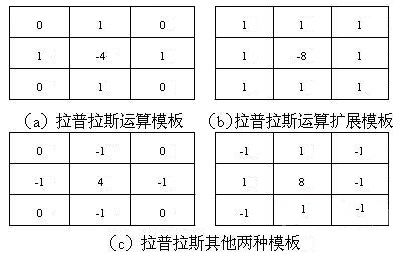
這裡關注係數矩陣即掩膜：
這個矩陣給出了在90度方向上旋轉的各向同性結果，如果向得到45度方向上旋轉的各向同性結果則，將中心對角點標為1，中心點為-8即可。
由於拉普拉斯是一種微分運算元，它的應用強調影象中灰度的突變及降低灰度慢變化的區域。將原始影象和拉普拉斯影象疊加在一起的簡單方法可以保護拉普拉斯銳化處理的效果，同時又能復原背景資訊。我們使用拉普拉斯變換對影象增強的基本方法可表示為下式：
含有對角線資訊的拉普拉斯運算元
3.6.3 非銳化掩蔽和高提升濾波
在印刷和出版界用了多年的影象銳化處理過程，從原圖中減去一副非銳化（平滑後的）影象，達到銳化的目的。
步驟有以下幾步：
- 模糊源影象
- 從原影象中減去模糊影象（產生的差值影象稱為模板）
- 將模板加到原影象上。
令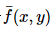 
表示模糊影象，那麼首先我們得到模板：
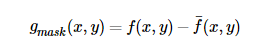
然後在原影象上加上該模板的一個權重部分：
上式中，當k=1時，我們得到上面定義的非銳化掩蔽，當k>1時，該處理稱為高提升濾波，當k<1時，則不強調非銳化模板的貢獻。
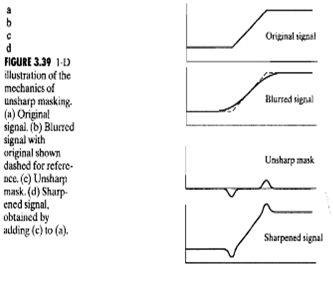
需要注意的是，如果k足夠大的時候，負值將導致邊緣周圍有暗的暈輪，會產生不好的效果。
3.6.4 使用一階微分對（非線性）影象銳化—梯度
一個函式f在f(x,y)的梯度是定義為二維列向量（這是一個向量，給定了一個方向）：
然後其幅度值為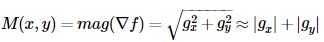
，其中M(x,y)是與原影象大小相同的影象，該影象通常稱為梯度影象。後面的表示式仍保留了灰度的變換，但丟失掉了其各向同性。
下面介紹兩種運算元：一階Roberts交叉梯度運算元和二階Soble運算元：
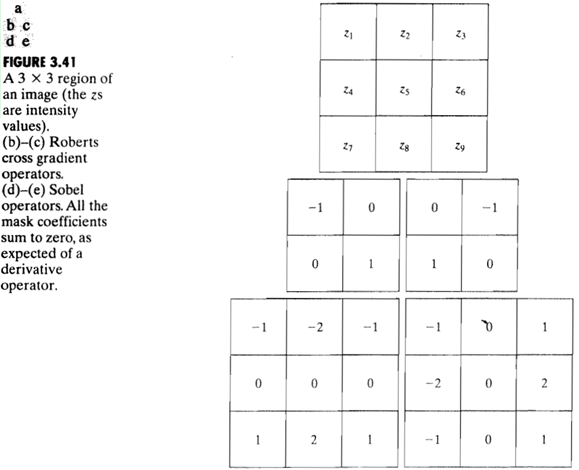
在3×3的區域影象中，應該是gx = (z8−z5) gy = (z9−z6),但是Roberts進行了改良，提出了Roberts運算元，gx=(z9−z5)，gy=(z8−z6)；
由於偶數模板沒有對稱中心，所以與之前的卷積模板定義中，運算結果等會中心點位置值不能對應， 所以使用奇數的模板，例如3 * 3 的Soble運算元，gx=(z7+2z8+z9)−(z1+2z2+z3)，gy=(z3+2z6+z9)−(z1+2z4+z7)。
使用梯度進行邊緣增強，可以用以突出灰度影象中看不見的小斑點，在下面的例子中甚至可以去除灰度不變或變換緩慢的圖案陰影。
3.7 混合空間增強法
本書所提供例子的策略是：用Laplace突出影象中的小細節，然後使用梯度法突出邊緣。
平滑過得梯度影象用於掩蔽Laplace影象，最後使用灰度變換來增大影象的灰度動態範圍。
其中降低噪聲可以使用中值濾波器或者使用原影象梯度操作的平滑形式形成的一個模板。
影象請直接參考Digital Image Processing （3rd Edition）Page 192。
3.8 使用模糊技術進行灰度變換和空間變換
3.8.1 引言
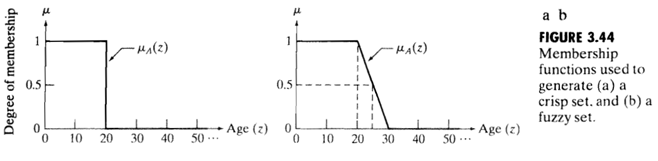
隸屬度函式μ(z)：用以描述一個元素是否屬於集合的模糊程度，若是一個階躍函式，可以認為是一個我們所瞭解的"乾脆的"集合，若是一個分段函式，則可以看做一個模糊集合：
3.8.2模糊集合論原理
模糊集合是一個有z值和（賦予z成員等級的）相應隸屬度函式組成的序對，即
A={z,μA(z)|z∈Z}
其中隸屬度函式是關鍵，表明了元素z到集合的一種對應關係。
如果隸屬度函式僅有0,1兩個值，那麼模糊集合退化為"乾脆的"集合。
下面這張圖展示了模糊集合間的一些關係：
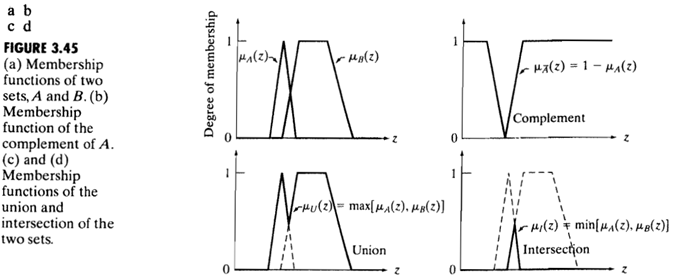
有一些常用的隸屬度函式，如三角形、梯形、∑型、S型、種型、截尾高斯型等，之後用到了會另作介紹。
3.8.3 模糊集合的應用（略）
3.8.4 使用模糊集合進行灰度變換
對於一副灰度影象，描述它的某個區域"暗的"、"灰的"、"亮的"都是利用模糊的概念，那麼我們將給予這三種情況定義三種模糊集合：
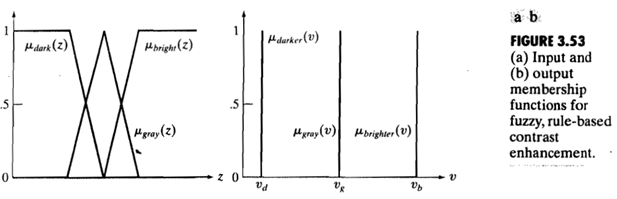
那麼對於任何輸入z0，輸出v0為
從書中給予的例子中來看，影象的細節部分得到了比較好的保留，但代價是計算量大大增加。
寫在最後：既然是為了達到銳化的目的，就是保留影象固有的邊緣特性,那麼在影象還原（插值）的操作中，這些濾波器仍然可以使用。而且能夠保持原有影象的邊緣特點。
1，直接使用可以保留邊緣特性的mask進行插值。
2.利用銳化用使用的邊緣檢測演算法對邊緣求解，然後分別處理邊緣區域 和 非邊緣區域。