數字影象處理- 3.4 空間濾波 and 3.5 平滑空間濾波器
3.4 空間濾波基礎
• Images are often corrupted by random variations in intensity, illumination, or have poor contrast and can’t be used directly.
• Filtering: transform pixel intensity values to reveal certain image characteristics
– Enhancement: improves contrast – Smoothing: remove noises – Template matching: detects known patterns.
影象經常被強度、光照的隨機變化損壞,或者對比度差,不能直接使用。
濾波:對畫素強度值進行變換,以顯示一定的影象特徵
-增強:增強對比度
-平滑:去除噪聲
-模板匹配:檢測已知模式。
空間濾波器:由一個鄰域(典型是個小矩形)及其所涵蓋的影象畫素執行預定義操作組成。
濾波產生的新畫素座標 等於 鄰域中心的座標。
濾波(filtering)一詞是借用頻域處理中的詞彙,是指接受或者拒絕一定的頻率分量,。
例如,通過低頻的濾波器稱為低通濾波器。
What is a mask
A mask is a filter. Concept of masking is also known as spatial filtering. Masking is also known as filtering. In this concept we just deal with the filtering operation that is performed directly on the image.
-masking 是 指在image 領域的 filtering。
什麼是面具
蒙版是一個過濾器。
掩蔽的概念也稱為空間過濾。掩蔽也稱為濾波。在這個概念中,我們只處理直接對影象執行的濾波操作。
What is filtering
The process of filtering is also known as convolving a mask with an image. As this process is same of convolution so filter masks are also known as convolution masks.
-filtering 是 mask 與 image 進行卷積操作,所以mask 又叫 卷積掩膜。
什麼是過濾
濾波的過程也稱為掩碼與影象的卷積。
因為這個過程和卷積是一樣的所以濾波掩碼也被稱為卷積掩碼。
總結:filtering 是訊號鄰域的詞彙,用來消除隨機產生的噪聲或者加強訊號的特點。
當傳到digital image processing(DIP)領域以後,也可以叫masking。
而濾波也好,masking 也罷,本質上都是卷積操作,或者是相關操作。
3.4.1 空間濾波機理
- 如果在影象畫素上執行線性操作,那該濾波器稱為線性濾波器
- 否則稱為非線性濾波器

空間濾波的機理示於圖3.32。
該處理就是在待處理影象中逐點地移動掩模。在每一點(x,y)處,濾波器在該點的響應通過事先定義的關係來計算。
對於線性空間濾波(見2.6節線性的定義),其響應由濾波器係數與濾波掩模掃過區域的相應像索值的乘積之和給出。
圖3.32所示為3×3的掩模,在影象中的點(x,y)處,用該掩模線性濾波的響應R為:
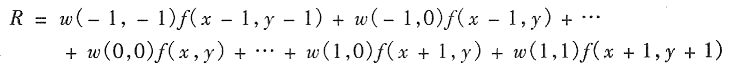
我們看到的是掩模係數與直接在掩模下的相應畫素的乘積之和。
注意,具體地說,係數ω(0,0)與影象值f(x,y)相符合是指當乘積求和計算髮生時,掩模位於(x,y)的中心。
對於一個尺寸為m×n的掩模,我們假設m=2a十1且n=2b+l,這裡a,b為非負整數。
即,在後續的討論中,處理的掩模的長與寬都為奇數,其有意義的最小尺寸3×3(在我們的討論中排除了無足輕重的1×1掩模)。
一般來說,在M×N的影象f上,用m×n大小的濾波器掩模進行線性濾波由下式給出:

3.4.2 空間相關(Correlation)與卷積(Convolution)操作
寫在前面:(按照訊號卷積的理論,N維向量與M維向量卷積後,所得向量的長度為:N+M。與我們後面要討論情形的有所不同,請注意區分。)
一維:
為了便於理解,我們先引入一維函式濾波的概念,再引入二維影象的濾波。
基本原理:濾波器w與函式f起始位置對齊後,逐位移動,並且每次移動都進行按位相乘結果累加得到某位的結輸出。
設,一維函式 f 為: 0 0 0 0 1 0 0 0 0 ; 濾波器 w:1 2 3 4 5
相關運算的過程:
1、對齊:將 w 的開始位置 5 與 f 的開始位置 0對齊。對齊位置作為運算起點。
2、填充:為了使得 w 每一次運算中各位都有值相乘,對 f 起始位置和結尾無對應位的位置進行“0填充”。
(注意下填充的概念,在影象濾波中,填充的值對影象濾波的影響比較大。)。
3、 計算:將上下對應的位相乘後全部相加得到結果的第一位,輸出位置總是在。
向右移動濾波器w “N”位,並進行相同的運算得到相應第N位的計算結果。
4、 輸出大小: Matlab中我們使用imfilter函式來進行卷積或者相關運算;(後文中,將具體介紹imfilter函式。)
得到的結果的大小分為“full”和“same”兩類,full包含填充項,same為原f大小。
卷積運算與相關運算類似,只是將濾波器矩陣旋轉了180°後進行與之一樣的運算。
二維:
一維和二維的情況很相像,需要注意填充擴充套件對影象的影響,我們將在後面的實驗中討論。
總的來說:從開始位置平移掩膜到第一行執行結束位置,在每個位置上執行掩膜覆蓋的亮度值與對應的掩膜係數相乘結果累加得到對應點的畫素值。
然後跳到第二行的起始位置繼續平移和運算,如此反覆直到掩膜移動到 整個運算的結束位置。
(不過根據設定輸出影象大小為same還是full,掩膜移動的範圍有所不同。後文將講具體描述。)
關於掩膜的大小:通常使用奇數維的方陣作為掩膜/濾波器,因為奇數維的方正有唯一的一箇中心點,比較直觀。
相關運算:
1、對齊:得到same大小的輸出結果,只需要保證掩膜中心能夠覆蓋全圖每個畫素點即可。
此時只需將掩膜中心與影象矩陣第一行第一個元素對齊即可。
full 的情況如下圖,得到的有值的區域可能會有所拓寬,不過不影響原圖大小尺寸的濾波結果的得出。
2、填充:同一維中的理由,在二維中我們需要對影象進行填充。
Matlab中的填充方式有4種:
a/ 通過值P來進行擴充套件。(P為常量值,如本例中使用的為“0”)
b/ 過複製影象邊界進行擴充套件填充。
c/ 過映象反射影象邊界來擴充套件填充。d/ 影象看成二維周期函式來擴充套件。
在函式imfilter中會有具體的引數來設定這幾種方式。後面函式介紹部分會具體描述。
3、運算:將掩膜覆蓋的亮度值與對應的掩膜係數相乘後結果累加得到對應點的輸出畫素值。然後進行平移繼續運算,如此反覆,直到平移結束位置。
4、輸出大小:分為full 型別和same型別。其意義與一維中一致。
卷積運算的情況與相關類似,不過對掩膜進行了180°的旋轉。
公式表示:w表示模板,f表示影象
 |
 |
| 模板 mask | 影象 |
注:(s,t)指的是該點距離 當前中心畫素點 的相對位置
上面的公式是表示相關,應該用空心的五角星,但是沒找到。 w和f是對應位置相乘。
上面的公式表示卷積,是實心的五角星。 w和f的轉置的對應位置相乘。
3.4.3 線性濾波器的向量表示
3.4.4 空間濾波器的模板的產生
生成一個大小為m*n的線性空間濾波器要求制定mn個模板係數,這些係數是根據所要求的操作得到的。例如,我們想把影象中的像值替換為以這些點為中心點的,3*3的領域的平局灰度代替。 就出現了平均模板:
在某些應用中,我們有一個具有兩個變數的連續函式,其目的是得到一個空間濾波模板。例如:有兩個變數的高斯函式的基本形式如下:
delte是標準差,控制二維高斯函式鐘形的“緊度”。通常我們設座標x,y是整數(影象的畫素座標),如果想用這個二元函式生成3*3的模板,那麼就關於其中心進行取樣。
這樣,就有。 如下圖所示:

3.5 平滑空間濾波器
平滑線性濾波器,也叫均值濾波器,是低通濾波器( 因為這樣的操作降低了灰度的‘尖銳’變化)
- 所有係數都相等的濾波器,可以看出是求模板內畫素的平均值
- 加權平均模板,根絕不同位置設定不同權重,如下圖,權重隨距離增加遞減。對角線位置距離比直接接觸的距離大,所以權重變為1。按照1/2的等比隨著距離增加進行遞減。重要:這個模板的目的是 在平滑處理中降低模糊

統計排序(非線性)濾波器
以濾波器包圍的影象區域中包含的畫素的排序為基礎,然後使用統計排序結果決定代替中心的畫素值。最知名的叫 中值濾波器,這種濾波器對脈衝噪聲非常有效,也稱為椒鹽噪聲。
分析: 因為濾波器用統計中的數列中值代替模板中心位置處的值,這樣就比均值更加保證了銳度的特點。
使得擁有不同灰度的點看起來更接近於它的相鄰點。
注:既然是統計特性決定的輸出,可以取50%處的值,也可以取最小值,最大值等等其他的統計特性。


===========補充閱讀
1. In image processing, a kernel, convolution matrix, or mask is a small matrix useful for blurring, sharpening, embossing, edge-detection, and more. This is accomplished by means of convolution between a kernel and an image.
2. Image Filtering in the Spatial Domain。
Filtering is a technique for modifying or enhancing an image. For example, you can filter an image to emphasize certain features or remove other features. Image processing operations implemented with filtering include smoothing, sharpening, and edge enhancement.
Filtering is a neighborhood operation, in which the value of any given pixel in the output image is determined by applying some algorithm to the values of the pixels in the neighborhood of the corresponding input pixel. A pixel's neighborhood is some set of pixels, defined by their locations relative to that pixel. (SeeNeighborhood or Block Processing: An Overview for a general discussion of neighborhood operations.) Linear filtering is filtering in which the value of an output pixel is a linear combination of the values of the pixels in the input pixel's neighborhood.




